Полная энергия частицы движущейся жидкости
Как известно из механики, тело, находящееся в покое или в движении, обладает определенным запасом механической энергии, который характеризуется двумя величинами: потенциальной энергией и кинетической энергией.
Потенциальной энергией Eп в поле сил тяжести является произведение веса тела P (частицы жидкости) на высоту его поднятия z, отсчитываемую от некоторой условной горизонтальной плоскости
Eп = P · z = mgz, (8.1)
где m – масса частицы.
Кинетическая энергия Eк равняется половине произведения массы тела (частицы жидкости) на квадрат ее скорости
Eк = 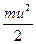 . (8.2)
. (8.2)
В механике жидкости следует учитывать также потенциальную энергию, обусловленную упругим состоянием, проявляющуюся в том, что, например, находящийся под давлением газ или пар обладает способностью при расширении совершать механическую работу; жидкости также обладают определенной сжимаемостью. Запас этой так называемой потенциальной энергии состояния Eп.с. тем больше, чем больше объем жидкости и чем выше давление, и определяется зависимостью
Eп.с. = pW, (8.3)
где p – давление; W = 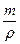 =
= 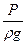 – объем тела (частицы жидкости).
– объем тела (частицы жидкости).
Таким образом, полная механическая энергия частицы жидкости равна
E = mgz + pW + 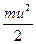 . (8.4)
. (8.4)
Энергия, отнесенная к единице веса частицы жидкости, называется удельной энергией;деля (8.4) на вес частицы жидкости P = mg = Wρg, получим для удельной энергии e выражение
e = z + 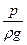 +
+ 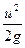 , (8.5)
, (8.5)
где составляющая z представляет собой удельную потенциальную энергию положения, составляющая 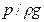 – удельную потенциальную энергию состояния и
– удельную потенциальную энергию состояния и 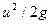 – удельную кинетическую энергию.
– удельную кинетическую энергию.
В большинстве инженерных гидравлических расчетов необходимо знать давление или среднюю скорость. При этом очевидно, что на величины скорости и давления не влияет массовый расход всего потока – проще говоря, давление может быть очень большим в тонкой трубке при малом расходе и может быть малым в потоке, переносящем десятки кубических метров жидкости в секунду (аналогичные замечания справедливы и для скорости). Поэтому для определения давления p и скорости u достаточно выражения для удельной энергии в виде (8.5), а основные расчеты проводятся в терминах удельной энергии - 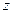 , p/
, p/ 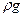 и u2/
и u2/ 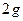 .
.

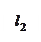
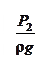
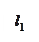
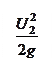
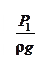
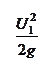
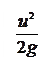
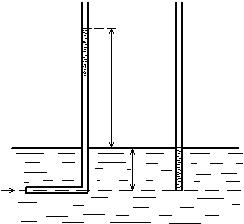
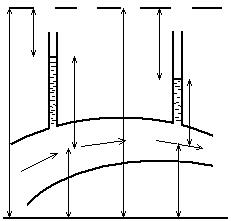
Рис. 8.1 Рис. 8.2
Все составляющие удельной энергии имеют размерность длины и называются так: z – геометрическая высота; 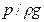 – пьезометрическая высота;
– пьезометрическая высота; 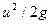 – высота скоростного напора.
– высота скоростного напора.
Из механики известно, что тело, брошенное вертикально вверх с начальной скоростью V, поднимается, если пренебречь сопротивлением среды, на высоту
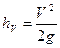 .
.
Пусть в потоке жидкости изогнутая открытая с обоих концов стеклянная трубочка помещена так, что одно колено трубки направлено навстречу течению, а второе расположено вертикально (рис. 8.1); опыт показывает, что жидкость во втором колене поднимается над уровнем, соответствующим поверхности потока, на высоту 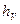 .
.
Если рядом с этой трубкой погрузить на ту же глубину другую, неизогнутую и также открытую с обоих концов, поместив ее в той же вертикальной плоскости, то жидкость в ней установится на одном уровне с поверхностью потока; обозначив давление в точке, соответствующей глубине погружения обеих трубок, через 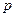 , найдем, что по отношению к этой точке уровень в изогнутой трубке находится на высоте
, найдем, что по отношению к этой точке уровень в изогнутой трубке находится на высоте
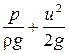 ,
,
в то время как в прямой трубке – на высоте 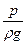 , так что разность высот в трубках
, так что разность высот в трубках 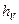 будет равна высоте скоростного напора.
будет равна высоте скоростного напора.
На примере сужающегося потока (рис. 8.2) поясним смысл каждой составляющей полной механической энергии и смысл выражения (8.5):
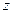 – геометрическая высота, т.е. расстояние по вертикали от оси сравнения О – О до центра тяжести сечения потока,
– геометрическая высота, т.е. расстояние по вертикали от оси сравнения О – О до центра тяжести сечения потока, 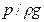 – высота столба жидкости в пьезометре,
– высота столба жидкости в пьезометре, 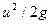 – удельная кинетическая энергия. Сумма этих высот дает полную механическую энергию.
– удельная кинетическая энергия. Сумма этих высот дает полную механическую энергию.
Дата добавления: 2016-08-23; просмотров: 2516;











