Сила избыточного суммарного давления жидкости на плоскую фигуру равна произведению площади фигуры S на избыточное давление в ее центре тяжести.

Это правило остается справедливым и для полного суммарного давления, т.е. при учете давления на свободной поверхности жидкости р₀. В этом случае

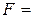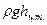( р₀₊ )S. (7.20)

Центр давления. Точка, в которой приложена равнодействующая гидростатического давления жидкости на плоскую площадку, называется центром давления.

Расстояние вдоль стенки от свободной поверхности до центра давления l_ц.д. равно

l_ц.д.=l_ц.т.+ ,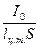

где I₀ – момент инерции рассматриваемой фигуры относительно оси, проходящей через ее центр тяжести. Последняя формула показывает, что центр давления расположен ниже центра тяжести. Для вертикальной, прямоугольной плоской стенки высотой h и шириной b (глубина воды h)

h_ц.т.= 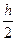, h_ц.д.= 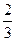h. (7.21)

Задача 7.7.Подпорная вертикальная прямоугольная стенка шириной В=10 м сдерживает напор воды высотой Н=1,5 м. Определить силу избыточного давления F на стенку. Плотность воды принять 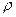=1000 кг/м³.

Решение. Силу F избыточного давления определяем по формуле (7.19), площадь на которую действует давление, равна 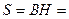10∙1,5=15 м². Так как стенка прямоугольная, то ее центр тяжести находится в точке пересечения диагоналей и глубина погружения его под поверхностью воды равна h_ц.т.=0,75 м. Окончательно величина силы F равна

F=1000∙9,8∙0,75∙15=110250 Н.

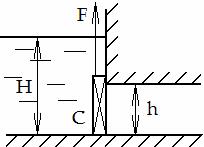
Рис. 7.21 Задача 7.8.Определить силу F, необходимую для подъема щита С, закрывающего прямоугольное отверстие высотой h=3 м и шириной В=4 м (рис. 7.21). Напор воды перед щитом H=5 м, коэффициент трения в направляющих щита при подъеме f=0,03, вес щита 500 кг.