Игра 2–х лиц без седловой точки. Смешанные стратегии
Одна из возможностей расширения стратегий игроков – разнообразить способ выбора своей стратегии, например, «случайно».
Как мы уже отмечали, в отсутствии Седловой точки, игрок А, применяя свою максиминную стратегию, выиграет не менее  , а игрок В, применяя свою минимаксную стратегию, проигрывает не более
, а игрок В, применяя свою минимаксную стратегию, проигрывает не более  , где
, где  . Применение чистых стратегий в каждой партии такой игры не дает возможность игрокам увеличить выигрыш
. Применение чистых стратегий в каждой партии такой игры не дает возможность игрокам увеличить выигрыш 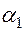 , чем уменьшить проигрыш
, чем уменьшить проигрыш  . Для того, чтобы это было возможным необходимо применять не одну, а несколько чистых стратегий, чередуя их случайным образом с какими–то частотами. Такая стратегия получила название смешанной (ее элементами являются чистые стратегии).
. Для того, чтобы это было возможным необходимо применять не одну, а несколько чистых стратегий, чередуя их случайным образом с какими–то частотами. Такая стратегия получила название смешанной (ее элементами являются чистые стратегии).
Смешанная стратегия имеет смысл при условии, что игра состоит более чем из одной партии.
Обозначим смешанные стратегии игроков А и В через
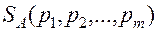 и
и 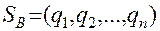 , где
, где
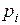 – вероятность (частота) применения игроком А чистой стратегии
– вероятность (частота) применения игроком А чистой стратегии 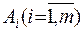 ,
, 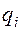 – вероятность (частота) принятия игроком В чистой стратегии
– вероятность (частота) принятия игроком В чистой стратегии 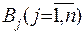 .
.
Причем  и
и 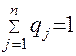 .
.
Чистые стратегии игроков А и В, для которых вероятности 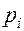 и
и 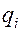 отличны от 0, называются активными.
отличны от 0, называются активными.
Теорема (основная теорема теории игр) (теорема минимакса).
Любая конечная игра двух лиц с нулевой суммой имеет, по крайней мере, одно решение (т.е. пару оптимальных стратегий, в общем случае смешанных) и соответствующую цену.
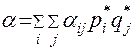
Решение игры, не имеющей Седловой точки, может осуществляться различными методами. Рассмотрим наиболее важные из них.
7.3.1. Графическое решение игр вида (2×n) и (m×2)
Этот метод применим только к играм, в которых хотя бы один игрок имеет только две стратегии.
Рассмотрим следующую игру (без Седловой точки)



Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, представлены в таблице
| В А | 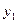
| 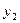
| … | 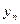
|

| 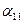
| 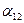
| … | 
|

| 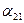
| 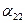
| … | 
|
Отсюда видно, что ожидаемый выигрыш игрока А линейно зависит от  . В соответствии с критерием минимакса игрок А должен выбирать
. В соответствии с критерием минимакса игрок А должен выбирать  так:
так:
| Чистые стратегии игрока В | Ожидаемые выигрыши игрока А |

| |

| |
| … | … |
| N | 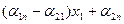
|
Пример:
| Вj Аi | В1 | В2 | В3 |
| ||
| А1 |   6 6
| |||||
| А2 | ||||||
| А3 | ||||||
| А4 |
Замечания: Стратегии, для которых есть доминирующие и дублирующие стратегии можно отбрасывать.
| Вj Аi | В1 | В2 | В3 | В4 |
| А1 | ||||
| А4 |
|

| Вj Аi | В1 | В2 | В4 | |
| А1 | ||||
| А4 | ||||

| Чистая стратегия Игрок В | Ожидаемый выигрыш игрока А | 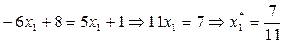
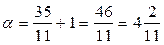 – цена игры – цена игры

| ||
| –6х1 + 8 | ||||
| –2х1 + 6 | ||||
| 5х1 + 1 | ||||
| Чистая стратегия Игрока А | Ожидаемый выигрыш Игрока В | 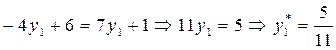
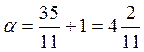
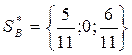
| |
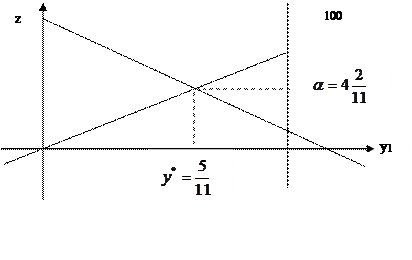
| –4у1+6 | |||
| 7у1+1 | |||
 |
7.3.2. Решение игр “m×n” симплекс–методом
Допустим, что все элементы платежной матрицы 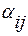 положительны. Этого можно добиться, добавив ко всем членам матрицы достаточно большое число М. Это приведет к увеличению цены игры
положительны. Этого можно добиться, добавив ко всем членам матрицы достаточно большое число М. Это приведет к увеличению цены игры 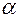 на М, а оптимальное решение
на М, а оптимальное решение 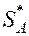 и
и  не изменится.
не изменится.
| B A | q1 | q2 | … | qn |
| p1 | α11 | α12 | … | α1n |
| p2 | α21 | α12 | … | α2n |
| … | … | … | … | … |
| pm | αm1 | αm2 | … | αmn |
Найдем сначала 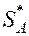 . На основе принципа целесообразности.
. На основе принципа целесообразности.
 или
или
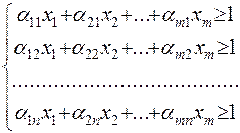
где 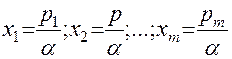
Очевидно: 
Таким образом, решение игры свелось к следующей задаче
 (1) – это задача линейного программирования
(1) – это задача линейного программирования
Оптимальная стратегия игрока В находится аналогично. Она является решением задачи.
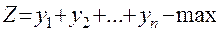

 (2)
(2)

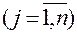
Нетрудно видеть, что задачи (1) и (2) – пара двойственных задач. Следовательно,  .
.
Дата добавления: 2020-11-18; просмотров: 751;











