Импеданс тканей организма. Дисперсия импеданса. Физические основы реографии
Ткани организма проводят не только постоянный (см. § 12.10), но и переменный ток. Опыт показывает, что в этом случае сила тока, проходящая через биологическую ткань, опережает по фазе приложенное напряжение. Следовательно (см. § 14.3), емкостное сопротивление тканей больше индуктивного. В таблице 24 в качестве примера приведены значения разности фаз тока и напряжения для некоторых тканей (частота 1 кГц).
Таблица 24
| Название ткани | Фаз в градусах |
| Кожа человека, лягушки | -55 |
| Нерв лягушки | -64 |
| Мышцы кролика | -65 |
Отсюда следует, что моделировать электрические свойства биологических тканей можно, используя резисторы, которые обладают активным сопротивлением, и конденсаторы — носители емкостного сопротивления. В качестве модели обычно используют эквивалентную электрическую схему тканей организма. Она представляет собой схему, состоящую из резисторов и конденсаторов, частотная зависимость (дисперсия) импеданса которой близка к частотной зависимости импеданса биологической ткани.
 На рис. 14.10 представлен график частотной зависимости импеданса мышечной ткани. Ради компактности кривая построена в логарифмических координатах. Из графика видны две особенности этой зависимости: во-первых, плавное уменьшение импеданса с увеличением частоты (общий ход зависимости импеданса от частоты) и, во-вторых, наличие трех областей частот, в которых имеет место отклонение от общего хода зависимости импеданса от частоты: Z мало изменяется. Они были названы, соответственно, областями α-, (β- и γ-дисперсии импеданса.
На рис. 14.10 представлен график частотной зависимости импеданса мышечной ткани. Ради компактности кривая построена в логарифмических координатах. Из графика видны две особенности этой зависимости: во-первых, плавное уменьшение импеданса с увеличением частоты (общий ход зависимости импеданса от частоты) и, во-вторых, наличие трех областей частот, в которых имеет место отклонение от общего хода зависимости импеданса от частоты: Z мало изменяется. Они были названы, соответственно, областями α-, (β- и γ-дисперсии импеданса.
 Установим, какая электрическая схема (модель) наиболее удачно отражает общий ход зависимости импеданса ткани организма от частоты. В качестве вариантов рассмотрим схемы, представленные на рис. 14.11.
Установим, какая электрическая схема (модель) наиболее удачно отражает общий ход зависимости импеданса ткани организма от частоты. В качестве вариантов рассмотрим схемы, представленные на рис. 14.11.
Для схемы, изображенной на рис. 14.11, а, частотная зависимость импеданса может быть получена из (14.41) при L = 0:
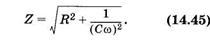
В соответствии с формулой (14.45) импеданс уменьшается с увеличением частоты, однако име-
ется противоречие с опытом: при ω→∞ Z →∞. Последнее означает бесконечно большое сопротивление при постоянном токе, что противоречит опыту (рис. 14.10).
Схема, изображенная на рис. 14.11, б, соответствует общей тенденции экспериментальной кривой: при увеличении частоты уменьшается емкостное сопротивление и уменьшается импеданс. Однако при ω →∞,Хс →0 и Z → 0, что не соответствует опыту.
Наиболее удачна схема рис. 14.11, в, в ней отсутствуют противоречия с опытом, характерные для двух предыдущих схем. Именно такое сочетание резисторов и конденсатора может быть принято за эквивалентную электрическую схему тканей организма. Частотная зависимость импеданса эквивалентной электрической схемы соответствует общему ходу экспериментальной зависимости импеданса от частоты. Важно отметить, что при этом электроемкость и, следовательно, диэлектрическая проницаемость остаются постоянными.
Поясним причину возникновения областей α-, β- и γ-дисперсии импеданса. Ткань организма является структурой, обладающей свойствами проводника (электролита) и диэлектрика. Поляризация диэлектрика (§ 12.6) во внешнем электрическом поле происходит не мгновенно, а зависит от времени. Это означает зависимость от времени поляризованности диэлектрика (Ре) при воздействии постоянного . электрического поля (Е — напряженность электрического поля):
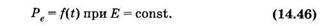
Если электрическое поле изменяется по гармоническому закону, то поляризованность будет также изменяться по гармоническому закону, а амплитуда поляризованности будет зависеть от частоты изменения поля с запаздыванием по фазе:
 |
Из (12.41) получим выражение для диэлектрической проницаемости:
Из (14.48) следует, что условие (14.47) означает частотную зависимость диэлектрической проницаемости при воздействии переменным (гармоническим) электрическим полем: е = f(ω). Изменение диэлектрической проницаемости с изменением частоты электрического поля означает изменение электроемкости и, как следствие, изменение импеданса.
Запаздывание изменения поляризованности относительно изменения напряженности электрического поля зависит от механизма поляризации вещества. Самый быстрый механизм — электронная поляризация (см. § 12.6), так как масса электронов достаточно мала. Это соответствует частотам (около 1015 Гц), которые существенно превышают области α-, (β-, и γ-дисперсии.
Ориентационная поляризация воды, молекулы которой имеют сравнительно малую массу, соответствует γ-дисперсии (частоты около 20 ГГц).
Крупные полярные органические молекулы, например белки, имеют значительную массу и успевают реагировать на переменное электрическое поле с частотой 1—10 МГц. Это соответствует β-дисперсии.
При α-дисперсии происходит поляризация целых клеток в результате диффузии ионов, что занимает относительно большое время, и α-дисперсии соответствует область низких частот (0,1— 10 кГц). В этой области емкостное сопротивление мембран очень велико, поэтому преобладают токи, огибающие клетки и протекающие через окружающие клетки растворы электролитов.
Итак, области α-, β- и γ-дисперсии импеданса объясняются тем, что с увеличением частоты переменного электрического поля в явлении поляризации участвуют разные структуры биологических тканей: при низких частотах на изменение поля реагируют все структуры (α-дисперсия), с увеличением частоты реагируют крупные молекулы-диполи органических соединений и молекулы воды (β-дисперсия), а при самых больших частотах реагируют только молекулы воды (γ-дисперсия). Во всех случаях имеет место электронная поляризация. С увеличением частоты электрического тока (электрического поля) все меньше структур будет реагировать на изменение этого поля и меньше будет значение поляризованности Рет. Отсюда, согласно (14.48), с увеличением частоты будет уменьшаться диэлектрическая проницаемость е, а следовательно, и электроемкость С, а это, согласно (14.33), приведет к увеличению емкостного сопротивления Хс и импеданса Z. Следовательно, на фоне общего хода зависимости Z = f(ω) (см. рис. 14.10) появляются области с меньшим убыванием Z при возрастании частоты (области α-, (β- и γ-дисперсии).
Частотная зависимость импеданса позволяет оценить жизнеспособность тканей организма, что важно знать для пересадки (трансплантации) тканей и органов. Различие в частотных зависимостях импеданса получается и в случаях здоровой и больной ткани.
Импеданс тканей и органов зависит также и от их физиологического состояния. Так, при кровенаполнении сосудов импеданс изменяется в зависимости от состояния сердечно-сосудистой деятельности.
Диагностический метод, основанный на регистрации изменения импеданса тканей в процессе сердечной деятельности, называют реографией (импеданс-плетизмография).
С помощью этого метода получают реограммы головного мозга (реоэнцефалограмма), сердца (реокардиограмма), магистральных сосудов, легких, печени и конечностей. Измерения обычно проводят на частоте 30 кГц.
В заключение отметим, что знание пассивных электрических свойств биологических тканей важно при разработке теоретических основ методов электрографии органов и тканей, так как создаваемый токовыми диполями электрический ток проходит через них. Кроме того, представления о дисперсии импеданса позволяют оценить механизм действия токов и полей, используемых в терапевтических целях.
Дата добавления: 2020-11-18; просмотров: 717;











