Основные характеристики магнитного поля

Аналогично электрическому полю, необходимо для магнитного поля ввести количественную характеристику. Для этого выбирают некоторый объект — «пробное тело», реагирующее на магнитное поле. В качестве такого тела достаточно взять малую рамку (контур) с током, чтобы можно было считать, что рамка помеща­ется в некоторую точку поля. Опыт показывает, что на пробную рамку с током в магнитном поле действует момент силы М, зави­сящий от ряда факторов, в том числе и от ориентации рамки. Максимальное значение М_max зависит от магнитного поля, в котором находится контур, и от самого контура: силы тока I, проте­кающего по нему, и площади S, охватываемой контуром, т. е.

Величину

называют магнитным моментом контура с током. Таким образом,

Магнитный момент — векторная величина. Для плоского контура с током вектор р_т направлен пер­пендикулярно плоскости контура и связан с направ­лением тока I правилом правого винта (рис. 13.1).

Магнитный момент является характеристи­кой не только контура с током, но и многих эле­ментарных частиц (протоны, нейтроны, электроны и т. д.), определяя поведение их в магнитном поле.

Единицей магнитного момента служит ампер-квадратный мета (А * м²). Магнитный момент элементарных частиц, ядер, атомов и молекул выражают в особых единицах, называемых атомным ((μ_Б) или ядерным (μ_я) магнетоном Бора:

Зависимость (13.3) используют для введения силовой характе­ристики магнитного поля — вектора магнитной индукции В.

Магнитная индукция в некоторой точке поля равна отно­шению максимального вращающего момента, действующего на рамку с током в однородном магнитном поле, к магнит­ному моменту этой рамки:

Вектор В совпадает по направлению с вектором р_т в положении устойчивого равновесия контура. На рис. 13.2 показано положе­ние рамки с током в магнитном поле индукции В, соответствую­щее максимальному моменту силы (а) и нулевому (б). Последний случай соответствует устойчивому равновесию (векторы В и р_т коллинеарны).

Единицей магнитной индукции является тесла (Тл):

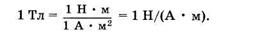
Таким образом, в поле с магнитной индукцией 1 Тл на контур, магнитный момент которого 1 А • м², действует максимальный момент силы 1 Н • м.

Магнитное поле графически изображают с помощью линий магнитной индукции, касательные к которым показывают на­правление вектора В. Густота линий, т. е. число линий, проходя­щих через единичную, перпендикулярно им расположенную площадку, пропорциональна модулю век­тора В. Линии магнитной индукции не имеют начала или конца и являются замкнутыми. Подобные поля называ­ют вихревыми. Циркуляция вектора магнитной индукции по любой ли­нии магнитной индукции не равна нулю:

Рассмотрим некоторую площадку S, находящуюся в области однородного магнитного поля индукции В (рис. 13.3). Проведем линии магнитной индукции через эту площадку. Ее проекция на плоскость, перпендикулярную линиям, равна S_o. Число линий, пронизывающих S и S_o, одинаково. Так как густота линий соот­ветствует значению В, то общее число линий, пронизывающих площадки, пропорционально

На рис. 13.3 видно, что S_o = S cos α, откуда

где В_п = В cos α — проекция вектора В на направление нормали п к площадке, Ф — магнитный поток.

В более общем случае, например, неоднородного магнитного поля поверхности, а не плоской площадки (рис. 13.4), магнитный поток Ф также пропорционален числу линий магнитной индук­ции, пронизывающих поверхность.

Единицей магнитного потока, согласно (13.6), является вебер (Вб):

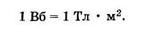
Из формулы (13.7) видно, что поток может быть как положи­тельным (cos α > 0), так и отрицательным (cos α < 0).

В соответствии с этим линии магнитной индукции, выходящие из замкнутой поверхности, считают положительными, а входя­щие - отрицательными. Так как линии магнитной индукции замкнуты, то магнитный поток сквозь замкнутую поверхность ра­вен нулю.

Как и всякая материальная субстанция, магнитное поле обла­дает энергией. Проиллюстрируем наличие такой энергии на при­мере магнитного поля, созданного контуром с постоянным током. Если разомкнуть цепь контура, то исчезнет ток и, следовательно, магнитное поле. При размыкании цепи возникнет искра или дуго­вой разряд. Это означает, что энергия магнитного поля преврати­лась в другие формы энергии — световую, звуковую и тепловую.

Выражение для объемной плотности энергии магнитного поля имеет следующий вид:

где μ — магнитная проницаемость среды, а μ₀ — магнитная посто­янная.

Закон Ампера

Одним из главных проявлений магнитного поля является его силовое действие на движущиеся электрические заряды и токи. В результате обобщения многочисленных опытных данных А. М. Ампером был установлен закон, определяющий это силовое воздействие.

Приведем его в дифференциальной форме, что позволит вычис­лять силу, действующую на различные контуры с током, располо­женные в магнитном поле.

В проводнике, находящемся в магнитном поле, выделим доста­точно малый участок dl, который можно рассматривать как век­тор, направленный по току (рис. 13.5). Произведение Idl называ­ют элементом тока. Сила, действующая со стороны магнитного поля на элемент тока,

где k — коэффициент пропорциональности; в СИ k = 1, поэтому

или в векторной форме

Для плоского контура с током находим силу, действующую на участок I проводника со стороны магнитного поля, интегрированием скалярного выражения (13.10):

Соотношения (13.9)—(13.12) выражают закон Ампера.

Рассмотрим некоторые примеры на применение формулы (13.11).

1. Прямолинейный участок проводника с током I длиной l, расположенный в однородном магнитном поле под углом (3 к маг­нитной индукции В (рис. 13.6). Для нахождения силы, действую­щей на эту часть проводника со стороны магнитного поля, интег­рируем (13.12) и получаем

2. Прямоугольная рамка KLMN с током I, помещенная в одно­родное магнитное поле индукции В (рис. 13.7, а). Пронумеруем стороны рамки и обозначим силы, действующие на них со сторо­ны магнитного поля, F_1, F₂, F₃, F₄.

Силы F₁ и F₃, приложенные к серединам соответствующих сторон,направлены противоположно вдоль оси и по формуле (13.13) Лоренца не изменяет равны. Силы же F₂ = F₄ = IBb создают пару сил, момент которой (рис. 13.7, б)

Так как Iba = IS =p_m, то из (13.14) имеем

или в векторной форме

Фактически на основе этой зависимости в § 13.1 было введено понятие вектора магнитной индукции.