Энергия электрического поля

Система зарядов или заряженных тел, заряженный конденса­тор обладают энергией.

В этом можно убедиться, разряжая, например, конденсатор че­рез лампочку, присоединенную к нему: лампочка вспыхнет.

Вычислим энергию поля конденсатора. Чтобы зарядить его, будем многократно переносить положительный заряд dq с одной обкладки на другую. По мере его переноса увеличивается напря­жение между обкладками конденсатора. Работа, которую необхо­димо совершить против сил электрического поля для зарядки конденсатора, равна энергии конденсатора:

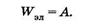
Элементарная работа по перемещению заряда против сил поля равна dA = Udq. Перенос заряда dq с одной обкладки конденсатора на другую изменяет напряжение его на dU, и тогда из формулы для электроемкости запишем dq = CdU, а значит, dA = CUdU.

роинтегрировав это равенство в пределах от U_o = 0 до некото­рого конечного значения U, найдем выражение для энергии поля заряженного конденсатора:

или, учитывая, что С = q/U,

Если, не изменяя заряда на обкладках кон­денсатора, отключенного от источника на­пряжения, раздвинуть его пластины от рас­стояния 1_г до 1₂, то электроемкость умень­шится (см. 12.34). Как видно из (12.44), при этом энергия конденсатора с увеличе­нием объема, занимаемого электрическим полем (рис. 12.27), возрастет, а напряженность поля останется постоянной. Отсюда ясно, что энергия заря­женного конденсатора сосредоточена в объеме, занимаемом элект­рическим полем.

Более убедительно пояснить существование энергии электри­ческого поля можно на примере переменного электромагнитного поля (передача сигнала на расстояние, давление света и т. п.).

Выразим энергию поля через его характеристики. С этой целью преобразуем (12.43), подставив выражение для емкости плоского конденсатора (12.34) и напряжение из (12.14):

где V = Sl — объем, занимаемый электрическим полем конденса­тора.

Предполагая, что электрическое поле плоского конденсатора однородно, разделим (12.45) на объем и получим объемную плотность энергии поля:

Единицей объемной плотности является джоуль на кубический метр (Дж/м³).

В заключение заметим, что формула (12.46) справедлива и для неоднородного электрического поля, но тогда она выражает объ­емную плотность энергии в точке. Энергия неоднородного поля может быть найдена интегрированием (12.46) по соответствующе­му объему

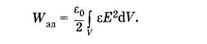
В общем случае диэлектрическая проницаемость различна в разных точках среды, т. е. зависит от координат, поэтому в этой формуле 8 входит под знак интеграла.