Модель единичного индекса (модель У. Шарпа)

В 1963 г. американский экономист У. Шарп (William Sharpe) предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений. В дальнейшем этот метод модифицировался и в настоящее время известен как одноиндексная модель Шарпа (Sharpe single-index model).

В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две случайные переменные величины – независимую Х и зависимую Y линейным выражением типа Y = α + βЧХ. В модели Шарпа независимой считается величина какого-то рыночного индекса. Таковыми могут быть, например, темпы роста валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т. п. Шарп в качестве независимой переменной рассматривал доходность r_m, вычисленную на основе индекса Standart and Poor’s (S&P500). В качестве зависимой переменной берется доходность r_i какой-то i-ой ценной бумаги. Поскольку зачастую индекс S&P500 рассматривается как индекс, характеризующий рынок ценных бумаг в целом, то обычно модель Шарпа называют рыночной моделью (Market Model), а доходность r_m – доходностью рыночногопортфеля.

Модель Шарпа рассматривает взаимосвязь доходности каждой ценной бумаги с доходностью рынка в целом. Основные допущения модели Шарпа:

– в качестве доходности ценной бумаги принимается математическое ожидание доходности;

– существует некая безрисковая ставка доходности R_f, т. е. доходность некой ценной бумаги, риск которой всегда минимален по сравнению с другими ценными бумагами;

– взаимосвязь отклонений доходности ценной бумаги от безрисковой ставки доходности (далее: отклонение доходности ценной бумаги) с отклонениями доходности рынка в целом от безрисковой ставки доходности (далее: отклонение доходности рынка) описывается функцией линейной регрессии;

– под риском ценной бумаги понимается степень зависимости изменений доходности ценной бумаги от изменений доходности рынка в целом;

– считается, что данные прошлых периодов, используемые при расчете доходности и риска, отражают в полной мере будущиезначения доходности.

По модели Шарпа отклонения доходности ценной бумаги связываются с отклонениями доходности рынка функцией линейной регрессии вида:

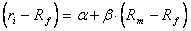, (4.1)

где (r_i – R_f) - отклонение доходности ценной бумаги от безрисковой; (R_m – R_f) - отклонение доходности рынка от безрисковой; α, β - коэффициенты регрессии.

Исходя из этой формулы, можно по прогнозируемой доходности рынка ценных бумаг в целом рассчитать доходность любой ценной бумаги, его составляющей:

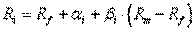, (4.2)

где α_i , β_i - коэффициенты регрессии, характеризующие данную ценную бумагу.

Теоретически, если рынок ценных бумаг находится в равновесии, то коэффициент α_i будет равен нулю. Но так как на практике рынок всегда разбалансирован, то α_i показывает избыточную доходность данной ценной бумаги (положительную или отрицательную), т. е. насколько данная ценная бумага переоценивается или недооценивается инвесторами.

Коэффициент β называют β -риском, так как он характеризует степень зависимости отклонений доходности ценной бумаги от отклонений доходности рынка в целом. Основное преимущество модели Шарпа - математически обоснована взаимозависимость доходности и риска: чем больше β - риск, тем выше доходность ценной бумаги. В соответствии с моделью Шарпа доходность портфеля ценных бумаг – это среднее взвешенное значение показателей доходности ценных бумаг, его составляющих, с учетом β - риска. Доходность портфеля определяется по формуле:

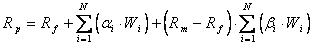, (4.3)

где R_f- безрисковая доходность;

R_m- ожидаемая доходность рынка в целом;

Риск портфеля ценных бумаг может быть найден с помощью оценки среднего квадратичного отклонения функции R_f и определяется по формуле:

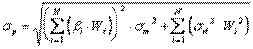, (4.4)

где σ_m - среднее квадратическое отклонение доходности рынка в целом, т. е. показатель риска рынка в целом;

β_i , σ_ri , β - риск и остаточный риск i - ой ценной бумаги;

С использованием модели Шарпа для расчета характеристик портфеля прямая задача приобретает вид:

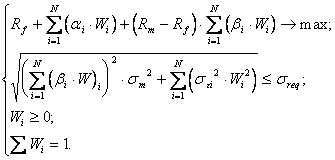
Основной недостаток модели — необходимость прогнозировать доходность фондового рынка и безрисковую ставку доходности. Модель не учитывает колебаний безрисковой доходности. Кроме того, при значительном изменении соотношения между безрисковой доходностью и доходностью фондового рынка модель дает искажения.

Таким образом, модель Шарпа применима при рассмотрении большого количества ценных бумаг, описывающих большую часть относительно стабильного фондового рынка.

Вопросы для самоконтроля

1. Дайте определение и назовите основные виды ценных бумаг.

2. Какие виды акций вы знаете? Дайте определение пакета акций. Каковы имущественные и неимущественные права акций?

3. В чем сущность облигации? Назовите виды облигаций. Что значит «обеспечение облигаций»?

4. Дайте определение векселю. Какие вы знаете виды и формы векселей? Что означают «переводной вексель», «простой вексель»?

5. Какие вы знаете производные инструменты (деривативы)? Перечислите основные виды деривативов.

6. Как рассчитываются цена и доходность ценных бумаг?

7. Как осуществляется механизм формирования и управления портфелем ценных бумаг?

8. Какие риски инвестирования в ценные бумаги вы знаете?

9. Какие существуют методы оценки доходности финансовых активов?