Методы обработки экспертной информации
После проведения опроса экспертов осуществляется обработкарезультатов. Исходной информацией для нее являются заполненные экспертами анкеты, которые подвергаются логической проверке, сводке и подсчету полученных ответов и оценок, а также анализу содержательных обоснований мнений экспертов. Целью обработки является получение обобщенных данных и новой информации, содержащейся в скрытой форме в экспертных оценках. На основе результатов обработки экспертизы формируется решение проблемы.
В зависимости от характера задач, решаемых в процессе экспертизы, могут быть использованы следующие методы измерения (и получены соответствующие оценки):
-непосредственная оценка;
-ранжирование;
-парное сравнение;
-множественные сравнения;
-последовательное сравнение и другие.
Непосредственная оценка – процедура присвоения альтернативам числовых значений в заданной шкале. Мнение эксперта по поводу каждого оцениваемого варианта определяется точкой на отрезке числовой оси. Чаще всего при этом используются балльные шкалы, поэтому другое название данной формы экспертного опроса – метод балльных оценок.
Ранжирование – процедура упорядочения альтернативных вариантов, выполняемая экспертом, в результате которой получается последовательность предпочтений. Числовым выражением мнения эксперта является рангальтернативы в данной последовательности. Достоинство ранжирования – простота реализации процедур. Недостатком является практическая невозможность упорядочения большого числа объектов.
Парное сравнение – процедура установления предпочтения альтернатив при сравнении всех возможных пар. Мнение эксперта обычно представляется в виде заполнения матрицы предпочтений (квадратная матрица, размерность которой определяется количеством оцениваемых альтернативных вариантов). При сравнении пары объектов возможно либо отношение строгого порядка, либо отношение эквивалентности. Таким образом, парное сравнение так же, как и ранжирование, есть измерение в порядковой шкале.
Пример. Матрица парных сравнений и расчет на ее основе их весовых значений и рангов представлены в табл. 5.2.
Элементы матрицы парных сравнений [aie] определяются следующим образом:
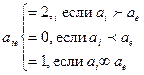
Для рассматриваемого примера матрица парных сравнений  имеет следующий вид (табл. 5.2.графы 2-7).
имеет следующий вид (табл. 5.2.графы 2-7).
Таблица.5.2
 e
i e
i
|  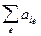
| Вес Пi | Итоговый порядок | ||||||
| 0,26 | |||||||||
| 0,31 | |||||||||
| 0,06 | |||||||||
| 0,06 | |||||||||
| 0,20 | |||||||||
| 0,11 | |||||||||
| И | т | о | г | о | 1,00 |
Во многих случаях использование парных экспертных сравнений дает более надежные результаты, чем обычное ранжирование.
Множественные сравнения отличаются от парных тем, что экспертам последовательно предъявляются не пары, а тройки, четверки и т.д. альтернатив. Эксперт упорядочивает их по важности или разбивает на классы в зависимости от целей экспертизы. Множественные сравнения занимают промежуточное положение между парным сравнением и ранжированием. Они позволяют рассматривать одновременно большее, чем при парном сравнении, количество объектов. В то же время, при большом количестве сравниваемых объектов работа эксперта может быть затруднена, что скажется на ее результатах.
Последовательное сравнение – комплексная процедура экспертного опроса, включающая ранжирование и непосредственную оценку альтернативных вариантов. Один из самых эффективных экспертных методов.
Соответственно с формой опроса и типом полученных экспертных оценок производится их анализ и согласование. Групповое решение принимается на основе индивидуальных мнений экспертов на базе использования, прежде всего, следующих методов:
- получение среднеарифметического илисредневзвешенногозначенияиндивидуальных оценок. Это наиболее простой способ получения групповых оценок, однако, он не гарантирует согласованности полученной оценки;
- правило “большинства”, базирующееся на общих условиях превращения совокупности индивидуальных оценок в согласованное групповое мнение;
- в качестве групповой оценки может приниматься среднее суждение экспертов (медиана) (например, в методе Дельфи);
- средний ранг полученных индивидуальных порядков и другие методы.
При анализе результатов экспертизы оценивается степень согласованности мнений экспертов и, если возможно, выделяются группы экспертов с “близкими” мнениями. Также оценивается “разброс” мнений, анализируется влияние характеристик экспертов на содержание их ответов. Внутри однородных групп выявляются “объединенные” ответы, на базе которых формируются результаты коллективной экспертизы.
Характеристики согласованности полученных групповых оценок зависят от применяемых типов шкал. Так, для среднеарифметической групповой оценки используется коэффициент вариации.При этомна практике часто применяется эмпирическое правило – групповая оценка признается согласованной, если коэффициент вариации меньше 33 %. Для ранговой шкалы используется коэффициент конкордации. Согласованность оценок для номинальной шкалы может быть оценена с использованием коэффициента ассоциации. Коэффициент ассоциации учитывает число совпадающих и несовпадающих ответов (но не учитывает их последовательности).
Пример. Для разработки стратегии необходимо оценить предполагаемый спрос на продукцию фирмы. Используется экспертный опрос. В опросе приняли участие 43 эксперта.
Получен следующий результат (среднеарифметическое значение индивидуальных экспертных оценок):
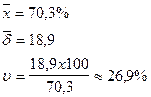
Так как коэффициент вариации 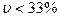 , то полученная оценка считается согласованной. Далее необходимо рассчитывать величину интервала, которому принадлежит полученная оценка, т.е.
, то полученная оценка считается согласованной. Далее необходимо рассчитывать величину интервала, которому принадлежит полученная оценка, т.е. 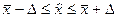 , где
, где 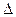 - предельная ошибка средней;
- предельная ошибка средней;
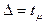 , где t - коэффициент доверия (t - критерий Стъюдента).
, где t - коэффициент доверия (t - критерий Стъюдента).
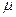 - среднеквадратическая ошибка среднеарифметической.
- среднеквадратическая ошибка среднеарифметической.
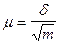
где m - количество экспертов.
Для нашего примера: 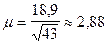 ,
,
при p =0,95, t = 2,0, следовательно 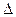 = 2 х 2,88 = 5,76
= 2 х 2,88 = 5,76
70,3 - 5,76 < 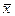 < 73,3 + 5,76
< 73,3 + 5,76
или
64,5 % < x < 76,06%
Таким образом, по мнению экспертов, предполагаемый спрос ожидается в указанном интервале.
Существуют специально разработанные методы формирования группового ответа, с помощью которых можно уменьшить разброс индивидуальных мнений и получить согласованную групповую оценку (например, метод Дельфи; методы, основанные на отборе экспертной группы с высоким коэффициентом согласованности мнений). Для повышения объективности экспертных методов исследования систем управления следует учитывать не только групповые мнения экспертов, но и противоречивые, «редкие» мнения.
Существование сложных систем и процессов привело к необходимости формированию процедур сложных экспертиз, повышающих объективность получения оценок путем расчленения большой исходной неопределенности проблемы (системы) исследования, предлагаемой эксперту для изучения, в процессе декомпозиции на более мелкие, лучше поддающиеся осмыслению. Подобные экспертизы описаны, например, в [10, 35].
Существуют определенные ошибки, которые необходимо учитыватьв практике экспертного оценивания:
· преувеличение возможностей экспертных оценок;
· преуменьшение возможностей экспертных оценок;
· использование некомпетентных экспертов;
· недостаточная информированность экспертов об объекте экспертизы;
· нечеткая постановка задач перед экспертом;
· излишнее увлечение количественными оценками;
· нарушение принципов теории измерений;
· неоправданное увлечение «свертками»;
· конформизм экспертов;
· конъюнктурность оценок;
· неправильная обработка результатов экспертизы и некорректная интерпретация результатов и другие.
5.4. Системное моделирование
Постоянное усложнение систем, с одной стороны, а также развитие науки и вычислительных возможностей – с другой, приводят к появлению все большего количества «комбинированных» методов исследований, в которых используются и сложные формальные модели, и экспертные оценки, и компьютерные эксперименты.
Основным требованием к любой модели является ее адекватность моделируемому объекту. В настоящее время меняется подход к моделированию систем. В период становления моделирование систем осуществлялось следующим образом: выбирался некоторый наиболее подходящий, как правило, математический метод, который модифицировался и дорабатывался с учетом особенностей системы – оригинала и доводился до вычислительных процедур. В настоящее время принята иная концепция моделирования систем, получившая название «гoмеостатической». На практике она реализуется различными способами, но суть у них одна: пошаговое приведение исходной модели к состоянию, подобному объекту-оригиналу, за счет включения в модель программных механизмов адаптации и интерпретации, а также оргaнизации режима эффективного диалогa с исследователем [24, С.168].
Идея построения гомеостатической модели проста, но ее практическое воплощение требует привлечения принципиально новых информационных технологий. На первом шаге, используя данные описательной модели, строится основа системной модели (ее исходное приближение), учитывающая априорно известные свойства и аспекты моделируемой системы. Этот «каркас» еще далек с точки зрения адекватности объекту-оригиналу и не позволяет сформулировать сколько-нибудь значимые практические выводы, но одновременно в него закладываются специальные aлгоритмы, позволяющие изменять исходные предпосылки (базовые аксиомы и правила вывода) по мере получения новых данных об объекте изучения. Далее проводится модельный эксперимент. Полученные при этом данные используются для корректировки каркаса - формируется модель системы в первом ее приближении. Затем уже с помощью этой модели проводится эксперимент, по результатам которого она вновь корректируется - формируется модель системы во втором ее приближении, и так далее. Такой циклический обучающий процесс «эксперимент - данные - корректировка» многократно повторяется и никогда не завершается построением окончательной системной модели. Bceгдa это будет некое приближение к системе-оригиналу, нуждающееся в уточнении в ходе дальнейших исследований.
По замыслу создания системные гомеостатические модели - это открытые человекомашинные системы, в которых компьютер выступает как интеллектуальный партнер системного аналитика, ведущий с ним диалог в реальном масштабе вpeмени. Для ведения эффективного диалога необходимо выполнение следующих условий:
· прогpаммный комплекс системной модели должен обеспечивать накопление, формирование, хранение и обработку данных и знаний об изучаемой проблемной области (модель должна «понимать», о чем идет речь в данных исследованиях и экспериментах);
· должна быть обеспечена языковая совместимость прогpаммного комплекса системной модели с человеком-исследователем (модель должна адекватно «воспринимать» информацию, сообщаемую исследователем, а исследователь должен понимать информацию, выдаваемую моделью);
· по указанию исследователя модель должна уметь планировать и производить необходимые вычисления, осуществлять логическую обработку сообщаемых ей фактов, а также данных, получаемых в peзультате вычислений и логических выводов. Принципиальная особенность гомеостатических системных моделей состоит в необходимости их обучения.
Общая схема исследований с помощью системной гoмеостатической модели включает следующие этапы [24, С. 183].
1. Выделение и уяснение проблемы.
2. Концептуализация проблемы: суммирование известных сведений, вербальное описание модели, выбор объекта исследования и критериев принятия решений.
3. «Идеализация» проблемы – декомпозиция объекта исследования, формулирование частных задач исследования и базовых аксиом.
4. Идентификация модели – определение входных переменных, констант, критериев и показателей эффективности.
5. Реализация модели – структурный и параметрический синтез, разработка алгоритмов и программ, их комплексирование и отладка.
6. Проверка модели – сопоставление результатов моделирования с наблюдениями и экспериментами, оценка адекватности, чувствительности, точности, экономичности и работоспособности модели.
7. Обучение и исследование модели – ввод новых аксиом и правил вывода, проведение модельных экспериментов.
8. Интерпретация модельных исследований – композиция, обобщение и содержательная трактовка результатов моделирования.
9. Оформление результатов исследования.
Следует отметить: во-первых, подобные системные исследования итеративны; во-вторых, они предполaгают обязательную интеграцию теоретических модельных экспериментов с наблюдениями, эмпирическими исследованиями, натурными (лабораторными) экспериментами; в-третьих, системная модель - это некоторая концептyальная (символьная) система, органически вписанная в общий процесс проведения системного исследования и не существующая вне его.
Системные модели не следует рассматривать как противопоставление традиционному математическому моделированию. Здесь «стирается гpaнь между стремлением к тотальной формализации и логико-интyитивным (эвристическим) подходом к анализу системных явлений». Важнейшим отличием системного моделирования от традиционного математическогo является использование языков представления знаний, позволяющих отражать различные аспекты проблемной области, наблюдаемые факты и закономерности, описывать эти знания не только на количественном, но и на качественном уровне. По сути, системное моделирование - это процесс восприятия, фиксации, переработки и получения новых знаний на базе использования информационных компьютерных технологий. Поэтому проблема представления знаний находится в центре внимания специалистов по системному моделированию. В этой проблеме кардинальным является вопрос о структуре языка представления знаний. Частично ответить на этот вопрос удaется при изучении способов построения логико-лингвистических системных моделей и процедур «мягкиx» вычислений.
Эти понятия вошли в обиход специалистов по системному анализу и дрyгиx отраслей знания в конце ХХ века как оргaническое объединение теоретических результатов трех научных направлений: искусственногo интеллекта, математической лингвистики и компьютерных языковых технологий. Их появление связано с тем, что в сферу интересов ученых все чаще стали попадать объекты, для познания которых либо невозможно построить достаточно адекватную математическую модель, либо модель столь сложна, что с ее помощью не удается выяснить причинные связи между изучаемыми процессами и объяснить те или иные результаты. К числу таких объектов относятся системы самой различной природы, для которых помимо всех остальных черт больших (сложных) систем характерны следующие свойства:
· большое количество слабо формализуемых и зачастую противоречивых целей функционирования с одновременной их изменчивостью (ситуативностью) во времени;
· конфликтный и многоаспектный характер взаимоотношений как между их компонентами, так и со средой при сильном влиянии человеческого фактора;
· преимущественно понятийный характер исходных описаний, условий функционирования и внешних огpаничений.
Если сравнивать естественные и математические языки по двум условным характеристикам: семaнтической силе СС = {0 ... 1}, отражающей возможности данногo языка по многoаспектному описанию ситуаций реальногo мира, и мощности инструментальных средств МИС = {0 ... 1}, oтpaжающей способность языка производить формально-эквивалентные преобразования своих конструкций, то оказывается, что чем выше семaнтическая сила языка, тем ниже мощность eгo инструментальных средств, и наоборот чем выше мощность языковых инструментальных средств, тем ниже семантическая сила языка. В первом случае приоритет принадлежит естественным языкам, во втором – математическим. Наличие противоположных тенденций свидетельствует о существовании некоего компромисса, то есть таких искусственных языковых средств, которые, с одной стороны, позволяют достаточно адекватно описывать проблемные ситуации в их многoобразии а, с дрyгой, - обладают достаточно развитым инструментaрием для производства формальных эквивалентных преобразований. К таким языковым средствам относятся: нечеткие множества, реляционные и ролевые языки, составляющие в совокупности лингвистическую основу «мягких» вычислений. Более подробные сведения об этих языках можно получить в специальной литературе[36].
Языковые средства «мягкиx» вычислений следует рассматривать в качестве дальнейшего развития и наращивания возможностей традиционных математических языков. Они предоставляют достаточно мощный инструментарий для формализованного описания реальных ситyаций, и одновременно указывают направление для внедрения в практику научных исследований современных компьютерных технологий. Более тoгo, они сами оказывают позитивное влияние на развитие этих тexнoлогий, например, в части создания баз знаний, поиска решений, aвтомaтизации управленческой деятельности в слабо формализуемых проблемных областях.
Традиционный подход к формализации задач оценки и поиска peшений состоит в определении существенных характеристик проблемной ситyации, которые совместно с существующими между ними отношениями могут быть описаны количественно. В логико-лингвистических моделях использование этих методов неприемлемо по следующим причинам. Во-первых, в этих моделях переменные не количественные, а лингвистические, то есть их значениями выступают не числа, а слова и предложения ecтeственного или искусственного языка. Во-вторых, связи между переменными выражаются не в виде математических уравнений, а задаются с помощью лингвистических, логических или словесных выражений. В-третьих, критерии выбора формулируются не в виде точного математического функционала, а описываются качественными формулировками, например, в виде текстовых указаний по предпочтительности, недопустимости или желательности того или иного варианта решения.
Поэтому в логико-лингвистических моделях реализуются специфические методы оценки и поиска решений, ориентированные на качественное (понятийное) описание компонентов решений, связей между ними и критериев выбора. В этой особенности скрыто и ограничение применимости данных моделей. Поэтому с практической точки зрения наилучшим следует признать комплексный подход к моделированию систем, при котором логико-лингвистические модели и мягкие вычислительные процедуры используются как инструмент структурирования проблемы и выявления ее наиболее существенных аспектов. Тем самым обеспечивается корректный переход к созданию имитационных математических моделей и применению количественных математических методов оптимизации, позволяющих не только осмыслить, но доказать и более убедительно подтвердить рациональность выбора.
Существует значительное количество направлений развития представленного подхода. Особое значение имеет применение этих моделей в исследовании процессов управления. Рассмотрим наиболее развитые из этих направлений.
Алгоритмы интеллектуального автоматического управления
Классическая процедура синтеза управляющего автоматического устройства обычно включает в себя следующие этапы:
а) построение или получение математической модели объекта управления;
б) задание требований к качеству процессов управления, т.е. к поведению системы автоматического управления в целом;
в) определение структуры и параметров управляющего устройства (также в виде некоторой аналитической зависимости, связывающей различные векторы).
Применение данного подхода на практике встречается с рядом серьезных затруднений. Так, точная математическая модель реального объекта часто оказывается слишком сложной или совсем неизвестной. Изменения окружающей среды приводят к действию на объект различного рода возмущений - сигнальных, параметрических и структурных, представляющих собой дополнительный источник неопределенности о характеристиках объекта. Сложность решения данной задачи обусловлена и тем, что сами требования к системе зачастую могут быть заданы лишь приближенно. Более того, некоторые из них вообще могут оказаться взаимно противоречивыми. Поэтому понятно, что стремление найти решение задачи синтеза в классе стандартных алгоритмов управления оказывается выполнимым только в тех случаях, когда объект описывается достаточно простой и понятной моделью, т.е. справедлива схема "простой объект " - "простой регулятор".
Попытка построения адаптивных регуляторов, параметры которых автоматически перестраиваются при изменении параметров объекта, такжеимеет весьма ограниченную область применения. Причины здесь примерно те же: трудно подобрать простой и надежный алгоритм адаптации, работоспособный в случае широкого диапазона изменения параметров объекта. Если объект управления относится к категории сложных динамических объектов, то выбор алгоритма адаптации резко усложняется, поскольку возникает проблема сходимости (устойчивости) процессов адаптации в системе; трудно подобрать оптимальные значения параметров устройства адаптации; многие из существующих методик анализа и синтеза адаптивных систем связаны с чрезмерным упрощением задачи.
Выход из сложившейся ситуации был найден в использовании алгоритмов интеллектуального управления (англ. - intelligent control), предполагающих отказ от необходимости получения точной математической модели объекта, ориентации на применение «жестких» (как правило, линейных) алгоритмов формирования управляющих воздействий, стремления, во что бы то ни стало, воспользоваться известными разработчику методиками синтеза, ранее положительно зарекомендовавшими себя для других, более простых классов объектов.
В основе интеллектуального управления лежит идея построения высокоорганизованных систем автоматического управления, основанных на использовании моделей переменной сложности и неопределенности, с выполнением таких интеллектуальных функций, традиционно присущих человеку, как принятие решений, планирование поведения, обучение и самообучение в условиях изменяющейся внешней среды. Подобучением понимается способность системы улучшать свое поведение в будущем, основываясь на экспериментальной информации, которую она получала в прошлом, о результатах взаимодействия с окружающей средой.Самообучение - это обучение без внешней корректировки, т.е. без указаний "учителя".
Интеллектуальной системой управления считается такая, в которой знания о неизвестных характеристиках объекта управления и окружающей среды формируются в процессе обучения и адаптации, а полученная при этом информация используется в процессе автоматического принятия решений так, что качество управления улучшается. Необходимым признаком интеллектуальной системы является наличие базы знаний, содержащей сведения (факты), модели и правила, позволяющие уточнить поставленную задачу управления и выбрать рациональный способ ее решения. Нередко об интеллектуальных системах говорят как осистемах, основанных на знаниях(knowledge - based systems).
Наибольшее распространение при исследовании и проектировании интеллектуальных систем управления получили методы, относящиеся к следующим четырем классам:
• экспертные системы;
• нечеткие регуляторы;
• нейронные сети;
• генетические алгоритмы.
Экспертные системы (expert systems) имеют дело с задачами искусственного интеллекта, работая с символической информацией для получения выводов об окружающей среде и формирования управленческих решений с учетом характера сложившейся (или прогнозируемой) ситуации. Экспертные системы накапливают эвристические знания и манипулируют ими, пытаясь имитировать поведение эксперта. Основные компоненты такой системы осуществляют следующие функции.
База данных содержит непрерывно обновляемые данные (предыдущие, текущие, прогнозные) о характеристиках объекта и внешней среды, а также информацию о граничных (критических, предельно допустимых) значениях соответствующих параметров. База знаний содержит знания о специфике работы конкретного объекта, целях, стратегии и алгоритмах управления, о результатах идентификации и прогноза его характеристик. Подсистема логического вывода осуществляет выбор рациональной (наиболее подходящей в данной ситуации) структуры и параметров регулятора, а также, возможно, алгоритмов идентификации и прогноза. Подсистема интерфейса предназначена для организации интерактивного режима по наполнению базы знаний с участием эксперта (режим обучения) и обеспечения общения с пользователем - оператором, включая объяснение механизма принятия тех или иных решений по управлению (режим эксплуатации).
Данная система обеспечивает выполнение таких важных функций, как:
• построение динамической модели объекта и его среды;
• поддержание контакта с внешниммиром (датчиками, СУБД, регулятором).
Данное обстоятельство позволяет относить рассматриваемую экспертную систему к классудинамических ("активных") экспертных систем, или экспертных системреального времени.
Математический аппарат теории экспертных систем базируется на использовании логических моделей, семантических сетей, правил типа "ЕСЛИ ....ТО".
Нечеткие регуляторы (“fuzzy controllers”). Идеи нечеткой логики, впервые высказанные в 1964 г. Л. Заде, свое первое применение в задачах управления реальными, прежде всего, техническими объектами нашли в Европе. В последующем, данный подход, в силу своей наглядности и универсальности, получил применение и значительное распространение во многих странах и областях деятельности.
Классическая теория множеств построена на дихотомии, то есть элемент х может либо принадлежать множеству А, либо не принадлежать ему. В теории нечетких множеств дихотомия отсутствует. Вместо нее принадлежность элемента х множеству А задается функцией принадлежности. Функция принадлежности может выражаться как числами из интервала [0, 1], так и в виде лингвистических переменных, то есть переменных, значениями которых выступают не числа, а слова и словосочетания. Содержательная трактовка функции принадлежности зависит от задачи, в которой используется нечеткое множество. Возможные тpaктовки функции принадлежности: степень соответствия понятию А; вероятность; возможность; полезность; истинность; правдоподобность; значение функции. Таким образом, нечеткие множества представляют собой расширение обычных (строгиx) множеств.
Главное достоинство нечетких регуляторов - возможность эффективного управления сложными динамическими объектами в условиях неопределенности их характеристик путем моделирования механизма обработки знаний по аналогии с поведением высококвалифицированного оператора (эксперта). Эти методы получают все большее распространение в практике исследования и управления сложными системами – в управлении финансами, маркетингом, инвестиционными проектами и др.
Нейронные сети. История искусственных нейронных сетей (artificial neural networks) начинается с работ американских ученых У. Мак-Каллока, В. Питса (1943 г. - модель формального нейрона) и Ф. Розенблата (1958 г. - однослойная нейронная сеть, названная им персептроном). В настоящее время поднейронными сетями понимаются параллельные вычислительные структуры, которые моделируют процессы, обычно ассоциируемые с процессами человеческого мозга. Нейросетевым моделированием называется способ имитации процессов функционирования реальных систем на основе искусственных нейронных сетей, которые представляют собой устройства, использующие огромное число взаимосвязанных элементарных условных рефлексов, названных по имени канадского физиолога Д. Хебба «синапсами Хебба».
Нейронные сети обладают способностью приобретения знаний о предметной области, обучаясь на примерах и подстраивая свои веса для интерпретации предъявляемых им многоразмерных данных. В настоящее время этот аппарат все шире применяется для анализа сложных, в том числе социально-экономических систем, например, товарных и финансовых рынков. Нейронные сети используются для задач идентификации и классификации, управления, адаптации характеристик системы к параметрическим возмущениям.
Генетические алгоритмы (genetic algorithms) - это большая группа методов адаптивного поиска и многопараметрической оптимизации, интенсивно развивающихся в последние годы, как для их самостоятельного применения, так и в сочетании с другими методами интеллектуального управления. Их происхождение связано с использованием принципов естественного отбора и генетики. Традиционные методы поиска обычно предполагают дифференцируемость исследуемой целевой функции от ее параметров и, как правило, используют градиентные процедуры. Генетические алгоритмы отличаются от обычных методов оптимизации. По своей сути, они представляют собой метод параллельного поиска глобального экстремума, основанный на использовании в процессе поиска сразу нескольких, закодированных соответствующим образом точек (кандидатов на решения), которые образуют развивающуюся по определенным случайным законам «популяцию». Используемые при этом механизмы отбора, впервые четко сформулированные еще Ч. Дарвиным ("выживает наиболее приспособленный"), позволяют отсеять наименее подходящие варианты и, наоборот, выделить, а затем и усилить положительные качества тех вариантов, которые наиболее полно отвечают поставленной цели.
Выводы
Системный анализ базируется на разработке процедур, которые включают методы различных классов, в том числе, формализованных и экспертных. Знание этих методов и умение их комбинировать является залогом успеха в исследовании сложных объектов и проблем.
Основой системных исследований являются модели, представляющие собой упрощенные отображения сложных объектов. Модели бывают самых разных типов, но все они должны удовлетворять ряду требований, важнейшим из которых является адекватность.
Системный анализ оперирует практически всеми формальными методами и средствами, пригодными для моделирования. В зависимости от специфики математического аппарата эти методы разделяют на классы аналитических, статистических, логических и информационных. Каждый из них используют для изучения различных типов систем и проблем.
В системном анализе формальные методы, как правило, не являются основным инструментом исследования, особенно на начальных этапах. Формальные методы позволяют исследовать проблемы, которые относятся к типу хорошо структуризованных. В то же время, объектом системного анализа являются, как известно, слабоструктуризованные проблемы. Важная роль в их изучении принадлежит экспертам. Несмотря на субъективизм оценок, эксперты являются эффективным «инструментом» исследования сложных систем, особенно в сочетании с другими методами.
В последние годы достижения в области вычислительных процедур и компьютерных систем привели к появлению принципиально новых возможностей системного моделирования и построению адаптивных системных человеко-машинных моделей. Они позволяют расширить возможности традиционного математического моделирования, включая в рассмотрение качественные характеристики проблемы. Эти модели позволяют повысить адекватность описания проблем и обоснованность выбора рациональных решений.
Вопросы и задания для самоконтроля
1. Для каких классов проблем целесообразно использовать формализованные методы исследований?
2. Какое явление лежит в основе построения любой модели?
3. Каковы основные требования к моделям?
4. Что представляет собой концептуальная модель?
5. Приведите признаки классификации моделей.
6. Какими бывают основные типы моделей систем?
7. Каковы особенности применения аналитических методов в исследовании систем?
8. В чем преимущества и недостатки методов математического программирования?
9. Для каких проблем можно использовать статистические методы исследования?
10. Каковы возможности имитационных методов моделирования?
11. При каких условиях следует использовать логические методы?
12. Каковы основные направления информационных методов?
13. В чем состоит ограниченность формализованных методов в исследовании систем?
14. В чем сущность экспертных методов?
15. При каких условиях используются экспертные оценки?
16. Каковы основные процедуры коллективных экспертных оценок?
17. Как можно уменьшить субъективизм экспертных оценок?
18. В чем состоит специфика эвристического программирования?
19. Каковы основные этапы проведения экспертизы?
20. В чем состоят основные задачи и методы анализа экспертной информации?
21. Как определяется согласованность экспертных оценок?
22. В чем суть «гомеостатической» концепции системного моделирования?
23. Что такое «мягкие» вычисления?
24. Каковы возможности логико-лингвистического моделирования систем?
25. Каковы основные направления развития современного системного моделирования?
Дата добавления: 2020-11-18; просмотров: 1028;











