Параллактический треугольник светила

Меридиан наблюдателя, меридиан и вертикал светила являются дугами больших кругов. Пересекаясь, они образуют на поверхности небесной сферы сферический треугольник, называемый параллактическим или полярным треугольником светила (за рубежом – навигационным или позиционным)

(рис. 3.4.). Вершинами параллактического треугольника являются повышенный полюс P_N или P_S, зенит Z и место светила С.

Элементы треугольника, т.е. его стороны и углы, представляют собой сферические (горизонтные или экваториальные) координаты светила и географические координаты наблюдателя. Угол при повышенном полюсе ZP_NC равен практическому часовому углу светила t_пр, угол при зените CZP_N - азимуту светила А. Сторонами треугольника являются: дуга меридиана наблюдателя ÈP_NZ = 90° - j, дуга меридиана светила ÈP_NС = 90° - d и дуга вертикала светила ÈZC = 90° - h.

Угол q при светиле носит название параллактического угла.

Географическая долгота наблюдателя l входит в скрытом виде в часовой угол светила t, который в параллактическом треугольнике всегда является местным часовым углом, связанным с долготой соотношением 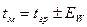(см. далее).

Стороны и углы параллактического треугольника всегда меньше 180°, поэтому входящий в треугольник часовой угол принимается практическим, E или W, а азимут – в полукруговом счете, т.е. также меньшим 180°.

Рис. 3.4.

Значение параллактического треугольника заключается в том, что он связывает горизонтные и экваториальные координаты с географическими места.

Все задачи мореходной астрономии в конечном счете сводятся к решению полярного треугольника, в одной из вершин которого находится наблюдаемое светило.

- решение треугольника относительно высоты светила лежит в основе определения места по наблюдениям высот светил, для этого чаще всего используется формула

,

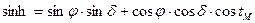откуда видно, что имея высоту, склонение и гринвичский часовой угол и задавшись одной из координат наблюдателя, можно определить другую координату (что впервые сделал Сомнер в 1837 г.);

- решение треугольника относительно азимута светила лежит в основе определения направления истинного меридиана наблюдателя (поправки курсоуказателя), для этого используется формула

,

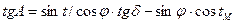откуда видно, что имея координаты светила и наблюдателя, можно вычислить азимут и, сравнив его с наблюденным, определить поправку курсоуказателя;

- решение треугольника относительно местного часового угла светила лежит в основе определения времени наступления различных явлений суточного движения светил, для этого может быть использована формула:

,

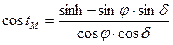откуда видно, что по координатам места наблюдателя, высоте и склонению светила может быть вычислен часовой угол светила, по которому можно определить время наступления интересующего явления.

Взаимное расположение основных кругов и точек на сфере, а также наблюдаемые особенности в движении светил зависят от географической широты наблюдателя. Для того чтобы получить наглядное представление об этих явлениях, принято строить изображение небесной сферы, соответствующее широте наблюдателя. Попутно практикуют приближенное решение задач на преобразование координат светил, т.е. переход от одной системы координат к другой. Построение небесной сферы выполняют от руки, откладывая и снимая координаты "на глаз" с точностью до 5°. Наиболее наглядным и удобными для преобразования координат является перспективное изображение сферы на плоскости меридиана наблюдателя.

Построение сферы начинают с проведения окружности радиусом 5-6 см, которую принимают за меридиан наблюдателя. Проведя вертикальный диаметр, изображающий отвесную линию получают точки Z и n. Перпендикулярно отвесной линии проводят полуденную линию NS и большой круг, изображающий истинный горизонт. Перед тем, как нанести точки N и S, следует по условию задачи определить, какой стороной, восточной или западной, должна быть повернута к нам сфера. Если из наименования практического часового угла или азимута светила следует, что светило находится в восточной половине сферы, то к нам должна быть обращена именно эта половина. В таком случае точку N ставят справа, а S – слева. Если же светило расположено на западной половине сферы, то точку N помещают слева, а S – справа.

От точки N, если широта наблюдателя северная, или S, если широта южная, откладывают в сторону зенита дугу, равную широте j. Отмечают повышенный полюс P_N или P_S, наименование которого одноименно с широтой наблюдателя. Через повышенный полюс и центр сферы проводят ось мира P_NP_S и отмечают пониженный полюс. Перпендикулярно оси мира проводят небесный экватор QQ¢, в точках пересечения которого с истинным горизонтом получают точки E и W.

Построив сферу, наносят светила по заданным координатам и снимают искомые. Линии и дуги, расположенные внутри сферы, или за плоскостью чертежа, изображают пунктиром.

Пример 1. Дано: j = 50°N; А = N 120°W; h = 40°. Построить сферу и определить t и d светила.

Решение:

Строим небесную сферу. Точку N ставим слева, поскольку вторая буква наименования полукругового азимута W и, следовательно, светило расположено в западной половине сферы. Повышенный полюс P_N располагаем под углом 50° над точкой N. Отложив по дуге горизонта заданный А, проводим вертикал светила, откладываем по нему высоту h и наносим светило. Через место светила проводим меридиан и параллель. По экватору от точки Q до меридиана светила измеряем часовой угол t = 40°W, а по меридиану от экватора до места светила – склонение d = 10°N.

Пример 2. j наблюдателя = 30°N; t_W = 300°; t_E = 60°; d = 45°N. Определить h и А этого светила.

Построение сферы и нанесение на нее места светила производятся в следующем порядке:

- произвольным радиусом описывают круг – меридиан наблюдателя;

- проводим отвесную линию и наносим точки зенита Z и надира n;

- проводим большой круг, перпендикулярный отвесной линии – истинный горизонт;

- в точках пересечения истинного горизонта с меридианом наблюдателя наносим точки N (Nord) и S (Sud).

По условию задачи необходимо, чтобы к нам была обращена восточная половина сферы, точка N(Nord) ставится справа.

- по данной широте j = 30°N от точки истинного горизонта, одноименной с широтой, на меридиане наблюдателя откладываем дугу, равную широте, и наносим повышенный полюс P_N;

- от повышенного полюса P_N проводим диаметр (ось мира) и наносим пониженный полюс P_S;

- проводим большой круг, перпендикулярный оси мира P_NP_S – небесный экватор;

- в точках пересечения экватора с меридианом наблюдателя наносим точки:

Q – в полуденной части и Q₁ – в полуночной;

- в точках пересечения небесного экватора с истинным горизонтом наносим Е и W, согласовывая с расположением N;

- по данным координатам наносим место светила С.

Рис. 3.5.

Азимут А и высоту h определяем следующим образом:

1) проводим через точку С вертикал светила, тогда численное значение азимута А определяется дугой Nm = 65°NE, а высоты h – дугой ma = 45°.