Сферические координаты светил

Положение светила на небесной сфере определяется двумя какими-либо сферическими координатами. Существует несколько систем небесных координат; в мореходной астрономии наиболее часто применяются горизонтная и экваториальная (первая и вторая) системы. Каждая система связана с какими-либо основными кругами, от которых отсчитываются координаты.

Горизонтная система координат. Основными кругами для этой системы являются истинный горизонт и меридиан наблюдателя, а координатами – азимут и высота (рис.3.2.).

Рис. 3.2. Рис. 3.3.

Азимутом светила А называется сферический угол при зените, заключенный между меридианом наблюдателя и вертикалом светила. Азимут измеряется дугой истинного горизонта от точки N или S меридиана наблюдателя до вертикала, проходящего через светило.

В мореходной астрономии применяют три системы счета азимута. При полукруговом (астрономическом) счете азимут измеряется от полуночной части меридиана наблюдателя в сторону E или W от 0 до 180°. Точка отсчета полукругового азимута всегда одноименна с наименованием широты наблюдателя, а направление отсчета E или W зависит от того, в какой половине сферы – восточной или западной – находится светило. Полукруговой азимут записывают так, чтобы указать точку и направление отсчета (за рубежом: Z – "азимутальный угол").

Например, на рис. 3.2 у светила С А = N 120° E, или А = 120°NE. При четвертном счете азимут измеряют от точек N или S в сторону E или W от 0 до 90°. Четвертной азимут записывают А = 60°SE.

Круговой азимут измеряется всегда от точки N в сторону E от 0 до 360°. При записи азимута в круговом счете его наименование не указывается: А = 120° (за рубежом – Z_n).

Азимут определяет положение на сфере вертикала светила. Высотой светила h называется угол при центре сферы между плоскостью истинного горизонта и направлением на светило. Высота измеряется дугой вертикала от истинного горизонта до центра светил в пределах от 0 до 90°. Высота считается положительной (+), если светило находится над горизонтом, и отрицательной (-), если светило под горизонтом. В последнем случае высоту называют снижением.

Например, на рис. 3.2 у светила С h = 55°, а у светила С₁ h = -30°.

Если светило находится на меридиане наблюдателя, то его высоту называют меридиональной. Меридиональной высоте приписывают наименование N или S, по той точке горизонта, над которой светило располагается. Например, на рис. 3.2 у светила С₂ H = 25°N.

Вместо высоты иногда применяют ее дополнение до 90°, называемое зенитным расстоянием z. Оно измеряется дугой вертикала от зенита до центра светила в пределах от 0 до 180°. Если светило находится на меридиане наблюдателя, то его зенитное расстояние называется меридиональным Z. Меридиональному зенитному расстоянию приписывают наименование, противоположное наименованию Н.

Между h и Z существует алгебраическая зависимость:

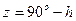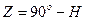; , или ; .

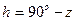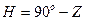Например, на рис. 3.2 у светила С z = 90 – 55 = 35°,

у светила С₁ z = 90 – (30) = 120° и

у светила С₂ Z = 90 – 25 = 65°S.

Высота и зенитное расстояние определяют положение на сфере альмукантарата светила.

Как азимут, так и высота светила непрерывно изменяются вследствие суточного вращения небесной сферы. Эти координаты могут быть измерены с помощью компаса и секстана.

Первая экваториальная система координат. Основными кругами для первой экваториальной системы являются небесный экватор и меридиан наблюдателя, а координатами – часовой угол и склонение (рис. 3.3.).

Часовым углом светила t называется сферический угол при повышенном полюсе между полуденной частью меридиана наблюдателя и меридианом светила. Часовой угол измеряется дугой небесного экватора от полуденной части меридиана наблюдателя до меридиана, проходящего через светило. Применяют две системы счета часовых углов.

Обыкновенный, или вестовый, часовой угол – измеряется от полуденной части меридиана наблюдателя всегда в сторону точки W от 0 до 360°. Такое направление счета соответствует направлению суточного движения светил.

Практический часовой угол измеряется от полуденной части меридиана наблюдателя в сторону точек E или W в пределах от 0 до 180°. Практическому часовому углу приписывается наименование E или W в зависимости от того, в какой половине сферы – восточной или западной – находится светило. При решении задач рекомендуется приписывать наименование также и вестовому часовому углу (за рубежом – меридианный угол).

Вестовый часовой угол, если он превышает 180°, может быть переведен в практический остовый:

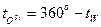
Например, на рис. 3.3 у светила С и C₁ 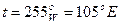. Часовой угол определяет положение на сфере меридиана светила.

Склонением светила d называется угол при центре сферы между плоскостью небесного экватора и направлением на светило. Оно измеряется дугой меридиана светила от экватора до центра светила в пределах от 0 до 90°. Склонению приписывают наименование N, если светило находится в северной половине сферы, и наименование S – если в южной. Например, на рис. 3.3 у светила С d = 55°N, а у светила С₁ d = 27°S.

Вместо склонения иногда применяют его дополнение до 90°, называемое полярным расстоянием D. Оно измеряется дугой меридиана светила от повышенного полюса до центра светила в пределах от 0 до 180° и наименования не имеет.

Между d и D существует алгебраическая зависимость:

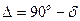или

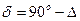
Например, на рис. 3.3 у светила С D = 90 – 55 =35°, а

у светила С₁ D = 90 – (-27) = 117° (наименование склонения светила С₁ разноименно с широтой).

Склонение и полярное расстояние определяют положение на небесной сфере параллели светила.

При суточном движении склонения звезд остаются неизменными, а часовые углы изменяются пропорционально времени. Склонения Солнца, Луны и планет медленно изменяются вследствие их собственного движения.

Вторая экваториальная система координат. Для этой системы основными кругами являются небесный экватор и меридиан точки весеннего равноденствия, а координатами – прямое восхождение и склонение (рис. 3.3.).

Положение на сфере точки весеннего равноденствия, или точки Овна ¡, связано с собственным годовым движением Солнца. В этой точке, расположенной на небесном экваторе, Солнце находится ежегодно » 21 марта (см. далее).

Прямым восхождением a называется сферический угол при полюсе мира между меридианом точки Овна и меридианом светила. Прямое восхождение измеряется дугой небесного экватора от точки Овна до меридиана светила в сторону, обратную счету вестовых часовых углов в пределах от 0 до 360°. Например, на рис. 3.3 для света С a = 50°.

Вторая координата – склонение d - рассмотрена при описании первой экваториальной системы координат.

Особенностью координат второй экваториальной системы a и d является то, то они не зависят от суточного движения светил. Это объясняется тем, что точка Овна участвует в этом движении вместе с другими светилами.