Лекция. «Равенство треугольников» в курсе геометрии 7 класса»

Цель изучения – усвоение учащимися признаков равенства треугольников, формирование умения доказывать равенство треугольников посредством изученных признаков.

Учебник А. В. Погорелова.

1 признак. СМ. «Общую методику»

3 признак.

В1

Дано: DАВС и DА₁В₁С₁.

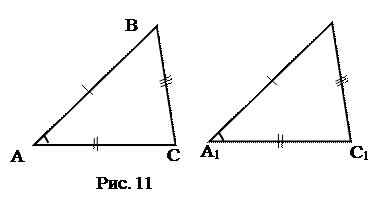
АВ = А₁В₁,

ВС =В₁С₁,

АС =А₁С₁,

Доказать: DАВС = DА₁В₁С₁.

2.По определению равенство треугольников предполагает наличие трёх пар равных элементов, признак сокращает их в 2 раза: до трёх пар равных элементов. Теорема играет важнейшую роль в курсе планиметрии, так как доказательство равенства треугольников станет основным методом доказательства.

3. Метод доказательства состоит в рассмотрении третьего треугольника

А₂В₂С₂, равного треугольнику АВС и совпадающего с треугольником А₁В₁С₁.

4.1.Самостоятельное доказательство теоремы учащимися в данном случае невозможно в связи с полным отсутствием опыта и сложностью метода доказательства.

4.2. Алгоритм доказательства:

1. Утверждаем существование треугольника А₂В₂С₂ равного треугольнику АВС и определённым образом расположенного относительно треугольника А₁В₁С₁.

2. Доказываем совпадение треугольников А₂В₂С₂ и А₁В₁С₁.

3. Делаем вывод о равенстве треугольников АВС и А₁В₁С₁

4.3.Доказательство

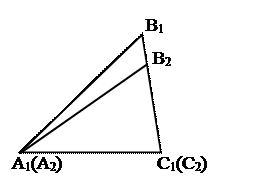
1) По аксиоме VIII существует DА₂В₂С₂=DАВС:

вершина А₂ совпадает с вершиной А₁;

вершина С₂ принадлежит лучу А₁С₁;

вершина В₂ лежит в одной полуплоскости с вершиной В₁ относительно прямой А₁С₁.

	В1

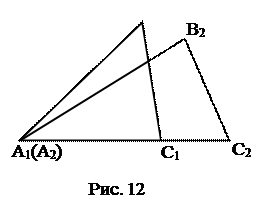
2) Докажем, что вершины С₁ и С₂ совпадают.

А₁С₁ = АС (по условию),

АС=А₂С₂ (так как DА₂В₂С₂=DАВС).

---------------------------------------------------

А₁С₁=А₂С₂.

Следовательно, по аксиоме откладывания отрезков точки С₁ и С₂ совпадают.

Коррекция чертежа.

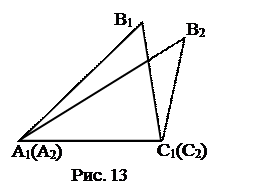
3) Докажем, что точка В₂ принадлежит лучу А₁В₁ или лучу С₁В₁

Метод от противного.

Пусть точка В₂ не принадлежит лучу А₁В₁ и лучу С₁В₁.

Д. П.: В₁В₂, М – середина В₁В₂

АВ= А₁В₁ (по условию)

АВ = А₂В₂ (по определению равных треугольников)

Следовательно, А₁В₁ =А₂В₂. Аналогично, С₁В₁ = С₂В₂.

Тогда DА₁В₁В₂ и DС₁В₁В₂ – равнобедренные. Их медианы являются высотами. То есть А₁М ^ В₁В₂ и С₁М ^ В₁В₂, что противоречит утверждению об единственности перпендикуляра. Утверждение неверно.

Следовательно, точка В₂ принадлежит лучу А₁В₁ или лучу С₁В₁.

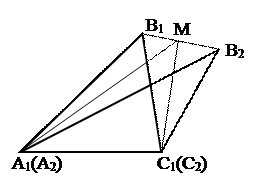
Коррекция чертежа

4) По аналогии с пунктом1 доказываем совпадение вершин В₁ и В₂

Коррекция чертежа.

5) Вывод. По аксиоме о о единственности прямой, проходящей через две точки, треугольники А₂В₂С₂ и А₁В₁С₁ совпали. По сути это два имени одного и того же треугольника. Так как DА₂В₂С₂=DАВС, то и DА₁В₁С₁=DАВС. Что и требовалось доказать.

Вдоказательстве теоремы используется:

· аксиома существования треугольника, равного данному (VIII);

· определение равных треугольников;

· аксиома откладывания отрезков (VI);

· свойство медианы равнобедренного треугольника.

· теорема о единственности прямой, перпендикулярной к данной и проходящей через точку;

· аксиома о единственности прямой, проходящей через две точки (I).

Учебник Л.С. Атанасяна.

Условие и заключение – записаны.

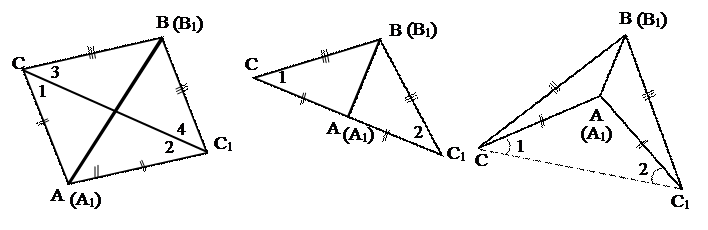
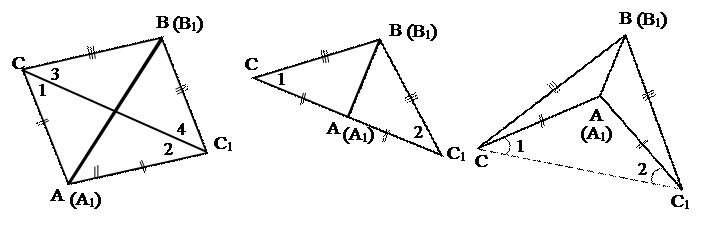
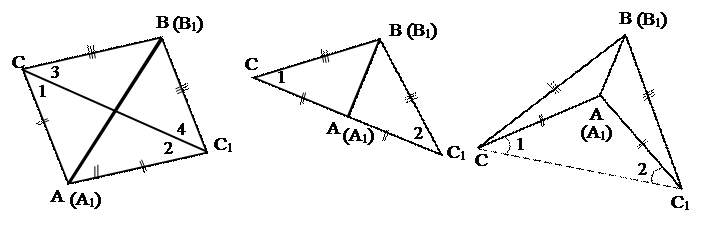
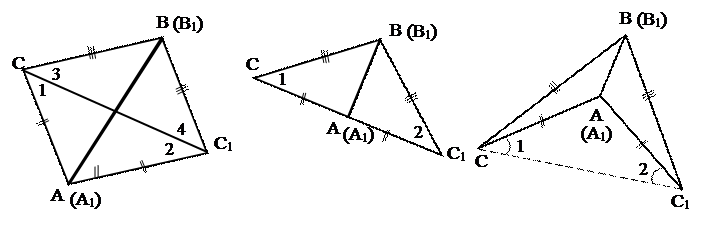
Приложим DАВС к А₁В₁С₁ так, чтобы вершина А совместилась с вершиной А₁, В – с вершиной В₁, а вершины С и С₁ оказались по разные стороны от прямой А₁В₁. Возможны три случая:

1) луч СС₁ проходит внутри угла А₁С₁В₁;

2) луч СС₁ совпадает с одной из сторон угла А₁С₁В₁;

3) луч СС₁ проходит вне угла А₁С₁В₁;

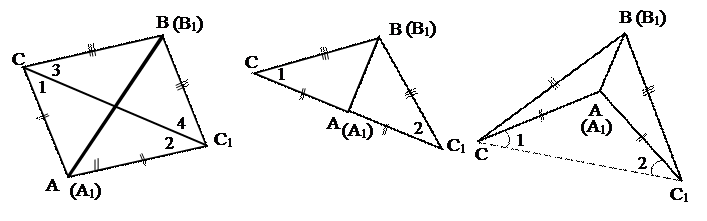
(1) (2) (3)

Рассмотрим случай 1.

Доказательство

1. АС= А₁С₁ (по условию),

СВ= С₁В₁ ( по условию).

Следовательно, DА₁С₁С и D В₁С₁С – равнобедренные.

2. Из (1):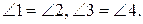

3. Из (2):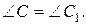

4. 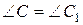(3)

АС= А₁С₁ (условие),

СВ= В₁С₁ (условие).

Следовательно, DАВС = DА₁В₁С₁.

Случаи (2) и (3) доказываются самостоятельно.

Выстраивание цепочки равных треугольников – основной метод доказательства геометрии А. и П. Полезно приучить школьников эвристическому приёму: Если необходимо доказать равенство отрезков или сторон, найди треугольники их содержащие и докажи их равенство.