ДИНАМИКА ИДЕАЛЬНОЙ (НЕВЯЗКОЙ) ЖИДКОСТИ
Основы динамики идеальной жидкости были заложены трудами Эйлера, Бернулли и Даламбера. Эйлером впервые были получены уравнения движения идеальной (невязкой) жидкости. Объектом изучения является модель сплошной жидкости (предложенная Даламбером). Невязкая жидкость - такая, у которой отсутствуют силы вязкости. В то время как для вязкой жидкости напряжения в ней будут состоять из нормальных (давлений) и касательных:
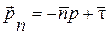 , (1)
, (1)
касательные напряжения, как известно, являются следствием сопротивления жидкости деформациям сдвига. В идеальной жидкости касательные напряжения отсутствуют 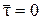 , и так как жидкость выдерживает только сжимающие напряжения, то в ней будут действовать нормальные напряжения или давления
, и так как жидкость выдерживает только сжимающие напряжения, то в ней будут действовать нормальные напряжения или давления

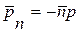 . (2)
. (2)
Уравнения Эйлера и Громеки-Лемба для идеальной жидкости
Для их вывода воспользуемся общим уравнением движения жидкости
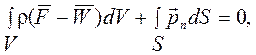 (3)
(3)
принимая во внимание равенство (2) второй интеграл в (3) можно представить следующим образом
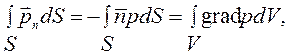 (4)
(4)
тогда уравнение (3) можно записать в следующем виде:
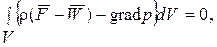 (5)
(5)
что является не чем иным, как интегральной формой записи уравнения движения невязкой жидкости, но дифференциальный объем 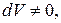 и тогда подынтегральная функция равна
и тогда подынтегральная функция равна
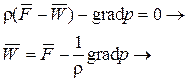
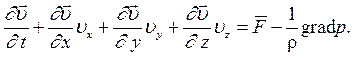 (6)
(6)
Векторное дифференциальное уравнение (6) описывает движение невязкойжидкости. Уравнения Эйлера в проекциях (Декартовы координаты) будут иметь вид :
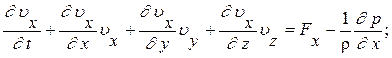
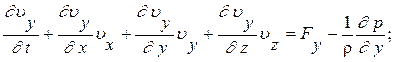
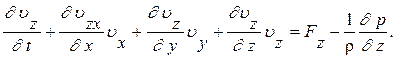 (7)
(7)
В уравнениях (7) неизвестными являются проекции скоростей и давление:
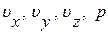 , массовые силы известны (они представлены напряженностями массовых сил). Дополнительным физическим условием является закон сохранения массы, представленный уравнением сплошности
, массовые силы известны (они представлены напряженностями массовых сил). Дополнительным физическим условием является закон сохранения массы, представленный уравнением сплошности
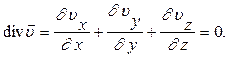 (8)
(8)
Уравнения (7) и (8) образуют замкнутую систему из четырех дифференциальных уравнений в частных производных, которую необходимо интегрировать. Однако, более удобной для интегрирования является форма дифференциальных уравнений, предложенных независимо друг от друга Громека и Лембом. Преобразуем первое уравнение системы (7), тождественно прибавляя и вычитая фрагмент:
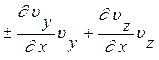 ,
,
получим
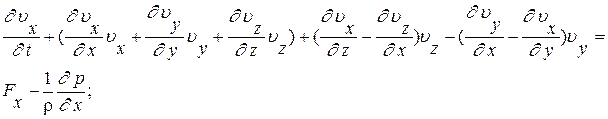 с учетом того, что
с учетом того, что 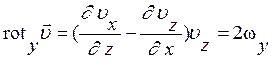 и
и 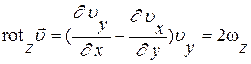 , а также, используя круговую перестановку индексов можно записать два уравнения в проекциях на оси Y и Z :
, а также, используя круговую перестановку индексов можно записать два уравнения в проекциях на оси Y и Z :
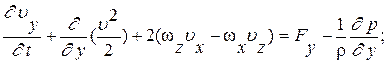
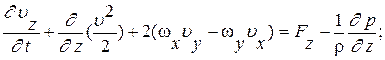
или в векторном виде
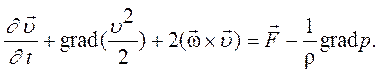 (9)
(9)
Тогда (9) представляет собой дифференциальное уравнение движения невязкой жидкости в форме Громеки-Лемба. В этом уравнении в явном виде выделена компонента 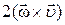 , определяющая величину гидродинамических сил за счет вращения частиц жидкости и физически выражающее Кориолиса ускорение.
, определяющая величину гидродинамических сил за счет вращения частиц жидкости и физически выражающее Кориолиса ускорение.
При интегрировании дифференциальных уравнений движения идеальной жидкости необходимы начальные и граничные условия. Начальные и граничные условия в гидроаэромеханике разделяют на кинематические - относительно поля скоростей и динамические для поля давлений.
Начальные условия. Кинематические и динамические
Должно быть задано поле скоростей в какой-то фиксированный момент времени:
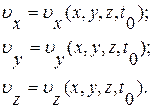
Допустим, что в покоящейся жидкости начинается движение тела из состояния покоя. В момент начала движения скорость движения жидкости в любой ее точке равна нулю
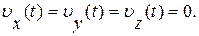
Динамические начальные условия состоят в том, что должно быть задано поле давлений в какой-то фиксированный момент времени
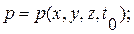
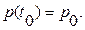
Граничные условия. Кинематические и динамические
Задают поле скоростей на границе, например, на твердой стенке и на бесконечности
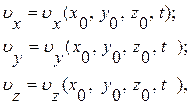
где 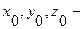 независимые координаты граничной поверхности. Для твердой поверхности граничное условие непроницаемости математически записывают так:
независимые координаты граничной поверхности. Для твердой поверхности граничное условие непроницаемости математически записывают так: 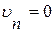 т.е. нормальная компонента скорости равна нулю.
т.е. нормальная компонента скорости равна нулю.
Допустим, что тело движется в безграничной, покоящейся на бесконечности жидкости, тогда
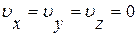 , когда
, когда 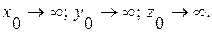
Динамические граничные условия предусматривают задание поля давлений, например, на свободной поверхности и на большом удалении от тела, а именно
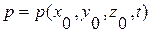 и на свободной поверхности
и на свободной поверхности 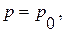 на большом удалении, когда
на большом удалении, когда 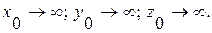
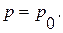
Проинтегрируем уравнение Громеки - Лемба
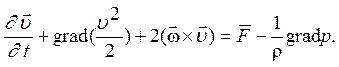
Будем полагать, что массовые силы являются потенциальными:
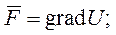
жидкость однородная т.е. 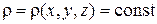 и тогда
и тогда
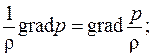
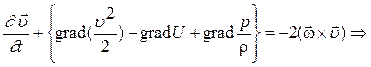
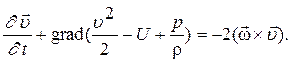 (10)
(10)
Это уравнение Громеки-Лемба (10) для однородного потока идеальнойжидкости, массовые силы которого потенциальны. В качестве дополнительного уравнения необходимо еще уравнение сплошности:
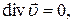 (11)
(11)
Решая совместно систему дифференциальных уравнений (10) и (11) можно определить
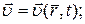
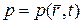 ,
,
где 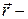 радиус-вектор.
радиус-вектор.
В общем случае система дифференциальных уравнений (10), (11) аналитически не интегрируется, но может быть проинтегрирована с помощью численных методов.
В свою очередь дифференциальное уравнение (10) может быть аналитически проинтегрировано для трех следующих случаев:
1. Потоки стационарные ;
2. Безвихревые потоки;
3. Винтовые потоки.
СТАЦИОНАРНЫЕ ПОТОКИ. ИНТЕГРАЛ БЕРНУЛЛИ
Для стационарных потоков уравнение Громеки-Лемба будет иметь вид:
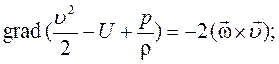 (1)
(1) 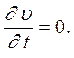
 Проинтегрируем дифференциальное уравнение Громеки-Лемба (1) вдоль
Проинтегрируем дифференциальное уравнение Громеки-Лемба (1) вдоль
линии тока для этой цели правую и левую часть уравнения умножим скалярно на вектор элемента линии тока 
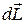 , а затем возьмем интеграл:
, а затем возьмем интеграл:
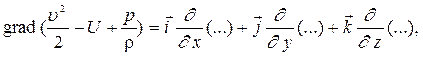
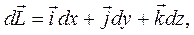
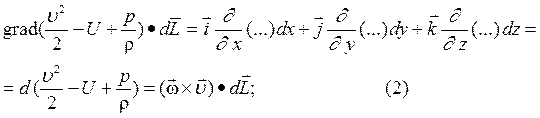
Рассмотрим правую часть уравнения (2)- векторно-скалярное произведение:
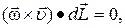 так как
так как 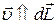 .
.
Тогда полный дифференциал вдоль линии тока (в любой ее точке) равен 0, а именно: 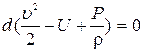 , отсюда интеграл Бернулли будет иметь вид
, отсюда интеграл Бернулли будет иметь вид
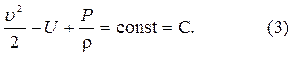
Будем предполагать, что массовыми силами являются гравитационные силы: 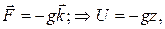 здесь
здесь 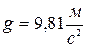 - ускорение свободного падения;
- ускорение свободного падения; 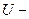 потенциал сил тяжести. Учитывая, выражение для потенциала гравитационных сил, (3) можно записать следующим образом
потенциал сил тяжести. Учитывая, выражение для потенциала гравитационных сил, (3) можно записать следующим образом
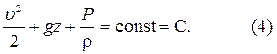
На основании (4) интеграл Бернулли можно представить в двух формах:
1. 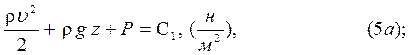
2. 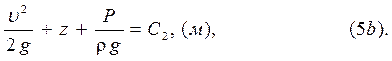
Рассмотрим физический смысл интеграла Бернулли в форме (5а)
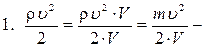 удельная кинетическая энергия; V -объем жидкости;
удельная кинетическая энергия; V -объем жидкости;
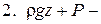 удельная потенциальная энергия.
удельная потенциальная энергия.
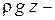 удельная потенциальная энергия положения жидкости;
удельная потенциальная энергия положения жидкости;
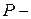 удельная потенциальная энергия давления.
удельная потенциальная энергия давления.
Правая часть интеграла (5а) 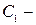 представляет собой полную удельную механическую энергию. Интеграл Бернулли в этой форме позволяет сделать вывод, что вдоль линии тока полная механическая энергия жидкости постоянна (закон сохранения механической энергии вдоль линии тока). Этот вывод справедлив только для идеальной жидкости. Для реальной жидкости часть механической энергии, затрачиваемая на преодоление сил вязкости, переходит в тепловую энергию - диссипация механической энергии.
представляет собой полную удельную механическую энергию. Интеграл Бернулли в этой форме позволяет сделать вывод, что вдоль линии тока полная механическая энергия жидкости постоянна (закон сохранения механической энергии вдоль линии тока). Этот вывод справедлив только для идеальной жидкости. Для реальной жидкости часть механической энергии, затрачиваемая на преодоление сил вязкости, переходит в тепловую энергию - диссипация механической энергии.
Уравнение Бернулли, записанное на основе одноименного интеграла не дает замкнутого решения. Оно лишь позволяет выразить скорость потока через давление и наоборот.
Физическая связь между давлением в потоке и его скоростью, выражаемая интегралом Бернулли используется в современных приборах для измерения скорости потока.
Рассмотрим физический смысл интеграла Бернулли в форме (5b). Все члены, входящие в (5b) имеют линейную размерность и называются высотой или напором:
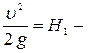 скоростные – высота или напор;
скоростные – высота или напор;
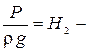 пьезометрические – высота или напор;
пьезометрические – высота или напор;
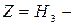 высота или напор – геометрические.
высота или напор – геометрические.
БЕЗВИХРЕВЫЕ ПОТОКИ. ИНТЕГРАЛЫ КОШИ - ЛАГРАНЖА И ЭЙЛЕРА
Безвихревым называют поток, в любой точке которого ротор скорости равен нулю

В этом случае частицы жидкости двигаются поступательно, а условием существования такого течения является выражение.

где 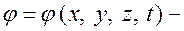 потенциал скорости. При соблюдении условия (2) безвихревые потоки называют еще потенциальными.
потенциал скорости. При соблюдении условия (2) безвихревые потоки называют еще потенциальными.
Воспользуемся уравнением Громеки- Лемба в преобразованном виде:
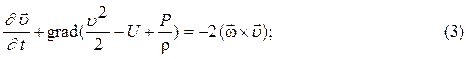
Для потенциальных потоков 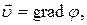 но так как частицы жидкости двигаются только поступательно, то
но так как частицы жидкости двигаются только поступательно, то 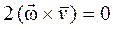 . С учетом сказанного получим:
. С учетом сказанного получим:
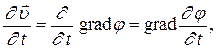 тогда на основании дифференциального уравнения (3) можно записать
тогда на основании дифференциального уравнения (3) можно записать
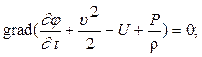 отсюда следует, что
отсюда следует, что
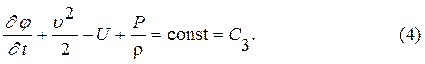
Выражение (4) представляет собой интеграл Коши-Лагранжа для безвихревого потока. С - является постоянной во всех точках потока. Интеграл Коши - Лагранжа для жидкости в поле сил тяжести 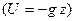 будет иметь вид
будет иметь вид
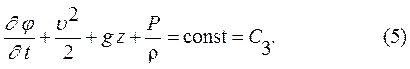
Для стационарных потоков 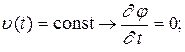 и интеграл Коши-Лагранжа преобразуется в интеграл Эйлера:
и интеграл Коши-Лагранжа преобразуется в интеграл Эйлера:
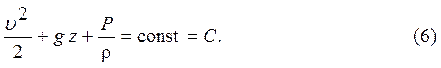
Необходимо отметить, что интеграл Эйлера по написанию с точностью до обозначений не отличается от интеграла Бернулли, но тем не менее между ними есть принципиальное отличие, состоящее в том, что полная удельная механическая энергия (С = const) в интеграле Бернулли постоянна вдоль линии тока, а в интеграле Эйлера постоянна во всем пространстве, которое занимает безвихревой поток.
Как интеграл Эйлера, так и интеграл Коши-Лагранжа не дают замкнутого решения о характеристиках безвихревого потока. Они позволяют только выразить давление через скорость или наоборот. Для безвихревых потоков оказывается возможным получение полного замкнутого решения и фундаментальной задачей таких потоков является интегрирование уравнения Лапласа при заданных начальных и граничных условиях. Тогда, определив потенциал скорости 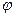 , мы можем определить поле скоростей, а затем, используя интеграл Коши-Лагранжа, определить поле нестационарных давлений
, мы можем определить поле скоростей, а затем, используя интеграл Коши-Лагранжа, определить поле нестационарных давлений 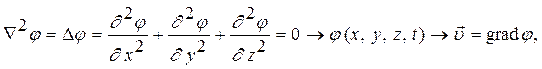
применяя интеграл Коши-Лагранжа 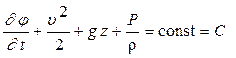 , можно найти поле нестационарных давлений. При интегрировании дифференциального уравнения Лапласа надо знать начальные и граничные условия. Начальные условия определяют потенциал скорости
, можно найти поле нестационарных давлений. При интегрировании дифференциального уравнения Лапласа надо знать начальные и граничные условия. Начальные условия определяют потенциал скорости 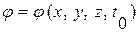 в какой-то момент времени
в какой-то момент времени 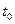 . Например, тело начинает двигаться в покоящейся жидкости из состояния покоя. В этом случае
. Например, тело начинает двигаться в покоящейся жидкости из состояния покоя. В этом случае 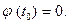
Граничные условия определяют на границах потока:
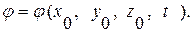 Пример граничных условий - тело из состояния покоя начинает двигаться в покоящейся безграничной жидкости, тогда
Пример граничных условий - тело из состояния покоя начинает двигаться в покоящейся безграничной жидкости, тогда
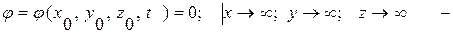 граничное условие на бесконечности;
граничное условие на бесконечности;
На твердой поверхности должно соблюдаться условие непроницаемости, а именно нормальная компонента скорости должна быть равна нулю
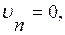 но
но 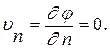
Решение или интегрирование уравнения Лапласа при заданных граничных условиях именуется краевой задачей. Если в качестве граничных условий задан потенциал скорости, то такая задача называется краевой задачей Дирихле. Если же в качестве граничных условий задана производная потенциала 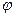 , то задача именуется краевой задачей Неймана.
, то задача именуется краевой задачей Неймана.
В общем случае уравнение Лапласа аналитически не интегрируется. Оно может быть проинтегрировано только для простейших потоков: прямолинейных однородных, источник и сток, плоский вихрь и диполь. Как быть для сложных потоков? Для сложных потоков можно построить приближенное решение, используя принцип суперпозиции (наложение простейших потоков). Правомерность использования этого принципа основана на линейности дифференциального уравнения Лапласа. Для линейного дифференциального известно, что полное решение равно сумме общего решения и частного. Итак, можно записать
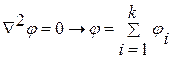 . Дифференциальное уравнение Лапласа разбивается на совокупность дифференциальных уравнений относительно потенциалов простейших потоков
. Дифференциальное уравнение Лапласа разбивается на совокупность дифференциальных уравнений относительно потенциалов простейших потоков
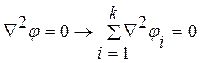
и в конечном итоге решение сводится к решению системы линейных алгебраических уравнений. Такой способ интегрирования уравнения Лапласа является приближенным и относится к категории численных методов. Реализация такого метода возможна только с использованием быстродействующих компьютеров, так как система алгебраических уравнений, описывающих динамику безвихревого течения строго говоря является бесконечной, а приближенность решения состоит в том, что бесконечную систему сводят к конечной. При этом, чем более высокий порядок этой системы, тем точнее описывается динамика безвихревого течения.
3(30).Поясните применение законов количества движения и моментов количества движения к жидкостям.
Одной из важнейших задач гидроаэродинамики является определение суммарного силового воздействия со стороны жидкости на тело. Эта задача может быть решена, если известно распределение напряжений 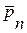 по телу. Однако для определения гидродинамических реакций можно воспользоваться также общими законами механики - законом количества движения и законом момента количества движения.
по телу. Однако для определения гидродинамических реакций можно воспользоваться также общими законами механики - законом количества движения и законом момента количества движения.
Начнем с рассмотрения закона количества движения. Его формулировка известна из механики: производная по времени от вектора количества движения 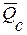 материальной системы равна главному вектору всех внешних сил
материальной системы равна главному вектору всех внешних сил 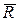 , приложенных к системе:
, приложенных к системе:
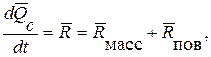
где в случае жидкости 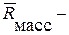 главный вектор массовых сил, а
главный вектор массовых сил, а 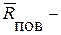 главный вектор поверхностных сил, приложенных на ограничивающих ее объем поверхностях. Отметим, что производную по времени вычисляют в неподвижной системе координат.
главный вектор поверхностных сил, приложенных на ограничивающих ее объем поверхностях. Отметим, что производную по времени вычисляют в неподвижной системе координат.
Выделим в жидкости произвольный жидкий объем V1, ограниченный в начальный момент времени поверхностью S1. Внутри жидкого объема может находиться твердое тело (или тела), ограниченное поверхностью S. Ориентируем внешние по отношению к объему жидкости нормали 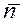 к этим поверхностям. Окончательно выражение закона количества движения можно записать в следующей форме:
к этим поверхностям. Окончательно выражение закона количества движения можно записать в следующей форме:
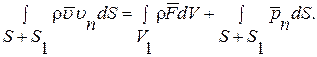
Следует отметить, что это выражение справедливо как для невязкой, так и для вязкой жидкости.
Для невязкой жидкости 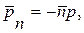 и закон количества движения можно представить в виде
и закон количества движения можно представить в виде
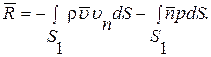
Аналогично может быть получен закон моментов количества движения. Если 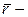 радиус-вектор центра площадки на контрольной поверхности S1, то можно записать
радиус-вектор центра площадки на контрольной поверхности S1, то можно записать
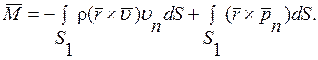
|
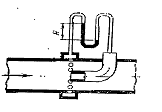
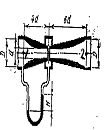
3.Задача 8(2). Найти скорость течения пресной воды на оси трубы, если показания ртутного манометра, подсоединенного к трубке Пито (динамической трубке) и к статическому отверстию равно Н (рис.1)
Рисунок 1. Приемник полного давления трубка Пито (на оси трубы) и U-образный ртутный манометр – для измерения динамического давления
Плотности воды и ртути соответственно
равны: 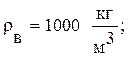
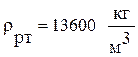 ; H = 0,3 м.
; H = 0,3 м.
Так как такая схема подключения трубки Пито и статического отверстия позволяет измерять динамическое давление:
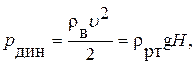 тогда скорость течения найдется из этой
тогда скорость течения найдется из этой
формулы : 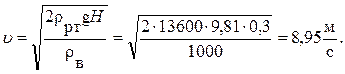
|
3.Задача 7(1).Расход пресной воды плотностью 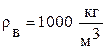 в трубопроводе измеряется с помощью расходомера Вентури (рис. 1). Определить расход воды
в трубопроводе измеряется с помощью расходомера Вентури (рис. 1). Определить расход воды 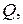 если показание присоединенного к нему ртутного манометра
если показание присоединенного к нему ртутного манометра 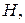 а диаметры широкой и суженной частей расходомера
а диаметры широкой и суженной частей расходомера 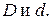 Плотность ртути
Плотность ртути 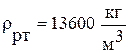 .
.
Рисунок 1. Расходомер Вентури
Вариант 1. 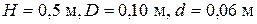 .
.
Выделим линию тока, совпадающую с осью расходомера Вентури. Возьмем на этой линии тока две точки 1 и 2,которые лежат в сечениях проходящих соответственно через широкую часть и узкую. Для этих двух точек запишем уравнение Бернулли:
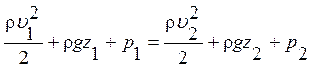 , но так как
, но так как 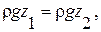 то
то
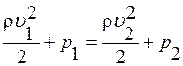 , из этого уравнения Бернулли следует-
, из этого уравнения Бернулли следует-
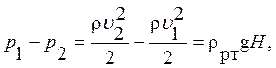 но так как в этом уравнении две неизвестных
но так как в этом уравнении две неизвестных
величины скорости в первом сечении 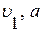 во втором сечении
во втором сечении 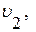 то
то
необходимо дополнительное уравнение и таковым является уравнение расхода 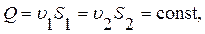 откуда
откуда
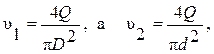 подставив эти выражения для скоростей в исходное уравнение, и разрешив его, относительно расхода
подставив эти выражения для скоростей в исходное уравнение, и разрешив его, относительно расхода 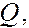 получим:
получим: 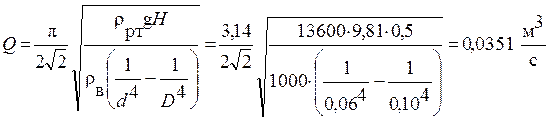 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Cтандарт породы Аляскинский маламут FCI | | | Шариковое дверное подвешивание |
Дата добавления: 2016-08-06; просмотров: 3063;











