Выпуклость, вогнутость, точки перегиба

Определение 4.10. График функции 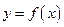называется вогнутым (выпуклым вверх) в интервале (а,b), если он расположен выше касательной, проведенной в любой точке этого интервала (Рис. 4.16 ).

Определение 4.11. График функции 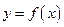называется выпуклым (выпуклым вниз) в интервале (а,b), если он расположен выше касательной, проведенной в любой точке этого интервала (рис. 4.17).

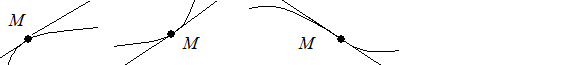
Рис. 4.16 Рис. 4.17 Рис. 4.18

Теорема. Достаточное условие выпуклости (вогнутости) графика функции. Если 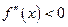в интервале (а,b), то график функции вогнутый в этом интервале; если же 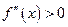, то в интервале (а,b) график функции — выпуклый.

Определение 4.12. Точка 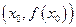графика функции, отделяющая выпуклую его часть от вогнутой, называется точкой перегиба, причем в этой точке должна существовать единая касательная. (Рис. 4.18).

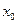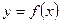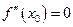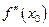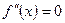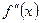Если — абсцисса точки перегиба графика функции , то вторая производная или не существует. Точки, в которых или не существует, называются критическими точками II рода.

Если х₀ — критическая точка II рода и при переходе через эту точку вторая производная меняет знак, то точка 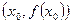является точкой перегиба. Причем в этой точке функция должна быть непрерывной и должна существовать единая касательная. Если вторая производная не меняет знак, то перегиба в данной точке не будет.