Правило Лопиталя раскрытия неопределенностей
Пусть функции f(х) и g(x) дифференцируемы в некоторой окрестности точки 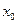 и
и 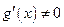 в этой окрестности за исключением точки
в этой окрестности за исключением точки 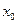 . Если
. Если 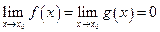 или
или 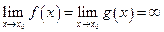 , т. е. отношение этих функций в точке
, т. е. отношение этих функций в точке 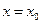 представляет собой неопределенность вида 0/0 или ∞/∞, то
представляет собой неопределенность вида 0/0 или ∞/∞, то
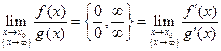
при условии, что существует предел отношения производных. ( 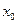 может быть и
может быть и 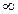 ).
).
Если частное 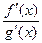 в точке
в точке 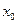 также неопределенность вида 0/0 или ∞/∞ и производные
также неопределенность вида 0/0 или ∞/∞ и производные 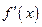 и
и 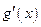 удовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т.д.
удовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т.д.
В случае неопределенности вида 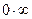 или
или  следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности вида 0/0 или ∞/∞ и далее воспользоваться правилом Лопиталя.
следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности вида 0/0 или ∞/∞ и далее воспользоваться правилом Лопиталя.
В случае неопределенности вида 00, ∞0 или 1∞ следует прологарифмировать данную функцию и найти предел ее логарифма.
Доказывать теорему в общем случае не будем, а ограничимся одним частным случаем, разъясняющим суть дела.
Пусть функции 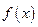 и
и 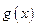 определены и непрерывны в некоторой окрестности точки
определены и непрерывны в некоторой окрестности точки 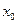 и знаменатель
и знаменатель 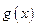 не обращается в нуль в точках этой окрестности, за исключением самой точки
не обращается в нуль в точках этой окрестности, за исключением самой точки 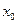 . Пусть
. Пусть 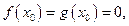 существуют производные
существуют производные 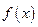 и
и 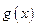 в точке
в точке 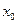 , причем
, причем 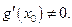 Тогда
Тогда
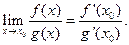
Доказательство. Поскольку 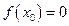 и
и 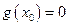 , то
, то
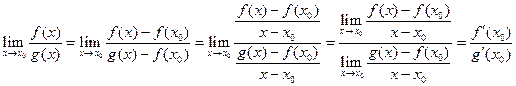 в силу определения производной.
в силу определения производной.
Пример 4. 18.Найти 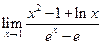 .
.
Решение.Числитель и знаменатель стремятся к нулю при 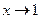 , а потому имеем неопределенность вида 0/0. Воспользуемся правилом Лопиталя, т. е. рассмотрим предел отношения производных заданных функций:
, а потому имеем неопределенность вида 0/0. Воспользуемся правилом Лопиталя, т. е. рассмотрим предел отношения производных заданных функций:
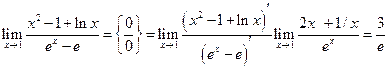 .
.
Пример 4.19.Найти 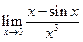 .
.
Решение.Это — неопределенность вида 0/0. Имеем
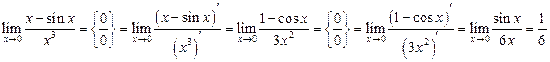 , так как
, так как 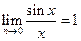 . Здесь правило Лопиталя применено дважды.
. Здесь правило Лопиталя применено дважды.
Пример 4.20.Найти 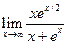 .
.
Решение.В данном случае имеет место неопределенность вида ∞/∞. Находим
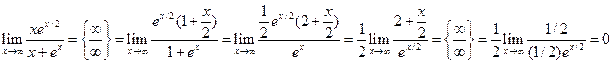 .
.
Пример 4.21.Найти  .
.
Решение.Это — неопределенность вида 0°. Обозначим данный предел через А, т. е. 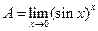 , и прологарифмируем его. Вычислим предел логарифма данной функции, применяя правило Лопиталя (после преобразования к неопределенности вида ∞/∞):
, и прологарифмируем его. Вычислим предел логарифма данной функции, применяя правило Лопиталя (после преобразования к неопределенности вида ∞/∞):
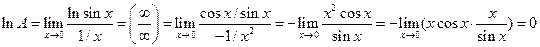 . Следовательно,
. Следовательно, 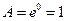 .
.
Дата добавления: 2020-11-18; просмотров: 486;











