Свойства Гауссова клубка
Набор конформаций гибкой макромолекулы в растворе характеризуется гауссовой функцией распределения расстояний между концами цепи: 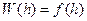 (рис. 13.4.).
(рис. 13.4.).
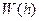 означает вероятность конформации с расстоянием
означает вероятность конформации с расстоянием 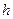 между концами цепи. Согласно формуле Гаусса, эта вероятность определяется выражением:
между концами цепи. Согласно формуле Гаусса, эта вероятность определяется выражением:
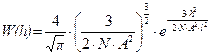 (13.3)
(13.3)

Рис. 13.4. Распределение макромолекул по среднеквадратичным расстояниям между концами цепи.
Анализ этой функции показывает, что сильно свернутые конформации с малым 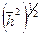 мало вероятны. То же самое можно сказать о сильно вытянутых конформациях со средним значение
мало вероятны. То же самое можно сказать о сильно вытянутых конформациях со средним значение 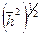 .
.
Молекулярный клубок, характеризующийся гауссовой функцией распределения расстояния между концами цепи, называется гауссовым клубком. Гауссов клубок обладает еще одним свойством, описываемым гауссовой функцией. Плотность сегментов в клубке максимальна в центре, и убывает к периферии и характеризуется гауссовой функцией распределения по радиусу инерции (рис. 13.5).
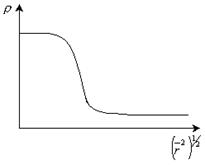
Рис.13. 5. Функция распределения плотности сегментов по радиусу инерции.
Таким образом, гауссов клубок – это облако сегментов, распределенных вокруг центра инерции по гауссову закону. Гауссов клубок имеет форму эллипсоида вращения, близкого к бобу. Следовательно, гауссова функция описывает как множество клубков (по распределению расстояний между концами цепи), так и отдельный клубок (по распределению плотности сегментов относительно центра инерции)
Статистическая теория приводит к простым соотношениям между параметрами, характеризующими размеры цепи, и величиной сегмента: 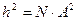 . Если полную контурную длину цепи обозначить через
. Если полную контурную длину цепи обозначить через  , то
, то 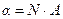 и
и 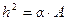 ;
; 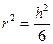 .
.
Эти соотношения справедливы для линейных цепей с гауссовым распределением звеньев при условии 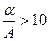 .
.
Дата добавления: 2020-11-18; просмотров: 802;











