Электрокинетические явления.
Вторым основным вопросом этого раздела является 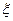 - потенциал. Для его понимания необходимо рассмотреть электрокинетические явления.
- потенциал. Для его понимания необходимо рассмотреть электрокинетические явления.
В электрокинетических явлениях устанавливается взаимосвязь между электрическим полем и движением фаз (твердой и жидкой) относительно друг друга. При наложении внешнего электрического поля возникает движение фаз относительно друг друга. И наоборот, при перемещении фаз возникает разность потенциалов. Переход от движения жидкости к движению взвешенных частиц определяется соотношением объемов фаз и наличием жесткой структуры системы.
Рис. 10.8. Схема электрофореза (  ) и электроосмоса (
) и электроосмоса (  ).
).
Перемещение частиц во внешнем электрическом поле называется электрофорезом. Схема электрофореза, впервые обнаруженного профессором Московского университета Ф.Ф. Рейссом в 1808 г. изображено на рисунке рис. 10.8, 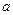 . В мокрую глину помещаются две заполненные водой стеклянные трубки, в которых расположены электроды, и прикладывается внешнее электрическое поле. В анодном пространстве появляется взвесь частиц, движущихся к аноду. Это указывает на то, что частицы глины заряжены отрицательно.
. В мокрую глину помещаются две заполненные водой стеклянные трубки, в которых расположены электроды, и прикладывается внешнее электрическое поле. В анодном пространстве появляется взвесь частиц, движущихся к аноду. Это указывает на то, что частицы глины заряжены отрицательно.
Если в электрическом поле движутся малые ионы, то это явление называется ионной проводимостью, а если крупные частицы или макромолекулы белка – то электрофорезом.
При электроосмосе (рис. 10.8, 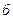 )
) 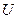 – образная трубка заполняется песком, над которым находится слой воды и прикладывается разность потенциалов. Перемещение жидкости вызывается движением ионов диффузного слоя, которые увлекают всю массу жидкости, заполняющую капилляры воды и поры.
– образная трубка заполняется песком, над которым находится слой воды и прикладывается разность потенциалов. Перемещение жидкости вызывается движением ионов диффузного слоя, которые увлекают всю массу жидкости, заполняющую капилляры воды и поры.
Разность уровней жидкости в катодном и анодном пространстве, называемая электроосмотическим поднятием, может быть очень велика. При 100В значение электроосмотического поднятия достигает 20 см.
При течении жидкости через пористое тело под действием разности давлений возникает явление, называемое потенциалом течения (рис. 10.9, 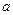 ). Это явление было обнаружено Квинке в 1859 г. Причина его состоит в том, что движущаяся дисперсионная среда увлекает за собой противоионы, что вызывает образование поверхностного электрического тока (ток течения). На концах капиляров возникает разность потенциалов, которая вызывает встречный объемный ток ионов противоположного знака. При установлении потока ионов выравнивается и устанавливается постоянная разность потенциалов, равная потенциалу течения. Потенциал течения - это явление, обратное электроосмосу.
). Это явление было обнаружено Квинке в 1859 г. Причина его состоит в том, что движущаяся дисперсионная среда увлекает за собой противоионы, что вызывает образование поверхностного электрического тока (ток течения). На концах капиляров возникает разность потенциалов, которая вызывает встречный объемный ток ионов противоположного знака. При установлении потока ионов выравнивается и устанавливается постоянная разность потенциалов, равная потенциалу течения. Потенциал течения - это явление, обратное электроосмосу.

Рис. 10.9. Схема потенциала течения ( 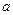 ) и потенциала седиментации (
) и потенциала седиментации ( 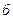 ).
).
Явление, обратное электрофорезу и называемое потенциалом седиментации, было обнаружено Дорном в 1878 г. При седиментации суспензии кварца в центробежном поле он обнаружил возникновение разности потенциалов. Седиментация может происходить под действием как силы тяжести, так и центробежного поля (рис. 10.9, 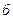 ). При осаждении ионы диффузного слоя вследствие трения отстают от движущейся частицы, что приводит к образованию потока заряженных частиц, и возникновению электрического тока. С помощью электродов, установленных на различной высоте, можно изменить разность потенциалов, т.е. потенциал седиментации. Возникновение потенциала седиментации при оседании частиц, приводит к образованию грозовых разрядов в атмосфере.
). При осаждении ионы диффузного слоя вследствие трения отстают от движущейся частицы, что приводит к образованию потока заряженных частиц, и возникновению электрического тока. С помощью электродов, установленных на различной высоте, можно изменить разность потенциалов, т.е. потенциал седиментации. Возникновение потенциала седиментации при оседании частиц, приводит к образованию грозовых разрядов в атмосфере.
По скорости электрофореза или электроосмоса можно определять 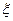 -потенциал. Он расчитывается по уравнению Гельмгольца-Смолуховского, вывод которого приводится ниже.
-потенциал. Он расчитывается по уравнению Гельмгольца-Смолуховского, вывод которого приводится ниже.
10.8. Уравнение Гельмгольца-Смолуховского для определения 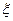 -потенциала.
-потенциала.
Это уравнение позволяет установить связь между скоростью электрокинетических явлений 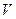 и величиной
и величиной 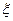 -потенциала
-потенциала 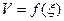 . Уравнение выводится на примере электроосмоса. В основе вывода уравнения лежат следующие предпосылки: ДЭС можно рассматривать как плоский конденсатор, одной обкладкой которого является заряженная поверхность и противоионы до плоскости скольжения, а второй - противоионы диффузного слоя, которые расположены на одинаковом расстоянии от поверхности. Толщина ДЭС много меньше размера частицы, то есть
. Уравнение выводится на примере электроосмоса. В основе вывода уравнения лежат следующие предпосылки: ДЭС можно рассматривать как плоский конденсатор, одной обкладкой которого является заряженная поверхность и противоионы до плоскости скольжения, а второй - противоионы диффузного слоя, которые расположены на одинаковом расстоянии от поверхности. Толщина ДЭС много меньше размера частицы, то есть 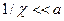 . Твердая поверхность, на которой образован ДЭС, является диэлектриком, а раствор проводит ток. Движение жидкой фазы относительно твердой поверхности ламинарно. Схема конденсатора показана на рис. 10.10.
. Твердая поверхность, на которой образован ДЭС, является диэлектриком, а раствор проводит ток. Движение жидкой фазы относительно твердой поверхности ламинарно. Схема конденсатора показана на рис. 10.10.
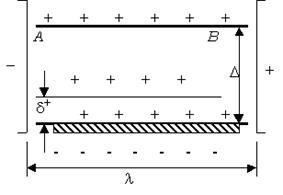
Рис. 10.10. К выводу уравнения Гермгольца-Смолуховского.
Приложим к конденсатору внешнее электрическое поле, потенциал которого равен 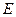 . Если расстояние между электродами равно
. Если расстояние между электродами равно 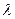 , то напряженность поля
, то напряженность поля 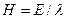 . Под действием внешнего поля противоионы перемещаются к катоду и увлекают за собой жидкость, которая течет вдоль заряженной поверхности. Если обозначить плотность заряда через
. Под действием внешнего поля противоионы перемещаются к катоду и увлекают за собой жидкость, которая течет вдоль заряженной поверхности. Если обозначить плотность заряда через 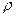 , то электрическая сила
, то электрическая сила 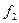 , заставляющая ионы перемещаться, равна
, заставляющая ионы перемещаться, равна 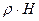 . Эта сила отнесена к 1 см2 поверхности и действует тангенциально к ней.
. Эта сила отнесена к 1 см2 поверхности и действует тангенциально к ней.
Для плоского конденсатора справедливо выражение:
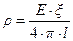 (10.10)
(10.10)
Тогда:
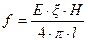 (10.11)
(10.11)
При стационарном режиме течения электрическая сила уравновешивается силой трения 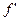 ’.
’. 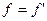 ; По закону Ньютона:
; По закону Ньютона:
 (10.12)
(10.12)
где 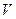 – скорость электрофореза или электроосмоса.
– скорость электрофореза или электроосмоса.
При малом значении 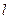 :
:
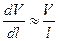 (10.13)
(10.13)
Тогда
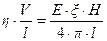 (10.14)
(10.14)
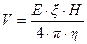 (10.15)
(10.15)
Введем величину 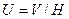 , называемую подвижностью. Она инвариантна по отношению к
, называемую подвижностью. Она инвариантна по отношению к 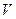 и равна
и равна 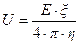 .
.
Дата добавления: 2020-11-18; просмотров: 659;











