Связь поверхностного натяжения с электрическим потенциалом. Уравнение Липпмана.

Поверхностная энергия характеризуется поверхностным натяжением 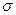, а электрическая энергия поверхности – ее электрическим потенциалом 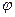. Связь между потенциалом поверхности и величиной поверхностного натяжения описывается уравнением Липпмана. Вывод этого уравнения основан на том, что поверхность раздела фаз представляет собой плоский конденсатор (рис. 10.2), поверхность которого равна 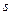, заряд - 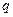, а потенциал - 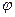. При увеличении поверхности на 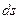заряд увеличивается на .

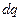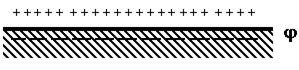
Рис. 10.2. К выводу уравнения Липпмана.

Максимальная изотермическая работа процесса равна изменению свободной энергии:

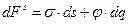(10.1)

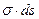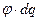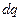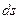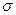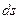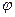где произведение равно работе увеличения поверхности, а величина равна электрической работе. Так как пропорционально , не зависит от , а не зависит от 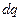, можно проинтегрировать это уравнение, получив:

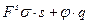(10.2)

Рассмотрим любые возможные изменения системы, то есть получим полный дифференциал 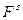, который равен:

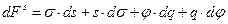(10.3)

Уравнение (10.1) и (10.3) получены независимо и справедливы при условии, что

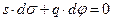(10.4)

Или

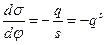(10.5)

Величина 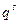называется поверхностной плотностью заряда. Очевидно, что поверхностная плотность заряда определяется зарядом грамм иона и величиной адсорбции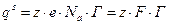

Где 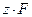– заряд одного грамм иона, 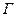– величина адсорбции.

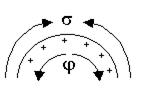
Рис. 10.3. Действие сил поверхностного натяжения и электрических сил на поверхность.

Из этого уравнения следует, что с увеличением потенциала поверхности поверхностное натяжение уменьшается. Физическая сущность этого уравнения заключается в том, что уменьшение свободной поверхностной энергии системы приводит к увеличению электрической энергии. Одноименные заряды стремятся растянуть поверхность, то есть препятствуют поверхностному натяжению, сжимающему поверхность (Рис. 10.3).