Дисперсные системы, подчиняющиеся уравнению Рэлея.

Размер частиц можно определить двумя методами: нефелометрическим и турбидиметрическим. Методом нефелометрии измеряют непосредственно интенсивность света, рассеянного под некоторым углом к падающему лучу света. Методом турбодиметрии измеряют ослабление интенсивности света, проходящего через дисперсную систему. Метод турбидиметрии основан на том, что при прохождении света через коллоидный раствор, содержащий малые прозрачные частицы, поглощение практически отсутствует и ослабление интенсивности падающего света равно полной интенсивности света, рассеянного коллоидным раствором во всех направлениях (полное светорассеяние). Для систем, содержащих частицы с размерами значительно меньше длины световой волны, величина полного светорассеяния подчиняется уравнению Рэлея. В этом случае, измерив фотометром или колориметром ослабление интенсивности падающего света и воспользовавшись уравнением Рэлея, можно определить средний размер частиц.

Рассмотрим поглощение света 1 см³ вещества, то есть 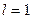, , 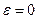тогда уравнение примет вид:

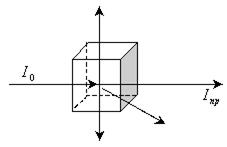
Рис. 9.5.

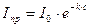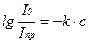; (9.11)

Закон сохранения энергии в данном случае приводит к равенству:

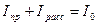(9.12)

где 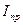, , 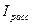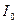– интенсивности соответственно прошедшего, рассеянного и падающего света.

Преобразуем это уравнение, поделив на :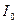

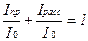(9.13)

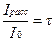(9.14)

где 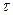– мутность.

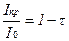(9.15)

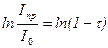(9.16)

С другой стороны 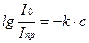, следовательно, 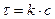(9.17).

Запишем уравнение в общем виде:

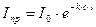
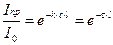
Выразим 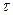через оптическую плотность:

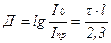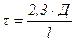; (9.18)

Для дисперсных систем со сферическими частицами уравнение Рэлея можно записать в таком виде:

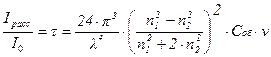(9.19)

где 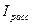- полная интенсивность света, рассеянного 1 см³ системы; 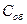– объемная доля дисперсной фазы; 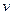– объем частицы, см³.

Отсюда можно вычислить объем частиц:

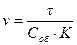(9.20)

где 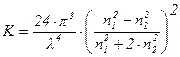(9.21)

Уравнение Рэлея справедливо лишь для разбавленных растворов, так как оно не учитывает вторичного рассеяния света и взаимодействия между частицами. Поэтому для определения размера частиц следует найти 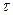для ряда растворов с разной кратностью разбавления и экстраполировать величину 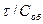до .

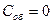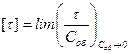(9.22)

Весьма удобным объектом исследования оптических свойств коллоидных систем являются латексы, представляющие модель гидрофобных золей. Они являются двухфазными и трехкомпонентными системами, состоящими из полимерных частиц ультрамикроскопических размеров, взвешенных в серуме – водном растворе стабилизатора. В качестве стабилизатора применяют различные поверхностно-активные вещества (соли жирных и сульфокислот).

9.7.2. Дисперсные системы, не подчиняющиеся уравнению Рэлея.

Интенсивность света, рассеянного разбавленной дисперсной системой, а также угловое распределение рассеянного света (индикатрисса рассеяния) зависят от значений двух безразмерных параметров и 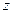. Параметр характеризует отклонение свойств частицы от свойств среды и определяется уравнением

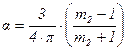(9.23)

где 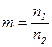- отношение показателя преломления дисперсной фазы к показателю преломления дисперсионной среды.

Параметр 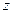характеризует отношение радиуса частицы 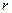к длине волны :

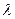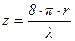(9.24)

Для частиц, размер которых не превышает 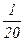длины волны падающего света, при условии отсутствия поглощения света и вторичного светорассеяния справедливо уравнение Рэлея.

Для частиц, размер которых равен длине световой волны или больше ее, определение размеров частиц по светорассеянию может быть осуществлено исходя из общей теории своторассеяния.

В случае, когда радиус составляет от одной десятой до одной третьей длины световой волны, и показатели преломления частиц и среды не слишком различаются ( 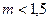), определение размеров частиц дисперсных систем проводят по методу К. С. Шифрина и И. Я. Слонима. Согласно этому методу, мутность зависит от параметров и 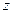следующим образом:

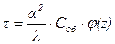(9.25)

а при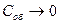

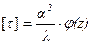(9.26)

где 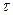– мутность системы, см^-1; 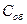– объемная доля дисперсной фазы; 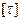– характеристическая мутность.

При 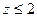(т. е. 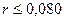) можно использовать уравнение Рэлея (частицы видны в микроскоп).

Зависимость мутности от параметра 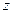описывается уравнением

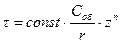(9.27)

Значение показателя степени 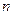в этом уравнении в свою очередь зависит от 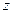; с увеличением 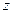значение 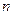уменьшается, стремясь в пределе к 2 для частиц, радиус которых больше длины волны. При малых значениях 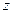соблюдается уравнение Рэлея и при .

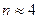Исходя из теории Шифрина, можно определить размер частиц по характеристической мутности. Для этого измеряют значение оптической плотности 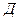серии разбавленных растворов и вычисляют мутность по уравнению:

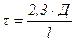(9.28)

С помощью графической экстраполяции находят значение характеристической мутности. Подставляя найденное значение 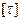, а также значение и 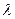в формулу (9.26), определяют значение 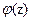и по таблице значение 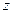. По уравнению (9.24) вычисляют радиус частицы.

С увеличением размеров частиц закон Рэлея перестает соблюдаться и интенсивность рассеянного света становится обратно пропорциональной длине волны в степени меньшей, чем четвертая. Если размер (диаметр) частиц составляет от 1/10 до 1/3 длины световой волны, и показатели преломления частиц и среды не сильно различаются, для описания светорассеяния в системе можно воспользоваться эмпирическим уравнением, предложенным Геллером:

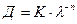и 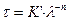(9.29)

где 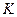и 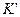– константы, не зависящие от длины волны.

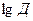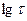Зависимость (или ) от 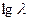в соответствии с уравнением 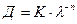и 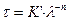представляет собой прямую линию, тангенс угла наклона которой равен показателю степени 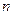с минусом. Значение показателя 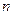в этих уравнениях зависит от соотношения между размером частиц и длиной волны падающего света, характеризуемого параметром .

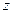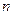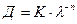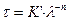Показатель степени в уравнениях и находят на основе турбидиметрических данных. Для этого экспериментально измеряют оптическую плотность системы при различных длинах волн и строят график зависимости в координатах 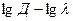. Показатель 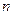определяют по тангенсу угла наклона полученной прямой. По значению 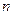находят соответствующее значение параметра 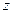, а затем по формуле 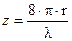рассчитывают средний радиус частиц исследуемой дисперсной системы.

Следует отметить, что этот метод, как и уравнение Рэлея, применим только для «белых» золей, то есть для дисперсных систем, не поглощающих свет (метод базируется только на светорассеянии).