Новый закон формирования средней импульсной электрической мощности
Большая часть электрической энергии с момента начала её применения и по настоящее время генерируется в виде непрерывного напряжения и тока. Эта непрерывность была заложена вначале в алгоритмы, а потом и электронные программы электроизмерительных приборов, учитывающих расход электроэнергии. Когда началось и импульсное использование электрической энергии, то для её учета математики разработали графоаналитический метод, в котором допустили физико-математическую ошибку. Она завышает расход электроэнергии импульсами в количество раз, равное скважности импульсов. Покажем суть этой ошибки и докажем её достоверность теоретически и экспериментально.
Величина, генерируемой и реализуемой электрической мощности, рассчитывается по хорошо известной формуле
 . (286)
. (286)
Математическое содержание этой формулы безупречно, но только при условии непрерывности изменения функций напряжения  и тока
и тока  , например, переменного синусоидального напряжения и тока. Для постоянного напряжения и тока она принимает простой вид
, например, переменного синусоидального напряжения и тока. Для постоянного напряжения и тока она принимает простой вид
 (287)
(287)
и результат расчёта по этой формуле совпадает с показаниями всех приборов (рис. 153). Никаких противоречий в показаниях приборов в этом случае нет.
Введём в схему (рис. 153) электронный ключ 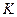 (рис. 153), который будет подавать на клеммы лампочки импульсы напряжения с амплитудами
(рис. 153), который будет подавать на клеммы лампочки импульсы напряжения с амплитудами  , а они будут формировать импульсы тока с амплитудами
, а они будут формировать импульсы тока с амплитудами 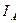 .
.

Рис. 153. Схема для измерения напряжения, тока и мощности,
реализуемой аккумулятором на непрерывное питание лампочки
Чтобы понять физический процесс формирования показаний приборов, запишем осциллограмму на клеммах аккумулятора (рис. 154) и проанализируем процесс формирования средней величины импульсной электрической мощности.
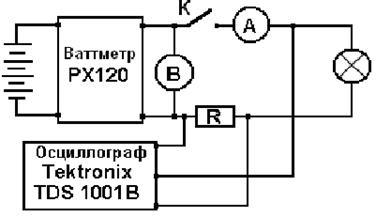
Рис. 154. Схема для измерения напряжения, тока и мощности,
реализуемой аккумулятором на импульсное питание лампочки
Вполне естественно, чтоформула (286) неспособна рассчитать среднюю мощность  , реализуемую аккумулятором не непрерывно, а импульсами, так как при импульсном потреблении электроэнергии функции напряжения
, реализуемую аккумулятором не непрерывно, а импульсами, так как при импульсном потреблении электроэнергии функции напряжения  и тока
и тока  в формуле (286) теряют свой аналитический вид непрерывных функций. В результате полностью исключается возможность аналитического расчёта величины мощности по этой формуле.
в формуле (286) теряют свой аналитический вид непрерывных функций. В результате полностью исключается возможность аналитического расчёта величины мощности по этой формуле.
На осциллограмме (рис. 155) явно видны прямоугольные импульсы напряжения и тока длительностью 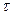 , которая значительно меньше длительности периода
, которая значительно меньше длительности периода 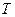 .
.
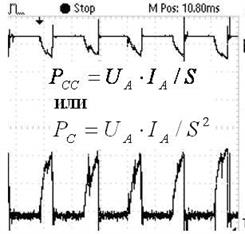
Для определения средней величины импульсной мощности математики разработали графоаналитический метод, основанный на графическом решении уравнения (286).. Этому способствовали возможности современных приборов представлять графически закономерности изменения напряжения и тока (рис. 155).

Рис. 155. Осциллограмма, снятая с клемм аккумулятора, питавшего лампочку импульсами напряжения  и тока
и тока 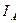
Однако, перевод аналитического метода решенияуравнения (286) в графоаналитический требовал основательных знаний по физике и, особенно по электротехнике, которых у математиковне оказалось. Они не задумывались о физической сути процесса генерации средней величины импульсной мощности. В результате физико-математическая ошибка, допущенная математиками и не обнаруженная инженерами-электриками, задержала развитие экономной импульсной энергетики почти на 100лет. Вот суть этой ошибки.
При составлении программы для графоаналитического решения уравнения (286) с целью определения средней величины импульсной мощности  , реализуемой первичным источником питания, в данном случае, - аккумулятором, роль ориентира выполняло математическое уравнение (286), которое предназначено для вычисления средней мощности, генерируемой непрерывно меняющимися функциями напряжения
, реализуемой первичным источником питания, в данном случае, - аккумулятором, роль ориентира выполняло математическое уравнение (286), которое предназначено для вычисления средней мощности, генерируемой непрерывно меняющимися функциями напряжения  и тока
и тока  . В формуле (286) перемножаются результаты интегрирования функций напряжения и тока. При графоаналитическом методе решения этого уравнения перемножаются ординаты напряжения и тока. Затем полученные произведения складываются и делятся на общее количество произведений в интервале периода
. В формуле (286) перемножаются результаты интегрирования функций напряжения и тока. При графоаналитическом методе решения этого уравнения перемножаются ординаты напряжения и тока. Затем полученные произведения складываются и делятся на общее количество произведений в интервале периода 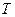 . В результате получается средняя величина электрической мощности
. В результате получается средняя величина электрической мощности 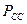 , математическая формула, для расчёта которой принимает вид, представленный в конце формулы (288).
, математическая формула, для расчёта которой принимает вид, представленный в конце формулы (288).
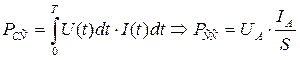 . (288)
. (288)
Символ  в формуле (288) – скважность импульсов. Если импульсы напряжения и тока прямоугольные, то скважность определяется путём деления периода
в формуле (288) – скважность импульсов. Если импульсы напряжения и тока прямоугольные, то скважность определяется путём деления периода 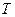 следования импульсов на их длительность
следования импульсов на их длительность 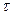 (
( 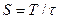 ). Проследим за процессом появления в знаменателе формулы (288) математического символа
). Проследим за процессом появления в знаменателе формулы (288) математического символа  - скважности импульсов.
- скважности импульсов.
Электроника, реализующаяматематические программы, заложенные в современные электронные электроизмерительные приборы, способна измерять в секунду десятки тысяч ординат функций напряжения и тока, перемножать их и выдавать средние значения напряжения, тока и мощности с большой точностью. Проследим, как они делают это. Для этого внимательно присмотримся к осциллограмме на рис. 155. Измеряется ордината импульса напряжения 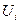 и ордината импульса тока
и ордината импульса тока 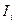 . Затем они перемножаются, полученные произведения складываются, и учитывается общее количество полученных произведений в интервале периода
. Затем они перемножаются, полученные произведения складываются, и учитывается общее количество полученных произведений в интервале периода 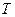 . Вот тут и начинается процесс формирования физико-математических ошибок. Когда ординаты напряжения и тока снимаются в интервале длительности их импульсов
. Вот тут и начинается процесс формирования физико-математических ошибок. Когда ординаты напряжения и тока снимаются в интервале длительности их импульсов 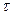 , то физико-математические законы не нарушаются, так как процесс генерирования напряжения и тока в интервале длительности импульса непрерывный. Как только закончился интервал
, то физико-математические законы не нарушаются, так как процесс генерирования напряжения и тока в интервале длительности импульса непрерывный. Как только закончился интервал 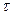 длительности импульса, то ток исчезает из электрической цепи и процесс генерирования мощности, реализуемой аккумулятором, прекращается до следующего импульса.
длительности импульса, то ток исчезает из электрической цепи и процесс генерирования мощности, реализуемой аккумулятором, прекращается до следующего импульса.
А теперь обратим внимание на главное (рис. 155). После прекращения действия импульса тока с амплитудой 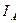 , напряжение на клеммах аккумулятора не падает до нуля, а восстанавливается до своего номинального значения и прекращает своё участие в процессе генерации средней величины импульсной мощности
, напряжение на клеммах аккумулятора не падает до нуля, а восстанавливается до своего номинального значения и прекращает своё участие в процессе генерации средней величины импульсной мощности  в интервале
в интервале 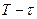 (рис. 155). Но, вольтметр, подключённый к клеммам лампочки, продолжает показывать среднее напряжение на клеммах и лампочки, и аккумулятора, и таким образом - учитывать и ту часть напряжения, которая, остаётся на клеммах аккумулятора, но не участвует в формировании средней величины мощности, когда прерывается импульс, то есть в интервале
(рис. 155). Но, вольтметр, подключённый к клеммам лампочки, продолжает показывать среднее напряжение на клеммах и лампочки, и аккумулятора, и таким образом - учитывать и ту часть напряжения, которая, остаётся на клеммах аккумулятора, но не участвует в формировании средней величины мощности, когда прерывается импульс, то есть в интервале 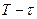 , а формула (288) пытается убедить нас в том, что амплитудное значение напряжения участвует в формировании мощности в интервале всего периода
, а формула (288) пытается убедить нас в том, что амплитудное значение напряжения участвует в формировании мощности в интервале всего периода 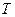 . Программа, продолжает в интервале отсутствия импульсов
. Программа, продолжает в интервале отсутствия импульсов 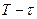 , перемножать нулевые значения ординат тока и полные ординаты номинального напряжения на клеммах аккумулятора. В результате количество произведений с нулевыми значениями тока и не нулевыми значениями напряжения входит в общее количество этих произведений за период
, перемножать нулевые значения ординат тока и полные ординаты номинального напряжения на клеммах аккумулятора. В результате количество произведений с нулевыми значениями тока и не нулевыми значениями напряжения входит в общее количество этих произведений за период 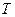 .
.
Далее, программа делит сумму произведений амплитудных значений напряжения и тока, полученных в интервале длительности импульса 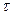 , на общее количество произведений, полученных за весь период
, на общее количество произведений, полученных за весь период 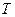 . В итоге получается произведение амплитудных значений напряжения и тока, разделённое на скважность импульсов
. В итоге получается произведение амплитудных значений напряжения и тока, разделённое на скважность импульсов  (см. конец формулы (288). Математики-прикладники,не мудрствуя лукаво, сразу дают, по их мнению, очень убедительную интерпретацию полученному результату
(см. конец формулы (288). Математики-прикладники,не мудрствуя лукаво, сразу дают, по их мнению, очень убедительную интерпретацию полученному результату
 . (289)
. (289)
Они объясняют электротехникам достоверность полученного результата следующим образом. Есть напряжение и ток, есть мощность, нет тока – нет мощности, а величина напряжения, которое присутствует в момент, когда ток равен нулю (в интервале 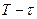 ), не играет никакой роли. С виду, очень убедительное объяснение, а при тщательном анализе – фундаментальная ошибка с глобальными последствиями. Вот её суть.
), не играет никакой роли. С виду, очень убедительное объяснение, а при тщательном анализе – фундаментальная ошибка с глобальными последствиями. Вот её суть.
Система СИ требует непрерывного участия напряжения и тока в формировании мощности в интервале каждого периода, а значит и каждой секунды. Часть  формулы (289) строго соответствует этому требованию, так как из неё следует, средняя величина тока
формулы (289) строго соответствует этому требованию, так как из неё следует, средняя величина тока  , действующего непрерывно в интервале всего периода. Она показана на рис. 155 и равна
, действующего непрерывно в интервале всего периода. Она показана на рис. 155 и равна
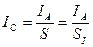 . (290)
. (290)
А теперь посмотрим внимательно ещё раз на осциллограмму (рис. 155) и обратим внимание на физическую суть, содержащуюся в формуле (290). Она заключается в том, что вертикальный прямоугольный импульс тока с амплитудой 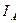 и длительностью
и длительностью 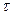 превратился в горизонтальный прямоугольник с амплитудой
превратился в горизонтальный прямоугольник с амплитудой  , заполняющий длительность всего периода
, заполняющий длительность всего периода  . Это полностью соответствует системе СИ, требующей непрерывного участия тока в формировании мощности в интервале всего периода, а значит и – секунды.
. Это полностью соответствует системе СИ, требующей непрерывного участия тока в формировании мощности в интервале всего периода, а значит и – секунды.
Теперь проследим за участием напряжения в формировании средней импульсной мощности. В формуле (289) амплитудное значение напряжения  участвует в формировании средней величины импульсной мощности свей полной величиной
участвует в формировании средней величины импульсной мощности свей полной величиной  в интервале всего периода
в интервале всего периода  , а осциллограмма (рис. 155) отрицает этот факт. Из неё следует, что напряжение со своим амплитудным значением
, а осциллограмма (рис. 155) отрицает этот факт. Из неё следует, что напряжение со своим амплитудным значением  участвует в формировании средней величины импульсной мощности только в интервале длительности импульса
участвует в формировании средней величины импульсной мощности только в интервале длительности импульса 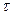 , а во всём остальном интервале
, а во всём остальном интервале 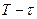 оно не участвует в формировании средней величины импульсной мощности, так как в этом интервале (
оно не участвует в формировании средней величины импульсной мощности, так как в этом интервале ( 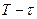 ) цепь разомкнута и на клеммах лампочки нет напряжения. Оно присутствует только на клеммах аккумулятора и равно своему номинальному значению, а в формуле (289) оно участвует своей полной амплитудной величиной
) цепь разомкнута и на клеммах лампочки нет напряжения. Оно присутствует только на клеммах аккумулятора и равно своему номинальному значению, а в формуле (289) оно участвует своей полной амплитудной величиной  в формировании средней величины импульсной мощности весь период
в формировании средней величины импульсной мощности весь период  .
.
В результате этойфизико-математической ошибки величина средней импульсной мощности на питание лампочки, реализуемой аккумулятором, увеличивается в количество раз равное скважности импульсов напряжения. Удивительно то, что этот ключевой момент оказывается непонятным и большинству инженеров-электриков.
Отметим попутно, что описанная ошибка тесно связана с главной аксиомой Естествознания - аксиомой Единства пространства-материи-времени. Ошибочная формула (289) учитывает процесс формирования средней импульсной мощности только в интервале длительности импульса 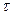 и прекращает этот учет в оставшейся части периода
и прекращает этот учет в оставшейся части периода 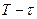 . Это явно противоречит аксиоме Единства, из которой следует, что напряжение и ток должны оставаться функциями времени непрерывно в интервале всего периода формирования мощности. Нельзя останавливать процесс их участия в формировании мощности в заданном интервале времени – секунде, а значит и периода, так как это означает остановку времени участия напряжения в процессе формирования средней величины импульсной мощности. Формула (289) игнорирует это требование аксиомы Единства. В ней правильно
. Это явно противоречит аксиоме Единства, из которой следует, что напряжение и ток должны оставаться функциями времени непрерывно в интервале всего периода формирования мощности. Нельзя останавливать процесс их участия в формировании мощности в заданном интервале времени – секунде, а значит и периода, так как это означает остановку времени участия напряжения в процессе формирования средней величины импульсной мощности. Формула (289) игнорирует это требование аксиомы Единства. В ней правильно  отражён лишь процесс участия тока в формировании средней величины импульсной мощности за весь период. Напряжение же участвует в формировании средней мощности только в интервале длительности
отражён лишь процесс участия тока в формировании средней величины импульсной мощности за весь период. Напряжение же участвует в формировании средней мощности только в интервале длительности 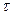 его импульса, а формула (289) убеждает нас, что оно участвует в формировании мощности и в интервале всего периода всей своей амплитудной величиной
его импульса, а формула (289) убеждает нас, что оно участвует в формировании мощности и в интервале всего периода всей своей амплитудной величиной  , что явно ошибочно. Чтобы напряжения
, что явно ошибочно. Чтобы напряжения  , стоящее в формуле (289), также реально участвовало в формировании средней величины импульсной мощности, надо разделить его на скважность импульсов
, стоящее в формуле (289), также реально участвовало в формировании средней величины импульсной мощности, надо разделить его на скважность импульсов  . Тогда, на рис. 155 амплитуда
. Тогда, на рис. 155 амплитуда  импульса напряжения превратится в узкий прямоугольник, растянутый на длительность периода
импульса напряжения превратится в узкий прямоугольник, растянутый на длительность периода 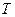 . Это будет означать, что средняя величина напряжения, участвует в формировании средней величины импульсной мощности непрерывно, как это требует аксиома Единства и система СИ. Она меньшей её амплитудной величины в количество раз, равное скважности импульсов
. Это будет означать, что средняя величина напряжения, участвует в формировании средней величины импульсной мощности непрерывно, как это требует аксиома Единства и система СИ. Она меньшей её амплитудной величины в количество раз, равное скважности импульсов  .
.
Ошибочная формула (289) более 100 лет работает во всех электроизмерительных приборах, учитывающих расход электроэнергии, и прочно блокирует процесс разработки экономных импульсных потребителей электроэнергии. Для превращенияошибочной формулы (289) в безошибочную, надо учитывать скважность импульсов тока и импульсов напряжения. В результате имеем
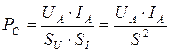 . (291)
. (291)
Результат проведённого анализа настолько очевиден, что нет нужды проверять его достоверность экспериментально, но мы, понимая неизбежность голословных возражений, сделали такую проверку. Взяли аккумулятор, загрузили его импульсным потребителем - электромотором-генератором МГ-2 (рис. 156), который проработал в режиме поочерёдной разрядки одного аккумулятора и зарядки другого 3 часа 10 минут. За это время напряжение на клеммах аккумуляторов упало на 0,3В. Это значит, что при питании электромотора-генератора, который, получая энергию от аккумулятора, часть её передавал электролизёру, а часть - на зарядку другого аккумулятора, скорость падения напряжения на его клеммах оказалась равной 0,1В в час (рис. 156).

Рис. 156. Фото МГ-2 + 2 аккумулятора 6МТС-9 + ячейка электролизёра
Разрядка аккумуляторов за 3 часа 10 минут и осциллограмма напряжения и тока, снятая с клемм аккумулятора, представлены ниже.
| Номера аккумуляторов | Начальное напряжение, В | Конечное напряжение, В | |
| 1+2 (разрядка) | 12,28 | 12,00 | |
| 3+4 (разрядка) | 12,33 | 12,00 | |
3часа 10 минут
|  . .
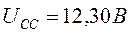 ; ;  ; ;
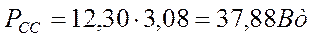 Расчётные данные:
Расчётные данные:
 ; ; 
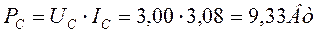 .
Получено 8,57 литров H2+O2 .
Получено 8,57 литров H2+O2
| ||
Рис. 157. Результаты испытаний МГ-2 в режиме разрядки и зарядки аккумуляторов
Расчёт величины средней импульсной мощности, реализуемой аккумуляторами по формуле (289) даёт такой результат
 . (292)
. (292)
В качестве нагрузки, эквивалентной мощности (292), рассчитанной по формуле (289), были взяты лампочки общей мощностью (21+5+5+5)=36,00Вт.Так как из математической модели (289) старого закона формирования средней импульсной электрической мощности следует, что аккумуляторы, питавшие МГ-2, реализовывали мощность равную 37,88Ватт (292), то вместо МГ-2 к тем же аккумуляторам были подключены лампочки с общей мощностью 36Ватт. Начальное напряжение на клеммах аккумуляторов равнялось 12,78В. Через один час 40 минут напряжение на клеммах аккумуляторов упало до 4,86В или на 7,92В. Это в 7,92/0,3=26,00 раз больше скорости падения напряжения на клеммах аккумулятора, питавшего электромотор-генератор МГ-2, без учета разного времени их работы. Если бы лампочки оставались включёнными 3 часа 10 минут, как и при питании электромотора-генератора, то напряжение на клеммах аккумуляторов упало бы до нуля.
Этого вполне достаточно для однозначного вывода о полной ошибочности старого закона (289) формирования средней импульсной электрической мощности и достоверности нового - (291). Конечно, мы не учли 8,57 л смеси водорода и кислорода, полученной путём электролиза воды электрической энергией, вырабатываемой электромотором-генератором. Это, как говорят, дополнительная энергия, которая снижает затраты на получение одного литра водорода и кислорода из воды до 0,60Ватта. Это почти в 5 раз меньше затрат при промышленном получении этой смеси газов.
Второй эксперимент по проверке достоверности формулы (291) и ошибочности формулы (289) длился непрерывно 72 часа. Для его проведения первый электромотор-генератор МГ-1 был переоборудован для питания от 4-х мотоциклетных аккумуляторов (рис. 158). Одна их группа питала МГ-1, а вторая заряжалась импульсами ЭДС индукции статора МГ-1. К импульсам ЭДС самоиндукции статора была подключёна ячейка электролизёра. Схема предусматривала ручное переключение аккумуляторов с режима питания на режим зарядки с интервалом 30мин. В результате были получены данные, представленные в табл. 41.

Рис. 158. Фото МГ-1, ячейки электролизёра и аккумуляторов,
питавших МГ-1 в режиме разрядки и зарядки
Таблица 41. Результаты испытаний МГ-1
| Часы работы | Общее напряжение 1-й группы аккум., В | Общее напряжение 2-й группы аккум., В |
| Через 10 часов | 51,00-49,30 – разрядка | 49,10-51,50– зарядка |
| Через 30 часов | 49,70-48,00 – разрядка | 48,00-50,10 – зарядка |
| Через 60 часов | 48,60-46,10 – разрядка | 48,90-46,10 – разрядка |
| Через 72 часа | 41,80-47,70 – зарядка | 48,20-41,40 – разрядка |
| За 72 часа получено 43 литра смеси газов водорода и кислорода (0,60л/час) |
Таблица 42. Падение напряжения на клеммах аккумуляторов через 72 часа их непрерывной работы в режимах разрядки и зарядки
| Первая группа аккумуляторов | Вторая группа аккумуляторов | ||
| Номер аккум. | Напряж., В | Номер аккум. | Напряж., В |
| 11,03 | 11,40 | ||
| 11,57 | 11,47 | ||
| 7,99 | 10,77 | ||
| 11,64 | 11,74 |
Из табл. 42 следует, что через 72 часа непрерывной работы в режиме разрядка и зарядка напряжения на аккумуляторах № 3 и № 7 опустились ниже допустимой величины 11,00В. В результате время между зарядками и разрядками начало сокращаться и эксперимент был остановлен. Однако его результаты также убедительно свидетельствуют об ошибочности старого закона (289) формирования средней величины импульсной электрической мощности и достоверности нового – (291).
Возникает вопрос о методике составления программы, закладываемой в электроизмерительные приборы, которая автоматически учитывала бы правильно непрерывный и импульсный расход электроэнергии. Для этого надо, чтобы математическая программа, определяющая среднюю величину напряжения, приравнивала нулю ординаты напряжения, соответствующие ординатам тока, равным нулю, и учитывала их количество. Далее, получив сумму ординат напряжения в интервале, например, периода, эта программа, должна делить указанную сумму ординат напряжения на общее количество ординат, в которое входило бы и количество ординат, напряжения которых были приравнены нулю. В результате такой операции при определении средней величины напряжения  автоматически будет учитываться скважность его импульсов, то есть моменты времени, когда ток равен нулю и напряжение не участвует в формировании мощности. Последующее перемножение средних величин напряжения
автоматически будет учитываться скважность его импульсов, то есть моменты времени, когда ток равен нулю и напряжение не участвует в формировании мощности. Последующее перемножение средних величин напряжения  и тока
и тока  , автоматически даст правильную среднюю величину импульсной мощности
, автоматически даст правильную среднюю величину импульсной мощности  , равной величине, определённой по формуле (291). Эта же программа будет правильно учитывать величину электрической мощности при непрерывном процессе подачи напряжения на клеммы потребителя, так как скважность импульсов будет равна
, равной величине, определённой по формуле (291). Эта же программа будет правильно учитывать величину электрической мощности при непрерывном процессе подачи напряжения на клеммы потребителя, так как скважность импульсов будет равна 
Таким образом,ошибочная формула (289), заложенная в математические программы учета электроэнергии, потребляемой из сети, уже более 100лет выполняет роль мощного тормоза в разработке и внедрении импульсных потребителей электроэнергии, так как счётчики, реализующие ошибочную программу, разрабатываемую на основании математической модели (289), завышают реальную величину импульсной мощности в количество раз, равное скважности импульсов напряжения.
В России уже имеются действующие экспериментальные отопительные батареи, потребляющие электроэнергию из сети импульсами со скважностью, равной 100. Существующие счётчики электроэнергии, в которые заложен ошибочный алгоритм или ошибочная программа завышают реальный расход электроэнергии такими батареями в 100 раз и таким образом прочно закрывают им дорогу к потребителю.
Новый закон формирования электрической мощности (291) открывает неограниченные возможности в сокращении расхода электроэнергии путём замены непрерывных потребителей электроэнергии импульсными, при условии замены существующих счётчиков электроэнергии, искажающих учёт её импульсного расхода, новыми, правильно учитывающими величину не только непрерывно, но импульсно потребляемой электроэнергии. Изготовленные и испытанные первые в мире российские электромоторы – генераторы МГ-1, МГ-2 и МГ-3, вырабатывающие и потребляющие электроэнергию импульсами, убедительно доказали достоверность нового закона формирования импульсной электрической мощности (291) и полную ошибочность старого (289).
Представленная здесь методика составления математических программ для счётчиков электроэнергии, правильно учитывающих её импульсное потребление, означает, что российская наука уже открыла путь экономной импульсной энергетике. Следующий шаг должна сделать власть. Информируем её о том, что математикам не составит труда разработать универсальную математическую программу для электронного счётчика электроэнергии, который бы правильно учитывал не только непрерывное, но и импульсное потребление электроэнергии. Изготовив его и испытав, мы откроем путь очень экономным импульсным потребителям электроэнергии.
Уважаемые математики! Сколько лет скрывалась от нас Ваша фундаментальная физическая ошибка? Пора исправлять её. Для этого обращаем Ваше внимание на самый простой случай – потребление электроэнергии из аккумулятора импульсами напряжения и тока (рис. 155, а). Электронная программа, заложенная в осциллограф, чётко учитывает в каждом периоде количество ординат тока, равных его амплитудному значению IA и количество ординат тока, равных нулю. Затем программа разделяет суммарную величину ординат тока на общее количество ординат, измеренных в интервале периода T, и выдаёт среднюю величину тока IC .
Такая же программа, определяющая среднюю величину напряжения (см. рис. 159, а), измерит такое же количество ординат напряжения за период T, сложит эти ординаты и, разделив их сумму на количество ординат, выдаст среднюю величину напряжения UCC (см. рис. 159, а), которое якобы все время участвовало в формировании мощности. Но на рис. 159, а хорошо видно, что величина напряжения UCC участвует в формировании мощности лишь в интервале длительности её импульса τ и не участвует в интервале T-τ. Как же составить математическую программу, обрабатывающую осциллограммы, чтобы она учитывала интервалы T-τ неучастия напряжения в формировании средней импульсной мощности?
Для этого надо, чтобы математическая программа, определяющая среднюю величину напряжения, приравнивала нулю ординаты напряжения, соответствующие ординатам тока, равным нулю, и учитывала их количество. Далее, получив сумму ординат напряжения в интервале, например, периода, эта программа, должна делить указанную сумму ординат на общее количество ординат, в которое входило бы и количество ординат, напряжения которых были приравнены нулю. В результате такой операции при определении средней величины напряжения UC автоматически будет учитываться скважность его импульсов, то есть моменты времени, когда напряжение не участвует в формировании мощности. Последующее перемножение средних величин напряжения UC и тока IC, автоматически даст среднюю величину импульсной мощности PC, равной величине, определённой по формуле (291).
Если осциллограмма тока оказывается сложной, то математической программе, обрабатывающей осциллограмму тока (рис. 159, а), несложно найти среднюю величину тока IC. Такая математическая программа снимает в секунду десятки тысяч ординат, в том числе и с нулевыми значениями тока (см. рис.159, а, интервалы 1, 2, 3….14), а потом общую сумму ординат делит на их количество и получает среднюю ординату или среднюю величину тока IC . Тут проблем нет. Они возникают при составлении программы для определения средней величины напряжения (рис. 159, b), участвующего в формировании средней величины мощности PC.

Рис. 159. а) - осциллограмма тока; b) – осциллограмма напряжения
Программы, обрабатывающие осциллограммы напряжения и тока должны работать синхронно. Программа, обрабатывающая осциллограмму напряжения, должна приравнивать нулю все его ординаты в моменты времени, когда ординаты тока тоже равны нулю. При этом количество ординат напряжения, величины которых приравнены нулю, должно входить в общее количество ординат, измеренных на осциллограмме напряжения за заданный промежуток времени. В результате такая программа учтёт только те ординаты напряжения, которые реально участвуют в формировании мощности вместе с током, то есть в моменты времени, когда ординаты тока не были равны нулю. Деление общей суммы всех ординат напряжения на их общее количество, в которое входит и количество ординат, соответствующих нулевым значениям тока, эквивалентно учёту скважности импульсов напряжения и определению его реальной средней величины UC, участвующей в формировании средней величины импульсной мощности PC , определяемой по формуле (291).
Описанная методика обработки осциллограмм даст реальные средние значения напряжения UC и тока IC, участвующие в формировании импульсной мощности, а перемножение их даёт реальную среднюю величину мощности PC (289). Именно эта величина мощности подлежит оплате потребителем, а не мощность, определённая по формуле (291), как это делается сейчас. Более детальная информация по этой проблеме изложена на сайте http://www.micro-world.su/
На рис. 160, а, b. Показаны две бытовые батареи отопления с площадью излучения тепла, равной около 1,5 кв. метра.
Нагревательным элементом первой батареи (рис. 160) является ТЭН мощностью 1,0кВт, а второй – три последовательно соединённые предплазменные ячейки, которые питаются импульсами напряжения, равными 1000В и импульсами тока, равными 150А. Скважность импульсов напряжения и тока равна S=100 (рис. 161). Это значит, что при длительности эксперимента 5мин.=300с батарея получает энергию 300/100=3с, а 297с не получает её, но существующий счётчик электроэнергии игнорирует это и показывает, что на клеммах батареи средняя величина напряжения в течении 300с была не 1000/100=10В, а 220В, что явно не соответствует реальности.
Выравнивание скорости нагрева батарей осуществлялось путем регулирования напряжения на клеммах батареи со стандартным нагревательным элементом. За 30 минут поверхность обоих батарей нагревалась до 80 град. Мощность на клеммах стандартной батареи бала 880Вт, а средняя мощность на клеммах экспериментальной батареи, определённая по формуле (291), - 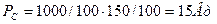 . Столько же потреблял и насос со стиральной машины, прокачивавший жидкость через батарею.
. Столько же потреблял и насос со стиральной машины, прокачивавший жидкость через батарею.

Рис. 160. а) – батарея со стандартным нагревательным элементом;
b) – батарея с тремя экспериментальными ячейками
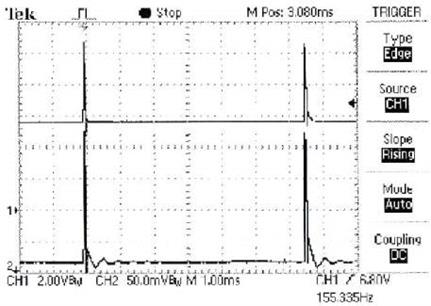
Рис. 161. Импульсы напряжения и тока со скважностью S=100
Что нужно сделать, чтобы начать коммерциализацию этих батарей? Надо, чтобы российская власть приняла решение о разработке универсальных счётчиков энергии, которые бы правильно учитывали не только непрерывное, но и импульсное её потребление, и срочную программу по разработке импульсных потребителей электроэнергии. Это откроет перспективу прекращения строительства атомных электростанций, так как мощности остальных электростанций будут достаточны в условиях широкого внедрения импульсных потребителей электроэнергии.
Новый закон формирования электрической мощности (291) открывает неограниченные возможности в сокращении расхода электроэнергии путём замены непрерывных потребителей электроэнергии импульсными, при условии замены существующих счётчиков электроэнергии, искажающих учёт её импульсного расхода, новыми, правильно учитывающими величину импульсной электроэнергии. Представленная здесь методика составления математических программ для счётчиков электроэнергии, правильно учитывающих её непрерывное и импульсное потребление, означает, что российская наука уже открыла путь экономной импульсной энергетике. Следующий шаг должна сделать власть.
Дата добавления: 2020-11-18; просмотров: 516;











