Геометрические характеристики плоских сечений
Иметь представление о физическом смысле и порядке определения осевых, центробежных и полярных моментов инерции, о главных центральных осях и главных центральных моментах инерции.
Знать формулы моментов инерции простейших сечений, способы вычисления моментов инерции при параллельном переносе осей.
При растяжении, сжатии, смятии и сдвиге деталь сопротивляется деформации всем сечением одинаково. Здесь геометрической характеристикой сечения является площадь.
При кручении и изгибе сечение сопротивляется деформации не одинаково, при расчетах напряжений появляются другие геометрические характеристики сечения, влияющие на сопротивления сечения деформированию.
Статический момент площади сечения
Рассмотрим произвольное сечение (рис. 25.1).
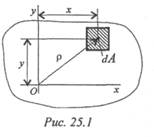
Если разбить сечение на бесконечно малые площадки dA и умножить каждую площадку на расстояние до оси координат и проинтегрировать полученное выражение, получим статический момент площади сечения:
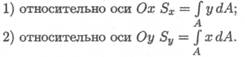
Для симметричного сечения статические моменты каждой половины площади равны по величине и имеют разный знак. Следовательно, статический момент относительно оси симметрии равен нулю.
Статический момент используется при определении положения
центра тяжести сечения:
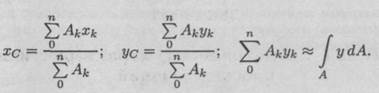
Формулы для определения положения центра тяжести можно записать в виде
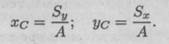
Дата добавления: 2019-02-08; просмотров: 813;











