Условия равновесия плоской системы сходящихся сил в аналитической форме
Исходя из того, что равнодействующая равна нулю, получим:
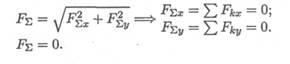
Условия равновесия в аналитической форме можно сформулировать следующим образом:
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской сходящейся системы сил:
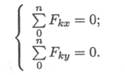
В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
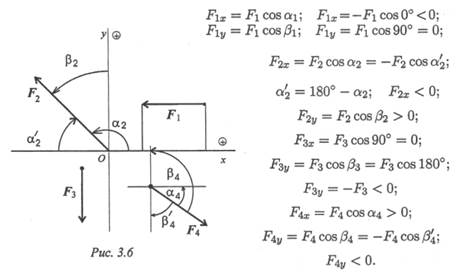
Пример 1.Определить величины и знаки проекций представленных на рис. 3.6 сил.
Решение
Пример 2.Определить величину и направление равнодействующей плоской системы сходящихся сил аналитическим способом.
Решение
1. Определяем проекции всех сил системы на Ох (рис. 3.7а):
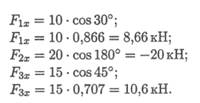
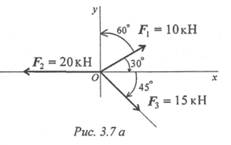
Сложив алгебраически проекции, получим проекцию равнодействующей на ось Ох.
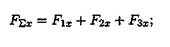
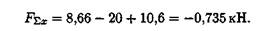
Знак говорит о том, что равнодействующая направлена влево.
2. Определяем проекции всех сил на ось Оу значения проекций, получим величину проекции Оу.
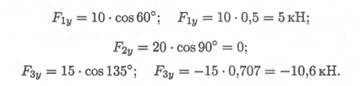
Сложив алгебраически значения проекций, получим величину проекции равнодействующей на ось Оу.
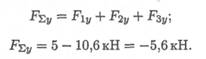
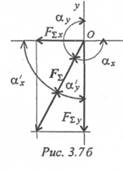
Знак проекции соответствует направлению вниз. Следовательно, равнодействующая направлена влево и вниз (рис. 3.76).
3. Определяем модуль равнодействующей по величинам проекций:
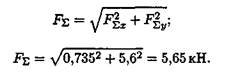
4. Определяем значение угла равнодействующей с осью Ох:
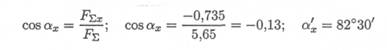
и значение угла с осью Оу:
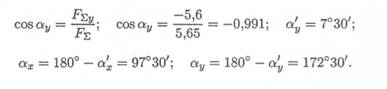
Пример 3.Система трех сил находится в равновесии. Известны проекции двух сил системы на взаимно перпендикулярные оси Ох и Оу:
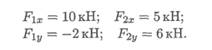
Определить, чему равна и как направлена третья сила системы.
Решение
1. Из уравнений равновесия системы определяем:
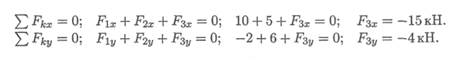
2. По полученным величинам проекций определяем модуль силы:
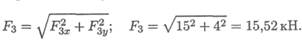
3. Направление вектора силы относительно оси Ох (рис. 3.8):
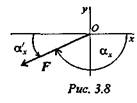
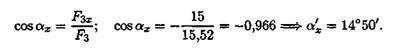
Угол с осью Ох будет равен
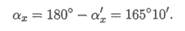
Дата добавления: 2019-02-08; просмотров: 1496;











