Задания для самостоятельного решения
I уровень
1.1. Определите, сколько различных векторов задают упорядоченные пары точек, составленные из вершин:
а) треугольника, б) параллелограмма?
1.2. В плоскости треугольника ABC взята точка О. Отложите от нее вектор:
а) 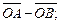 б)
б) 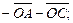 в)
в) 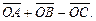
1.3. По заданным векторам 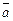 и
и 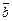 постройте их линейные комбинации:
постройте их линейные комбинации:
а) 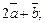 б)
б) 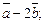 в)
в) 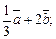 г)
г) 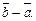
1.4. Вычислите скалярное произведение векторов 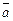 и
и 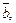 если
если
а) 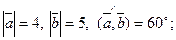 б)
б) 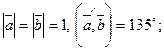
в) 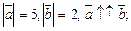 г)
г) 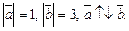
1.5. Зная, что 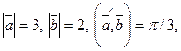 вычислите:
вычислите:
а) 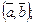 б)
б) 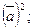 в)
в) 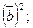 г)
г) 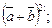 д)
д) 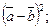 е)
е) 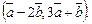
II уровень
2.1. К точке О приложены две силы и 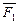 и
и 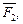 для которых
для которых 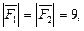 а угол между направлениями этих сил равен 1200. Найдите величину равнодействующей этих сил.
а угол между направлениями этих сил равен 1200. Найдите величину равнодействующей этих сил.
2.2. В треугольнике ABC задается: 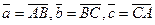 . Точки M, N, P являются серединами сторон BC, AC и AB соответственно. Выразите векторы
. Точки M, N, P являются серединами сторон BC, AC и AB соответственно. Выразите векторы 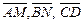 через векторы
через векторы 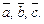
2.3. Определите, на какое число нужно умножить ненулевой вектор 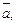 чтобы получить вектор
чтобы получить вектор 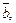 удовлетворяющий следующим условиям:
удовлетворяющий следующим условиям:
а) 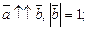 б)
б) 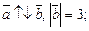
в) 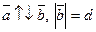 , где
, где 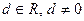 г)
г) 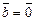 ?
?
2.4. Определите, каким условиям должны удовлетворять векторы 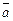 и
и 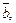 чтобы:
чтобы:
а) 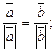 б)
б) 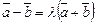 ?
?
2.5. Найдите 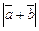 и
и 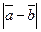 , если векторы
, если векторы 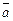 и
и 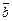 перпендикулярны, причем
перпендикулярны, причем 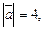
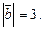
2.6. Вычислите 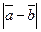 , если
, если 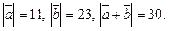
2.7. Вычислите 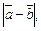 если
если 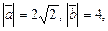
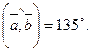
2.8. Найдите длину вектора 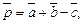 если
если 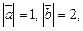
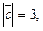
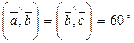 (все векторы лежат в одной плоскости).
(все векторы лежат в одной плоскости).
2.9. Вычислите длины диагоналей параллелограмма, построенного на векторах 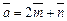 и
и 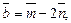 где
где 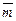 и
и 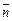 – единичные векторы, угол между которыми 600.
– единичные векторы, угол между которыми 600.
2.10. Найдите 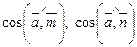 , если
, если 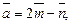 где
где 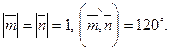
2.11. Определите, какой угол образуют единичные векторы 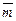 и
и 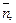 если известно, что векторы
если известно, что векторы 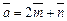 и
и 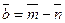 взаимно перпендикулярны?
взаимно перпендикулярны?
2.12. В параллелограмме ABCD длины векторов 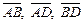 равны соответственно 1, 2, 1. Найдите скалярное произведение векторов
равны соответственно 1, 2, 1. Найдите скалярное произведение векторов 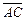 и
и 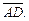
2.13. Найдите угол между векторами 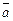 и
и 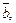 если
если 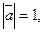
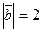 ,
, 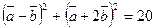 .
.
III уровень
3.1. Точки K, L являются серединами сторон AD и AB параллелограмма ABCD. Полагая 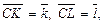 выразите векторы
выразите векторы 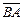 и
и 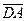 через векторы
через векторы 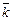 и
и 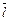 .
.
3.2. В треугольнике ABC проведена биссектриса AD угла A. Найдите разложение вектора 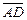 по векторам
по векторам 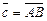 и
и 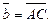
3.3. В параллелограмме ABCD точки M и N являются серединами сторон AD и CD соответственно. Выразите вектор 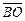 через
через 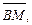 если О – точка пересечения отрезков AN и BM.
если О – точка пересечения отрезков AN и BM.
3.4. Катеты AB и AC прямоугольного треугольника ABC соответственно равны 6 и 8. Найдите косинус угла между векторами 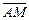 и
и 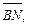 если известно, что AM и BN – биссектрисы углов А и В заданного треугольника.
если известно, что AM и BN – биссектрисы углов А и В заданного треугольника.
3.5. Площадь равнобедренного треугольника равна 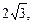 а угол при вершине А – 1200. Найдите скалярное произведение векторов
а угол при вершине А – 1200. Найдите скалярное произведение векторов 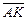 и
и 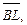 если известно, что K и L – середины соответственно сторон BC и AC треугольника ABC.
если известно, что K и L – середины соответственно сторон BC и AC треугольника ABC.
3.6. Вычислите 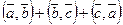 , если
, если 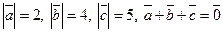 .
.
Дата добавления: 2016-07-27; просмотров: 2069;











