Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Напомним, что термин «линейное уравнение» означает то, что уравнение содержит неизвестную функцию и все ее производные только в первой степени.

Линейным дифференциальным уравнением второго порядка называется уравнение первой степени относительно неизвестной функции и ее производных. Будем записывать его так:

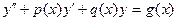(1)

Функции: 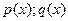- называются коэффициентами данного уравнения, а функция

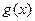- его свободным членом. Если в уравнении (1) его правая часть (свободный член ) равна нулю, то дифференциальное уравнение называется однородным:

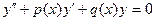(2)

Установим некоторые свойства решений линейного однородного дифференциального уравнения.

Очевидно, что одним из решений уравнения (2) есть : у ≡ 0. Это решение называют нулевым или тривиальным. В дальнейшем, под задачей решения однородного дифференциального уравнения будем понимать задачу отыскания его нетривиальных решений.

Если функции 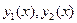- решения уравнения (2), то решением этого уравнения есть также функция:

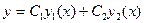(3)

Рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

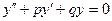(4)

где p,q – действительные числа..

Эйлер предложил искать частные решения этого уравнения в виде

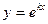(5)

где k – постоянная, которую нужно найти.

Подставив функцию (5) в уравнение (4), получим

,

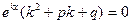Поскольку 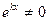, то

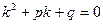(6)

Квадратное уравнение (6) называется характеристическим уравнением дифференциального уравнения (4). Обозначим корни характеристичного уравнения через 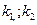и рассмотрим возможные случаи:

1) Если 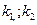- действительные и различные числа, то общее решение уравнения находят по формуле:

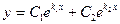(7)

2) Если 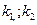- действительные и равные числа, то общее решение уравнения находят по формуле:

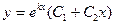(8)

3) Если корни уравнения комплексно-сопряженные 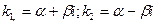, то

общее решение уравнения находят по формуле:

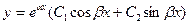(9)