Образец протокола в методе оценки
Протокол № 2
| Показатели | Оценочные категории (k) | Число проб | ||||
Число случаев, когда испытуемый в стимульной пробе выбирал данную оценочную категорию - 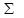 (k/s) (k/s)
| ||||||
Число случаев, когда испытуемый в пустой пробе выбирал данную
оценочную категорию - 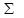 (k/n) (k/n)
| ||||||
Общее число случаев, когда испытуемый выбрал данную категорию: 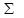 (k/s)+ (k/s)+ 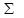 (k/n) (k/n)
|
Протокол №1 метода оценки, в котором фиксируются ответы испытуемого в каждой пробе, не приводится, поскольку он во многом сходен с протоколами в методе «Да-Нет» (см. табл.6 и 7). Отличие протоколов состоит в том, что отсутствует графа «Исход пробы», а в графе «Ответ испытуемого» проставляется номер оценочной категории, которую испытуемый использовал в текущей пробе.
Обработка результатов. Использование нескольких оценочных категорий по сути означает усложнение процесса принятия решений. Для решения поставленной задачи - отнесения результата наблюдения (сенсорного события s) в очередной пробе к той или иной категории из k используемых, испытуемый должен:
1) определить столько значений порога принятия решения λ0, чтобы они позволили разделить все множество сенсорных эффектов s на k классов (областей) – для этого необходимо (k - 1) значений λ0;
2) на оси сенсорных эффектов s, согласно этим значениям λ0, определить (расположить) k - 1 критических значений s0, разделяющих всю ось s на k областей, соответствующих заданным критериям оценок.
На рис.15 приведен пример расположения s0 на оси s при условии
k = 5 в соответствии с теоретическими представлениями, изложенными в разделе 2.2.
Следует отметить, что в реальном эксперименте вряд ли s0 будут располагаться так же равномерно по оси s, однако сути дела это не изменяет.
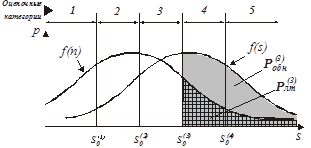
Рис.15. Соотношение распределений плотности вероятности, оценочных категорий и критических значений s0 в теоретической модели метода оценки
Как видно на рис.15, для использования пяти оценочных категорий необходимо разместить на оси сенсорных событий s четыре значения s0 : s0(1), s0(2), s0(3), и s0(4), которые разбивают всю ось s на пять частей, соответствующих числу категорий оценки.
Введем некоторые новые величины, необходимые для дальнейшего рассмотрения метода:
P(k/s) – вероятность того, что сенсорный эффект, вызванный стимулом, отнесен к k-той оценочной категории;
P(k/n) – вероятность того, что сенсорный эффект, вызванный шумом (пустой пробой), отнесен к k-той оценочной категории.
Эти величины рассчитываются следующим образом:
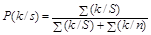 ; (24а)
; (24а)
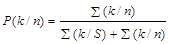 . (24b)
. (24b)
Например, в соответствии с данными, приведенными в таблице 9 для 2-ой оценочной категории, получим:
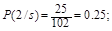
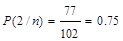 .
.
Проведя соответствующие вычисления для всех категорий, получаем данные, приведенные в табл.10 P(k/s) и P(k/n) для всех пяти значений оценочных категорий.
Таблица 10
Значения P(k/s) и P(k/n) для всех оценочных категорий
| Показатели | Оценочные категории (k) | ||||
| P(k/s) | 0,11 | 0,25 | 0,54 | 0,73 | 0,95 |
| P(k/n) | 0,89 | 0,75 | 0,46 | 0,27 | 0,05 |
Определенные таким образом значения P(k/s) и P(k/n) имеют достаточно простой смысл в графической интерпретации – как площади под соответствующей функцией f(s) или f(n) , взятые от одного значения s0 до другого, и в аналитической – как интегралы этих функций на заданных соседними значениями s0 отрезках s.
По сути дела такой подход означает, что мы пришли к теоретической модели, которая применялась в методе “Да – Нет” при использовании приемов получения нескольких значений λ0 и s0 в нескольких отдельных экспериментальных сериях (см. раздел 2.3.1). теперь эти несколько значений λ0 и s0 мы получаем в одномэксперименте за счет использования нескольких оценочных категорий. Вопрос заключается в том, как по полученным данным рассчитать пары значений Pобн и Pлт, необходимые для построения PX и оценки d¢.
Рассмотрим, как рассчитываются Pобн и Pлт в методе оценки, если в нем используется, например, пять оценочных категорий (как и в примере, приведенном выше). Определим необходимые для этого величины следующим образом:
Ps(k) – вероятность отнесения сенсорного эффекта, вызванного стимулом, в k-ю категорию;
Pn(k) –вероятность отнесения сенсорного эффекта, вызванного пустой пробой, в k -ю категорию.
Тогда значения P(k)обн и P(k)лт, рассчитываемые для соответствующих четырех значений λ0 и s0(k), будут определяться способом, описанным в табл.11.]
Применим теперь подход, изложенный в таблице 11, к экспериментальным данным, содержащимся в таблице 9.
Поскольку число стимульных и пустых проб было равным - по 250, то, учитывая величины 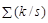 и
и 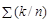 из таблицы (9), получим:
из таблицы (9), получим:
Ps(k)= 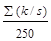 , (25a)
, (25a)
Pn(k)= 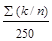 . (25b)
. (25b)
Рассчитанные по формулам (25a,b) значения вероятности обнаружения и ложной тревоги для всех оценочных категорий приведены в табл.12.
Таблица 11
Способ расчета Pобн и Pлт в методе оценки
| Значение s0(k) | Оценочные категории, учитываемые при расчете P(k)обн и P(k)лт | Величины P(k)обн и P(k)лт, ожидаемые согласно теоретическому подходу в методе оценки |
| s0(4) | P(4)обн = Ps(5) P(4)лт = Pn(5) | |
| s0(3) | 5+4 | P(3)обн = Ps(5) + Ps(4) P(3)лт = Pn(5) + Pn(4) |
| s0(2) | 5+4+3 | P(2)обн = Ps(5) + Ps(4) + Ps(3) P(2)лт = Pn(5) + Pn(4) + Pn(3) |
| s0(1) | 5+4+3+2 | P(1)обн = Ps(5) + Ps(4) + Ps(3) + Ps(2) P(1)лт = Pn(5) + Pn(4) + Pn(3) + Pn(2) |
После проведения вычислений получены 5 пар значений Pобн и Pлт, из которых четыре можно использовать для построения PX и расчета d¢. Значения Pобн и Pлт, полученные для 1-ой оценочной категории, в дальнейшем не рассматриваются, так как их величина по определению всегда должна быть равна 1.
Таблица 12
Значения вероятности обнаружения и ложной тревоги для всех s0
| Показатели | Оценочные категории | ||||
| Вероятность отнесения стимула к данной оценочной категории Ps(k) | 0,05 | 0,10 | 0,20 | 0,30 | 0,35 |
| Вероятность обнаружения стимула P(k)обн | 1,00 | 0,95 | 0,85 | 0,65 | 0,35 |
| Вероятность отнесения пустой пробы к данной оценочной категории Pn(k) | 0,39 | 0,31 | 0,17 | 0,11 | 0,02 |
| Вероятность ложной тревоги P(k)лт | 1,00 | 0,61 | 0,30 | 0,13 | 0,02 |
Для построения PX и расчета d¢ переведем нужные величины P(k)обн и P(k)лт в шкалу Z. Результаты пересчета даны в табл.13.
Таблица 13
Значения вероятности обнаружения и ложной тревоги для всех s0
В Z-единицах
| Показатели | Оценочные категории | ||||
| Z(k)обн | - | 1,64 | 1,04 | 0,39 | -0,39 |
| Z(k)лт | - | 0,28 | -0,52 | -1,13 | -2,05 |
Рабочая характеристика, соответствующая данным табл.13, изображена на рис.16 и представляет собой отрезок прямой, проходящий через четыре точки. Определение параметров линейной функции, аппроксимирующей экспериментальные данные, осуществляется по методу наименьших квадратов, описание которого можно найти в любом руководстве по математической статистике.
Поскольку в методе оценки получается несколько пар (точнее – (k – 1) пара) значений Z(k)обн и Z(k)лт (в рассматриваемом примере четыре), то может быть рассчитано и столько же значений показателя чувствительности d¢. В теории или в идеальном эксперименте все эти значения d¢ должны совпасть. Однако в реальном эксперименте этого не происходит. Поэтому в качестве итогового показателя чувствительности может быть взято среднее арифметическое значение всех полученных значений d¢, каждое из которых рассчитывается согласно формуле (23):
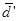 =
= 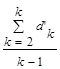 . (26)
. (26)
В примере, согласно данным табл.13, имеем: d¢2 = 1,36; d¢3 = 1,56; d¢4 = 1,52; d¢5 = 1,66, и, соответственно:
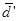 =
= 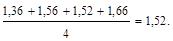
Обращает на себя внимание еще один возможный показатель, который может быть получен в методе оценки – ширина диапазона изменений порогов принятия решения λ0 , возникновение которого обусловлено использованием нескольких оценочных категорий. Это уже характеристика механизмов принятия решения, отражающих психологические особенности личности испытуемого. Косвенно величина этого показателя ( Δλ0 ) может быть оценена через разброс значений Zобн и Zлт для крайних из использованных значений оценочных категорий k.
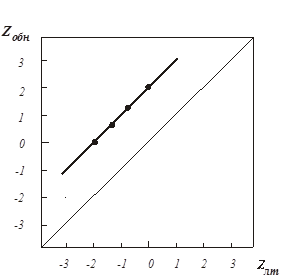 |
Теоретически такой разброс значений должен быть одинаков для Zобн и Zлт – графически (см. рис.16) величина разброса представляет собой расстояние между крайними точками РХ, взятое либо по оси Zобн, либо по оси Zлт. Однако на практике такое равенство встречается редко и является исключением.
Рис.16. РХ, построенная по данным метода оценки
Поэтому можно использовать процедуру приближенного вычисления величины разброса D(λ0), представляющую собой косвенную оценку величины Δλ0:
D(λ0) = [(Z(2)обн – Z(k)обн)+ (Z(2)лт – Z(k)лт)] ∕ 2. (27)
Так, для данных нашего примера:
D(λ0) = [(1,64 – (-0,39))+ (0,28 – (-2,05))] ∕ 2 = 2,18
Значение величины D(λ0), меняющееся в пределах от нуля до шести, позволяет оценить пластичность испытуемого, его способность изменять критерии, используемые при выполнении задания. В определенной степени это значение отражает и готовность испытуемого к применению более рискованной («смелой») стратегии оценивания.
Дата добавления: 2016-07-27; просмотров: 1600;











