Метод вынужденного выбора

Метод вынужденного выбора является самым сложным и трудоемким из описываемых в пособии методов. В связи с этим он и используется реже. Однако его положительной стороной является то, что он позволяет получать более точные и стабильные оценки сенсорной чувствительности, чем другие методы.

Основное отличие от двух предыдущих методов – «Да – нет» и оценивания, где в каждой пробе имелся только один интервал наблюдения (или два, если речь идет об измерении дифференциальной чувствительности), заключается в наличии нескольких таких интервалов. При этом только в одном из интервалов наблюдения предъявляется стимул, а в остальных стимул отсутствует (т.е. остальные пробы пустые). В каком именно интервале наблюдения будет присутствовать стимул, испытуемый не знает. Соответственно задача испытуемого – определить, в каком из интервалов наблюдения – первом, втором, или каком-либо другом был предъявлен стимул.

В другом варианте метода могут использоваться не последовательные интервалы наблюдения, а пространственно разные зоны наблюдения, в одной из которых будет предъявлен стимул. Например, зрительный стимул может предъявляться в левой или правой части экрана или зрительного поля, либо в одной из трех (четырех, пяти, и т.д.) областей экрана, слуховой стимул может быть предъявлен в левое или правое ухо, и т.д.

Главное заключается в том, что и в первом, и во втором вариантах метода вынужденного выбора в каждой пробе стимул обязательно будет предъявлен. Однако где (в какой зоне наблюдения) или когда (в каком интервале наблюдения) это произойдет, испытуемый не знает. Определить этот интервал или зону – задача испытуемого.

Таким образом, основные правила, которые применяются в методе вынужденного выбора, следующие:

1) в эксперименте используется одно значение стимула;

2) в каждой отдельной пробе имеется несколько интервалов (зон) наблюдения (не менее 2-х), в одном из которых предъявляется стимул, а остальные интервалы (зоны) пустые – т.е. без стимула. При этом интервал (зона), в котором появится стимул, выбирается случайным образом и испытуемый не должен знать, в каком из интервалов (зоне) наблюдения ему будет предъявлен стимул.

3) испытуемый должен определить, в каком из интервалов (зоне), по его мнению, был предъявлен стимул, и дать один из ответов:

Ответ R₁ – стимул был в первом интервале (зоне) наблюдения;

Ответ R₂ – стимул был во втором интервале (зоне) наблюдения;

Ответ R_i – стимул был в i-ом интервале (зоне) наблюдения.

Т.е. он должен принять решение, сравнив свои субъективные впечатления, относящиеся к разным интервалам (зонам) наблюдения. При этом испытуемый должен обязательно выбрать один из вариантов ответа – отсюда и название «вынужденный выбор».

Процедура проведения и обработка результатов. Наиболее часто используется самый простой вариант метода вынужденного выбора – двухальтернативный, в котором используется минимальное число интервалов (зон) наблюдения – два. Поэтому дальнейшее описание метода будет относиться именно к такому варианту.

По процедуре проведения метод вынужденного выбора во многом сходен с двумя предыдущими, отличаясь только тем, что в структуре отдельной пробы имеется не один (см. рис.12), а два интервала наблюдения, и в своем ответе испытуемый указывает номер интервала (первый или второй), в котором, по его мнению, присутствовал стимул.

Главное отличие от предыдущих методов состоит в том, как определяются вероятности правильного обнаружения и ложной тревоги - P_обн и P_лт. Обозначим случай, когда стимул предъявляется в первом интервале [sn], а случай, когда стимул предъявляется во втором интервале – [ns]. Испытуемый должен дать один из двух ответов: R₁ – стимул содержится в первом интервале, и R₂ – стимул содержится во втором интервале. Соответственно может быть четыре варианта сочетания ответов и стимульной ситуации:

1) R₁/[sn] – с вероятностью P(R₁/[sn]);

2) R₁/[ns] – с вероятностью P(R₁/[ns]);

3) R₂/[sn] – с вероятностью P(R₂/[sn]);

4) R₂/[ns] – с вероятностью P(R₂/[ns]).

Ответы первого и третьего типов будут правильными, а ответы второго и четвертого типов – ошибочными. Для вероятностей этих ответов справедливы равенства:

P(R₁/[sn]) + P(R₂/[sn]) = 1, (28a)

P(R₁/[ns]) + P(R₂/[ns]) = 1. (28b)

Эти равенства подобны тем, которым подчиняются величины P_обн, P_проп, P_лт и P_отр, и рассматривались ранее (см. равенства (17) в разделе 3.2.3). Поэтому можно взять в качестве аналогов P_обн и P_лт соответствующие величины из равенств (28) - P(R₁/[sn]) и P(R₁/[ns]), считая ответы типа R₁/[sn] случаями правильного обнаружения, а ответы типа R₁/[ns] – ложными тревогами. Такой подход дает возможность использовать данные, получаемые методом вынужденного выбора для построения РХ и вычисления тех же мер чувствительности, что и в предыдущих двух методах – показателя d¢.

Для того, чтобы иметь возможность вычисления этого показателя чувствительности, необходимо данные, полученные при помощи метода вынужденного выбора, привести к общей модели, изложенной в разделе 3.2. Дело в том, что сенсорный эффект при действии стимула (или шума) может появиться как в первом, так и во втором интервале наблюдения. Соответственно будем иметь два стимульных распределения f(s₁) и f(s₂), и два «шумовых» распределения - f(n₁) и f(n₂), где индекс 1 или 2 означает номер интервала наблюдения – первый или второй. То есть в каждом интервале наблюдения испытуемый имеет дело с распределениями f(s) и f(n) (см. разд.3.2.1, 3.2.2 и рис.6). Принимая решение, он должен не только учитывать одно абсолютное значение сенсорного эффекта, но сравнивать величину сенсорного эффекта s₁ в первом интервале наблюдения с величиной сенсорного эффекта s₂ во втором интервале наблюдения. Для ситуации [sn] появление s₁ означает, что сенсорный эффект был вызван стимулом в первом интервале наблюдения, а появление s₂ – что сенсорный эффект был вызван шумом во втором интервале наблюдения (для ситуации [ns] – наоборот).

Это означает, что испытуемый работает при принятии решения с относительными величинами ∆s = s₁ – s₂. Поскольку s₁ и s₂ являются случайными величинами, то и их разность, величина ∆s, также будет случайной. Поскольку s₁ и s₂ еще и независимые величины, то распределения апостериорных плотностей вероятностей того, что стимул был в первом интервале наблюдения (f(∆s /n)), и того, что он был во втором интервале (f(∆s /s)), будут иметь соответственно следующие параметры:

M_n = M_s1 - M_n1, (29a)

M_s = M_s2 - M_n2, (29b)

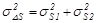. (29c)

Таким образом, мы получаем два новых распределения f(∆s /n) и f(∆s /s), которые располагаются симметрично относительно ∆s= 0, и последующая деятельность испытуемого следует тем же правилам, что описаны в разделе 3.2.

Отметим одну важную особенность метода вынужденного выбора, связанную с симметричностью расположения распределений на оси ∆s. Испытуемый будет стремиться сохранить симметричное относительно ответов R₁ и R₂ значение критерия, подобного s₀ в методе «Да-Нет», что обеспечит высокую стабильность порога принятия решения. Значение критерия ∆s₀, соответствующее такому порогу, выбирается испытуемым близким к точке ∆s = 0. Попытки изменить этот порог с помощью инструкции (например, с помощью изменения стоимостей ответов) в сторону предпочтения одного из ответов, вынуждают испытуемого при попытке следовать такой инструкции давать ответы, которые противоречат результату наблюдения. Как правило, в такой ситуации испытуемый предпочитает опираться на собственные впечатления, игнорируя требования инструкции. Это приводит к высокой стабильности получаемых в итоге результатов и показателей.

Показатель чувствительности 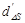в методе вынужденного выбора будет иметь другую величину, чем d’ в методе «Да-Нет» и методе оценки. Пронормировав распределения f(∆s /n) и f(∆s /s) по σ_n = σ_s = 1, с учетом (29) в итоге получаем

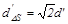, (30)

т.е. чувствительность сенсорной системы по показателю, получаемому в методе вынужденного выбора, оказывается большей, чем в первых двух методах. Такое повышение связано, очевидно, с возможностью для испытуемого сравнивать ощущения из первого и второго интервалов наблюдения, а не опираться при принятии решения только на одну оценку абсолютной величины сенсорного эффекта, как это происходит в методах «Да-Нет» и оценки.

Поскольку критерий, используемый испытуемым в рассматриваемом методе, обладает высокой стабильностью, то построение РХ обычным способом, описанном в 3.3.1, невозможно, так как экспериментальные данные позволяют определить только одну точку РХ, лежащую на пересечении РХ с отрицательной диагональю.

Помимо показателя чувствительности 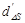, в методе вынужденного выбора используется еще показатель P(C), представляющий собой отношение числа правильных ответов к общему числу проб:

P(C) = P_обн ·P_s + P_отр ·P_n , (31a)

или, учитывая зависимость P_отр от P_лт,

P(C) = P_обн ·P_s + (1 – P_лт) ·P_n . (31b)

Так как P_s и P_n являются на протяжении эксперимента постоянными, то при наличии стабильного критерия и неизменной чувствительности значение P(C) также будет постоянной величиной, изменяясь только тогда, когда меняется чувствительность сенсорной системы.

ЗАКЛЮЧЕНИЕ

Описанные методы представляют собой широкий спектр измерительных процедур оценки чувствительности сенсорных систем человека.

Для получения точных, надежных и устойчивых показателей чувствительности предпочтительным будет использование современных непороговых мер и методов. В наибольшей степени это относится к ситуациям, когда в ходе проведения исследования могут проявляться неконтролируемые исследователем изменения состояний, целей и мотивации испытуемых (либо эти изменения сами являются объектом изучения). Как было показано, именно в этих случаях обнаруживается слабость традиционных пороговых мер чувствительности, приводящая иногда к получению неадекватных результатов. Вместе с тем применение непороговых мер зачастую требует значительных затрат сил и времени, что не всегда оправдано.

Более простые и менее трудоемкие, но менее точные пороговые методы позволяют достаточно быстро и оперативно получить грубую оценку чувствительности, которой в ряде случаев оказывается достаточно для решения поставленных задач, например, в некоторых диагностических задачах, при оценке силы нервной системы, профотборе и т.п. При этом следует иметь в виду интуитивную «понятность» категории «порог чувствительности», что иногда немаловажно с точки зрения доведения полученных результатов до неспециалиста.

Таким образом, рассмотренные методы измерения чувствительности сенсорных систем предоставляют исследователю широкие возможности по выбору конкретного метода в зависимости от целей и задач исследования и имеющихся в его распоряжении ресурсов, позволяя выбрать наиболее оптимальный вариант.

Литература

1. Бардин К.В. Проблема порогов чувствительности и психофизические методы. –М.: Наука, 1973. - 396 с.

2. Гусев А.Н., Измайлов Ч.А., Михалевская М.Б. Измерение в психологии. Общий психологический практикум. –М.: Смысл, 1998.

3. Забродин Ю.М., Фришман Е.З., Шляхтин Г.С. Особенности решения сенсорных задач человеком. –М.: Наука, 1981. – 200 с.

4. Иган Дж. Теория обнаружения сигнала и анализ рабочих характеристик. –М.: Наука, 1983. – 216 с.

5. Проблемы и методы психофизики. /Под ред. А.Г.Асмолова и М.Б.Михалевской. –М.: 1974.

6. Пьерон А. Психофизика. – В кн.: Экспериментальная психология. –М.: Прогресс, 1966, вып. 1. С.241-313.

7. Светс Дж., Таннер В., Бердсолл Т. Статистическая теория решений и восприятие. – В кн.: Инженерная психология. –М.: Сов. радио, 1964. С.269-335.

8. Скотникова И.Г. Психология сенсорных процессов. Психофизика // Современная психология: Справочное руководство. /Под ред.В.Н.Дружинина. М.: Инфра-М, 1999.

9.Энген Т. Психофизика I: Различение и обнаружение. – В кн.: Проблемы и методы психофизики. – М.: Изд-во МГУ, 1964, ч. 1. С.103-173.