Примеры решения задач на взаимодействие распределённых зарядов
1. Прямая бесконечная нить, равномерно заряженная электричеством с линейной плотностью t1 =3×10-7 Кл/м, и отрезок длиной l=20 см, равномерно заряженный электричеством с линейной плотностью t2 =2×10-7 Кл/м, расположены в одной плоскости перпендикулярно друг к другу на расстоянии r0 = 10 см. Определить силу взаимодействия между ними.
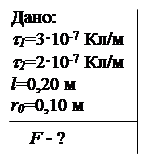
Решение
В задаче рассматривается взаимодействие распределённых зарядов, поэтому для нахождения силы F следует воспользоваться соотношением:
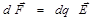 . (1)
. (1)
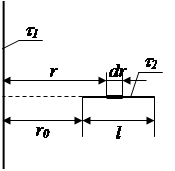 Нить создаёт вокруг себя электростатическое поле, в котором находится заряд, распределённый на отрезке длины l. Если выделить на этом отрезке малый участок длиной dr, то находящийся на нём заряд
Нить создаёт вокруг себя электростатическое поле, в котором находится заряд, распределённый на отрезке длины l. Если выделить на этом отрезке малый участок длиной dr, то находящийся на нём заряд
dq = t2dr (2)
можно считать точечным и рассматривать dF как силу, действующую со стороны электрического поля нити на dq. 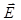 – вектор напряжённости поля нити в месте нахождения электрического заряда dq. Электрическое поле равномерно заряженной нити определяется выражением
– вектор напряжённости поля нити в месте нахождения электрического заряда dq. Электрическое поле равномерно заряженной нити определяется выражением
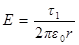 . (3)
. (3)
Выражение (1) можно переписать в скалярной форме, учитывая, что векторы 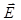 и
и 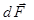 параллельны:
параллельны:
dF = Edq. (4)
Подставив (2) и (3) в (4), получим
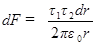 . (5)
. (5)
Для нахождения результирующей силы, действующей на отрезок нити с зарядом q2 со стороны поля прямой бесконечной нити, проинтегрируем выражение (5) в пределах от r0 до (r0+l):
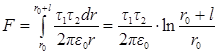 . (6)
. (6)
После подстановки числовых значений получим
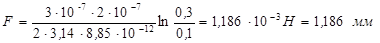 .
.
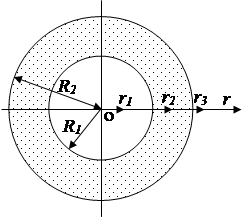
2. Полый стеклянный шар несёт равномерно распределённый по объёму заряд. Его объёмная плотность r=100 нКл/м3. Внутренний радиус шара R1 =5 см, а наружный R2 =10 см. Найти напряжённость электрического поля на расстоянии: а) r1=3 см; б) r2 =6 см; в) r3 =12 см от центра шара.
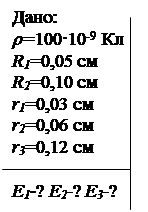
 Решение
Решение
Так как заряд шара распределён в пространстве симметрично относительно центра шара О, то и электрическое поле симметрично относительно этой точки. Это позволяет применить для решения задачи метод Гаусса. Из симметрии задачи следует, что вектор 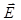 направлен вдоль
направлен вдоль 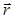 и зависит только от расстояния до центра шара r. Выберем гауссову поверхность в виде сферы, переменного радиуса r с центром в точке О. Учтем, что модуль напряжённости поля шара одинаков во всех точках этой поверхности и Е n= E r. Так как шар диэлектрический, следует применить теорему Гаусса для вектора электрического смещения
и зависит только от расстояния до центра шара r. Выберем гауссову поверхность в виде сферы, переменного радиуса r с центром в точке О. Учтем, что модуль напряжённости поля шара одинаков во всех точках этой поверхности и Е n= E r. Так как шар диэлектрический, следует применить теорему Гаусса для вектора электрического смещения 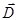 . Тогда поток вектора смещения сквозь гауссову поверхность
. Тогда поток вектора смещения сквозь гауссову поверхность
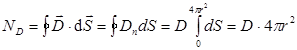 ,
,
где S – площадь гауссовой поверхности, r – её радиус.
Всё пространство можно разбить на 3 области:
1) 0 < r < R1 2) R1 < r < R2 3) r > R2. Применим теорему Гаусса для каждой области.
Для области 0 < r < R1.
Величина свободного заряда, охватываемого поверхностью интегрирования в пределах первой области, равна нулю. Следовательно, поток вектора смещения также равен нулю, а так как площадь поверхности не нулевая, то смещение и напряжённость поля в пределах первой области равны нулю:
D1 = 0, Е1 = D/e0 = 0.
Для области R1 < r < R2.
Свободный заряд, охватываемый гауссовой поверхностью, может быть выражен через объём той части шара, которая попала внутрь сферы радиусом r2:
qсвоб= 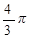 (r23-R13)r.
(r23-R13)r.
Применяя теорему Гаусса, получим
D24pr22 = 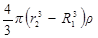 ,
,
E2 = 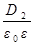 =
= 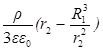 ,
,
где e – диэлектрическая проницаемость стекла.
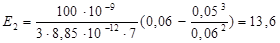 В/м.
В/м.
Для области r > R2.
Внутрь поверхности попадёт весь заряд шара, поэтому
qсвоб = (4/3)p(R23 - R13),
и, применив теорему Гаусса, получим выражение
D3 4pr32 = (4/3) p (R23 - R13)r ;
Е 3 = D 3/e0 = 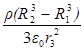 ;
;
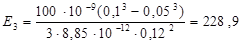 В/м.
В/м.
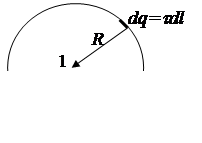
3. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью t=133 нКл/м. Какую работу нужно совершить, чтобы перенести заряд q=6,7нКл из центра полукольца в бесконечность?
Решение
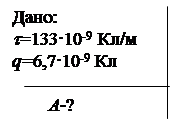
 Работа, совершаемая силами электростатического поля по перемещению заряда из точки 1 в точку 2, может быть выражена по формуле А = q(j1 - j2), где j1 и j2 – потенциалы электрического поля, созданного полукольцом в центре и на бесконечности. Примем j2=0. Тогда
Работа, совершаемая силами электростатического поля по перемещению заряда из точки 1 в точку 2, может быть выражена по формуле А = q(j1 - j2), где j1 и j2 – потенциалы электрического поля, созданного полукольцом в центре и на бесконечности. Примем j2=0. Тогда
А = qj1. (1)
Потенциал j1 найдём, используя принцип суперпозиции для потенциала поля, созданного непрерывно распределёнными зарядами. Для этого разобьем полукольцо на элементарные отрезки длиной dl. Заряд, находящийся на каждом из них, можно считать точечным: dq = tdl. Потенциал поля такого заряда в точке 1
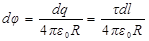 .
.
Интегрируя полученное выражение в пределах от нуля до длины полуокружности l = pR, получим искомый потенциал:
j1= 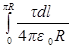 ,
, 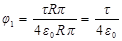 . (2)
. (2)
Подставим уравнение (2) в уравнение (1) и получим
А = qj1 = 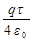 .
.
Подставим числовые значения заданных величин:
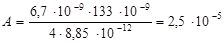 Дж.
Дж.
4. Металлическому шару радиусом R сообщили заряд Q, после этого поверхность шара покрыли слоем диэлектрика толщиной h. Чему равна плотность связанных зарядов на внешней и внутренней поверхностях диэлектрика и полный наведённый заряд, если относительная диэлектрическая проницаемость диэлектрика e.
Решение
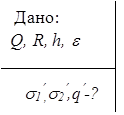 Применим теорему Гаусса для вектора
Применим теорему Гаусса для вектора 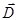 . Поверхность интегрирования выберем в виде сферы с радиусом равным r и центром, совпадающим с центром металлического шара:
. Поверхность интегрирования выберем в виде сферы с радиусом равным r и центром, совпадающим с центром металлического шара:
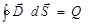 .
.
Ввиду симметрии задачи интеграл в левой части
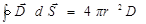 .
.
Сравнивая две формулы, получим выражение для модуля электрического смещения:
D = Q/4pr 2.
С другой стороны, по определению
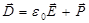 .
.
Используя связь между вектором поляризации и напряженностью электрического поля, запишем
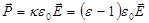 ,
, 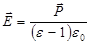 ,
,
где k – восприимчивость диэлектрика.
Подставим это выражение в формулу для электрического смещения
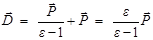 .
.
Учитывая, что векторы 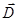 и
и 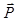 параллельны, и используя результат применения теоремы Гаусса, запишем выражение для модуля вектора поляризации
параллельны, и используя результат применения теоремы Гаусса, запишем выражение для модуля вектора поляризации
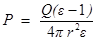 .
.
Вектор 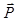 перпендикулярен поверхности диэлектрика и нормальная составляющая вектора поляризации равна поверхностной плотности связанных зарядов:
перпендикулярен поверхности диэлектрика и нормальная составляющая вектора поляризации равна поверхностной плотности связанных зарядов:
P = P n = s¢.
Тогда плотность связанных зарядов на внутренней поверхности диэлектрика рассчитывается при r=(R+0)
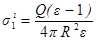 ,
,
и полный заряд, наведенный на внутренней поверхности диэлектрика и связанный с s1¢ соотношением q¢ = 4pR2s1¢
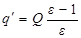 .
.
В силу закона сохранения заряда точно такой же по модулю, но противоположный по знаку заряд должен появиться на внешней поверхности диэлектрика. Очевидно, что его плотность
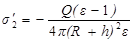 .
.
5. На два последовательно соединенных конденсатора С1 = 100 пФ и С2 = 200 пФ подано постоянное напряжение U = 300 В. Определить энергию, запасенную в каждом конденсаторе.
Решение
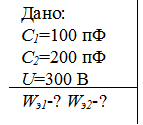 Так как обкладки конденсаторов соединены, то заряд, появляющийся под действием приложенного напряжения на первом конденсаторе, равен заряду, появляющемуся на втором конденсаторе (явление электростатической индукции). Поскольку заряд связан с емкостью конденсатора и напряжением на нем соотношением q = CU, то мы можем записать
Так как обкладки конденсаторов соединены, то заряд, появляющийся под действием приложенного напряжения на первом конденсаторе, равен заряду, появляющемуся на втором конденсаторе (явление электростатической индукции). Поскольку заряд связан с емкостью конденсатора и напряжением на нем соотношением q = CU, то мы можем записать
C 1U 1 = C 2U 2.
С другой стороны,
U 1 + U 2 = U.
Решая совместно эту систему уравнений, найдем напряжение на первом и втором конденсаторе
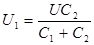 ,
,
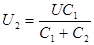 .
.
Подставляя эти значения в формулу для энергии конденсатора, получим
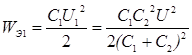 ;
;
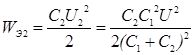 .
.
Подставим значения величин и получим
WЭ1 = 2×10-6 Дж = 2 мкДж, WЭ2 = 1×10-6 Дж = 1 мкДж.
6. Медный проводник (удельное сопротивление меди r = 17 нОм·м) подключен к источнику с ЭДС, e = 4 В. Внутреннее сопротивление источника r = 0,1 Ом. Сечение проводника S = 0,085 мм2, длина l = 9,5 м. Считая, что ток течет по всему поперечному сечению проводника, найти величину напряженности электрического поля внутри него.
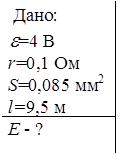 Решение
Решение
Чтобы найти напряженность электрического поля в проводнике, воспользуемся законом Ома в дифференциальной форме:
j = sE,
где j – плотность тока; E – вектор напряженности электрического поля; s – электропроводность вещества проводника, равная 1/r.
Величина искомой напряженности электрического поля в проводнике определяется соотношением:
E = j / s = rj. (1)
Таким образом, задача нахождения напряженности поля сводится к задаче нахождения величины плотности тока j в цепи.
Плотность тока можно найти, если известна сила тока I, протекающего по проводнику
j = I / S. (2)
Полный ток в цепи найдем из закона Ома для полной цепи:
I = e / (R + r), (3)
где r – внутреннее сопротивление источника; R - сопротивление проводника.
Для R справедливо соотношение:
R = rl/S. (4)
Объединяя формулы (1) - (4), окончательно запишем
E = rj = rI / S = re / (R + r)S = re / (rl / S + r)S. (5)
Подстановка в (5) численных данных позволяет написать ответ
Е = 0,4 В/м.
7. Падение напряжения в проводнике, состоящем из двух последовательно соединенных кусков медной проволоки одинаковой длины (l1 = l2 = 10 м), но разного диаметра (d1 = 2d2), равно 10 В. Найти удельную тепловую мощность тока во втором куске проволоки. Удельное сопротивление меди r = 17 нОм·м.
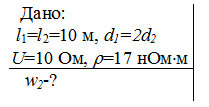 Решение
Решение
Удельная тепловая мощность тока (плотность тепловой мощности)
w = sE 2 = 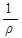 E2 = rj 2.
E2 = rj 2.
Поэтому, чтобы найти w2, необходимо определить две величины: количество теплоты Q2 , которое выделяется в более тонком проводнике в единицу времени, и объем этого проводника.
Количество теплоты Q2 можно найти, если учесть, что ток в проводниках один и тот же, а сопротивления проводников отличаются в 4 раза.
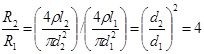 .
.
Согласно закону Джоуля-Ленца, представленному в интегральной форме,
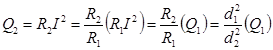 ,
,
где Q1 – тепло, выделяющееся в единицу времени в более толстом проводнике.
Общая энергия, которая выделяется во всем проводнике, рассчитывается по формуле
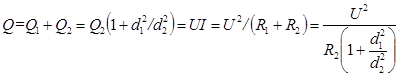 , (1)
, (1)
где U –падение напряжения в проводнике.
Из уравнения (1) следует, что количество теплоты, выделяющееся во втором проводнике в единицу времени,
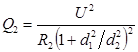 . (2)
. (2)
В уравнении (2) все величины, кроме сопротивления второго участка проводника, известны. Однако в знании R2 нет необходимости. Действительно, если связать между собой объем второго проводника с его сопротивлением
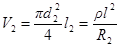 ,
,
то нетрудно видеть, что удельная тепловая мощность тока во втором проводнике не зависит от его сопротивления
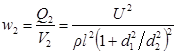 . (3)
. (3)
Подставляя в соотношение (3) численные данные, получаем ответ
w 2 = 3,76×10 7 Вт/м3.
8. Заряд сферического конденсатора из-за того, что через диэлектрическую прокладку протекает ток, уменьшается за время t в n раз. Найти удельное сопротивление r прокладки, если ее диэлектрическая проницаемость равна e.
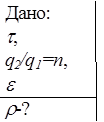 Решение
Решение
Сопротивление диэлектрика между обкладками сферического конденсатора можно найти, просуммировав сопротивления сферических слоев толщиной dr, граничащих друг с другом:
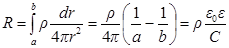 , (1)
, (1)
где a,b – радиусы соответственно внутренней и внешней обкладок сферического конденсатора; e0 – электрическая постоянная; C – емкость сферического конденсатора находится по формуле
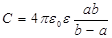 .
.
Из уравнения (1) следует, что для определения величины удельного сопротивления материала прокладки достаточно найти произведение емкости конденсатора на полное сопротивление прокладки:
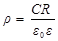 . (2)
. (2)
Это можно сделать, если учесть, что за время dt конденсатор теряет заряд:
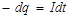 , (3)
, (3)
где I – ток утечки. Знак «-» в (3) учитывает тот факт, что заряд конденсатора со временем убывает.
По закону Ома
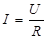 , (4)
, (4)
где U – разность потенциалов между обкладками конденсатора,
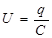 , (5)
, (5)
где q – заряд конденсатора.
Объединяя формулы (3) – (5), получаем дифференциальное соотношение, в которое входит искомое произведение CR:
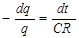 .
.
После интегрирования получаем
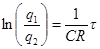 , (6)
, (6)
где q1 – начальный заряд конденсатора; q2 – конечный.
Подставляя CRиз (6) в (2), окончательно имеем
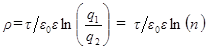 .
.
Дата добавления: 2016-07-27; просмотров: 9339;











