Примеры применения теоремы Гаусса к расчёту электростатических полей

Поле заряда q, равномерно распределённого по поверхности сферы радиусом R с поверхностной плотностью 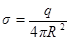выражается формулами:

если r > R, то 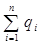= q и Е _r = .

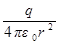если r < R, то 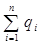= 0 и Е _r = 0.

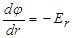Из связи между потенциалом и напряжённостью поля следует, что . Полагая j =0 при r®¥ , получим для потенциала поля вне сферы (r³R):

.

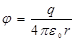Внутри сферы (r<R) потенциал всюду одинаков:

j = sR/e₀.

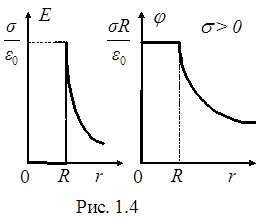
Графики зависимостей E _r и j от r приведены на рис. 1.4.

Поле заряда q, равномерно распределённого в вакууме по объёму шара радиусом R с объёмной плотностью 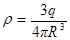выражается формулами:

если r>R, то 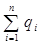= q и ;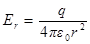

если r<R, то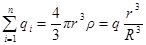

и .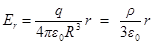

Из связи j и 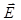следует, что для r>R ,

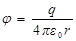для r<R j = j(R) - 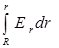и .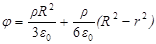

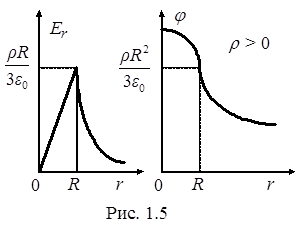
Графики зависимостей Е _r и j от r приведены на рис. 1.5.

Поле заряда, равномерно распределенного в вакууме по плоскости с поверхностной плотностью s.

Эта плоскость (х=0) является плоскостью симметрии поля, вектор напряжённости 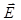которого направлен перпендикулярно плоскости от неё (если s>0) или к ней (если s < 0).

Для всех точек поля

.

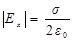Так как 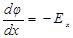, и полагая потенциал поля равным нулю в точках заряженной плоскости (х = 0), получим

.

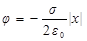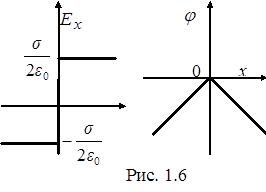
Графики зависимостей Е и j от x приведены на рис. 1.6.