Основные определения

В плоском криволинейном стержне так же, как в плоской раме, состоящей из прямолинейных стержней, возникает три внутренних усилия: N, Q и М. Процесс определения внутренних усилий в криволинейном стержне тот же, что и в раме. Особенность состоит в новом правиле знаков для изгибающего момента: изгибающий момент считается положительным, если он увеличивает кривизну стержня[15]. Правила знаков для продольной и поперечной сил те же, что и при их определении в плоских рамах.

При чистом изгибе в криволинейных стержнях возникают нормальные напряжения, которые вычисляются по формуле

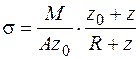, (4.39)

где 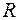– радиус кривизны оси стержня; 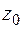– величина смещения нейтральной оси от главной центральной оси сечения в сторону центра кривизны (точка С на рис. 4.50); 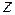– координата той точки, в которой мы ищем напряжения в главной центральной системе координат. Для того, чтобы формула (4.39) при определении напряжений правильно давала знак напряжений, ось 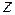следует направлять в сторону от центра кривизны. Формула (4.39) показывает, что нормальные напряжения в поперечном сечении криволинейного стержня распределяются не по линейному закону, как в прямолинейном стержне, а по гиперболическому. Эпюра нормальных напряжений в криволинейном стержне при чистом изгибе показана на рис. 4.50.

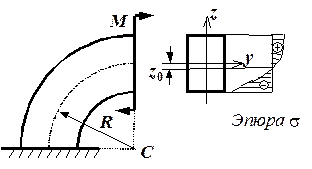Рис. 4.50. Распределение напряжений в сечении кривого бруса при чистом изгибе

Для определения величины 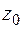существуют разные пути. Будем делить криволинейные стержни в зависимости от отношения 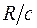(где с – расстояние от центра тяжести сечения до крайнего внутреннего волокна) на стержни большой ( 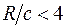), средней ( 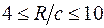) и малой кривизны ( 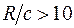). Для стержней большой кривизны при определении 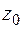рекомендуем использовать точные формулы для простых форм сечений (прямоугольник, круг), полученные в [2, § 46]. Если поперечное сечение имеет более сложную форму, то при определении величины 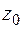для стержней большой и средней кривизны можно использовать либо приближенные формулы [2, § 46], либо таблицы, приведенные в [7, § 139]. Для стержней малой и средней кривизны допустимо использовать приближенную формулу

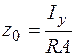. (4.40)

Если в сечении, кроме изгибающего момента, действует продольная сила, то в формулу (4.39) добавляется слагаемое 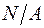. Касательные напряжения от поперечной силы в практических расчетах для криволинейных стержней обычно не учитывают.

Для определения перемещений точек оси криволинейных стержней большой кривизны используется метод Максвелла – Мора, согласно которому обобщенное перемещение 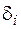находится по формуле [2]

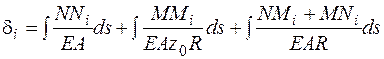, (4.41)

где N, M – продольная сила и изгибающий момент от заданной нагрузки, 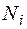, 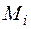– продольная сила и изгибающий момент, вызванные обобщенной силой, соответствующей искомому перемещению. Интегрирование ведется по длине дуги оси стержня ( 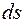– дифференциал дуги). Для криволинейных стержней малой и средней кривизны допустимо определять перемещения по формуле Максвелла – Мора для прямолинейных стержней, заменяя 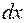на :

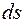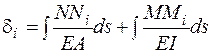. (4.42)

Видно, что формула (4.41) отличается от формулы Максвелла – Мора для прямолинейных стержней (4.42) знаменателем второго слагаемого ( 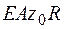вместо 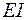) и наличием третьего слагаемого. Влияние поперечной силы на перемещения в обеих формулах не учитывается.