Теоретические основы процессов гравитационного обогащения
Основные закономерности процессов гравитационного обогащения начали разрабатываться в середине ХIХ века как русскими ( Г.Я.Дорошенко, С.Г.Войслов, В.А.Гуськов, Г.О.Чечотт, П.В.Лященко и др), так и зарубежными учеными (Риттингер, Стокс, Ален, Ричардс и др).
В основе теоретических исследований лежат закономерности движения в средах зерен различной плотности и крупности в свободных и стесненных условиях. Для обяснения этих закономерностей используются законы классической механики, гидромеханики, аэромеханики и гидравлики. 
Все тела в пустоте падают с одинаковой скоростью независимо от их размера, формы и плотности. В то время как в воде или в другой среде скорость падения тела 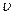 зависит от его диаметра d, формы, плотности
зависит от его диаметра d, формы, плотности 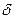 и плотности среды.
и плотности среды.
Минеральная частица, падающая в какой-либо среде, обладает гравитационной силой, зависящей от скорости ее движения. Чем больше скорость движения, тем больше эта сила. При этом падающая частица встречает сопротивление среды, поэтому скорость ее падения, например, в водной среде, значительно меньше скорости падения в пустоте.
 При большой скорости движения частица преодолевает динамическое сопротивление среды, характерное для турбулентного потока, при котором позади частицы при ее движении образуется пространство с повышенным давлением, что приводит к образованием вихрей позади частицы ( рис.71 а).
При большой скорости движения частица преодолевает динамическое сопротивление среды, характерное для турбулентного потока, при котором позади частицы при ее движении образуется пространство с повышенным давлением, что приводит к образованием вихрей позади частицы ( рис.71 а).
При медленном движении частицы небольших размеров испытывают сопротивление среды, обусловленное их вязкостью и вызываемое трением обтекаемых слоев жидкости. В этом случае наблюдается ламинарное движение ( рис. 71 б)

Рис.71. Характер обтекания жидкостью круглого тела при ламинарном ( а ) и турбулентном (б) движении жидкости
При этом следует также учитывать условия движения частицы. Свободное движение – это движение единичных зерен в неограниченной неподвижной среде, исключающей взаимное воздействие зерен друг на друга. Стесненное падение происходит или в ограниченном пространстве, соизмеримым с размерами зерна или в присутствии других зерен, когда частица испытывает влияние не только среды, но и окружающих частиц.
Скорость движения частиц в свободных условиях будет определяться силами сопротивления среды – динамического для крупных частиц без учета сил трения и сопротивления вязкости среды ( статического ) для мелких частиц.
Динамическое сопротивление, т.е. сопротивление сил инерции изучено Ньютоном, который
установил, что сопротивление среды пропорционально скорости падения частицы. Риттингер и Стокс, учитывая это сопротивление, вывели закон падения тел в среде, а П.В.Лященко внес в этот закон ряд дополнений и изменений..
Если падающая в спокойной среде минеральная частица имеет шарообразную форму диаметром d и плотностью 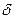 , то она находится под действием силы тяжести G1, направленной вниз, и динамической силы сопротивления среды Рd . Тогда масса этой частицы в среде по закону Архимеда будет равна
, то она находится под действием силы тяжести G1, направленной вниз, и динамической силы сопротивления среды Рd . Тогда масса этой частицы в среде по закону Архимеда будет равна
G = G1 – Q = 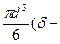 Δ) g, (72)
Δ) g, (72)
Откуда
G1 = 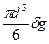 и Q =
и Q = 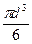 Δ g,
Δ g,
где Q – масса среды, вытесненная частицей;
G1 – сила тяжести частицы;
g - ускорение свободного падения;
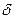 - плотность частицы;.
- плотность частицы;.
Δ - плотность среды.
Сила сопротивления среды для этой частицы
Рd = 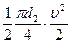 Δ, (73)
Δ, (73)
где 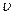 - скорость движения частицы.
- скорость движения частицы.
По этим уравнениям можно определить скорость движения частицы в каждый данный момент. Составим дифференциальное уравнение движения частицы. Так как вес ее есть произведение массы на ускорение свободного падения, то уравнение примет вид
m 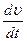 =
= 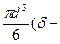 Δ)g -
Δ)g - 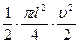 Δ,
Δ,
где m – масса частицы, 
dv/ dt – ускорение.
Если обе части уравнения разделить на массу m = 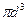 / 6, то получим
/ 6, то получим
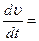
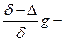
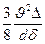 ,м/с2
,м/с2
Отсюда следует, что ускорение падающей частицы в среде равно разности двух ускорений; начального ускорения в среде go = [( 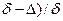 ] g и ускорения силы сопротивления среды g1 = 3/8
] g и ускорения силы сопротивления среды g1 = 3/8 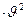 Δ/d
Δ/d 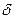 , зависящего от скорости
, зависящего от скорости 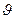 , плотности среды Δ, плотности частицы
, плотности среды Δ, плотности частицы 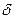 и ее диаметра d.
и ее диаметра d.
С увеличением скорости падения частицы будет увеличиваться и сила сопротивления среды Pd. При достижении частицей постоянной скорости падения это ускорение будет равно нулю, т.е. d 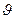 /dt =go – g1 = 0, при этом скорость падения будет называться конечной ( предельной) и наступает она очень быстро. Так для минеральных зерен шарообразной
/dt =go – g1 = 0, при этом скорость падения будет называться конечной ( предельной) и наступает она очень быстро. Так для минеральных зерен шарообразной  формы диаметром 1 мм конечная скорость падения достигается через 0,01 -0,1 доли секунды. Эту скорость можно определить из уравнения
формы диаметром 1 мм конечная скорость падения достигается через 0,01 -0,1 доли секунды. Эту скорость можно определить из уравнения
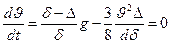
Отсюда
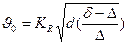 см/с (74)
см/с (74)
Это выражение называется формулой Риттингера и применяется для определения конечной скорости падения частиц любой формы крупностью от 1,5 до 15 мм. Из формулы следует, что конечная скорость падения частицы при прочих равных условиях будет тем больше, чем больше диаметр ее и плотность. При определении скорости падения частиц шарообразной формы коэффициент KR принимается равным 52,2, тогда формула (70) примет вид
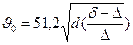 , см/с (75)
, см/с (75)
При падении в среде мелких частиц, скорость падения которых очень мала, динамическим сопротивлением среды можно пренебречь, а учитывать лишь сопротивление вязкости среды и наличие вокруг падающих частиц тонкого неподвижного слоя среды, создающее сопротивление падения частицы.
Величина сопротивления, испытываемого падающей частицей шарообразной формы небольшого диаметра, была определена английским физиком Стоксом и равна
PS = 3πμd 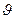 , (76)
, (76)
где μ – коэффициент вязкости жидкости, ( Н · с)/м2.
При температуре 20ºС вязкость воды равна 0,001 Па·с. С увеличением температуры на 1º вязкость уменьшается на 2%.
Учитывая сопротивление вязкости и пренебрегая динамическим сопротивлением, дифференциальное уравнение движения падающей шарообразной частицы будет
m 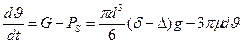
При достижении конечной скорости падения частицы ускорение будет равно нулю, т.е.

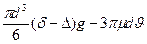 ,
,
Отсюда
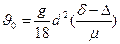 , см/с
, см/с
Обозначив 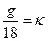 и приняв g = 9,18 см/с, получим
и приняв g = 9,18 см/с, получим
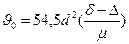 , см/с (77)
, см/с (77)
Эта формула стокса, которая применима для определения конечной скорости падения частиц размером от 0,12 до 0,012 мм.
Зерна промежуточной крупности определяется по эмпирической формуле Аллена
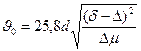 , см/с (78)
, см/с (78)
Эта формула применима для расчета конечных скоростей падения частиц крупностью от 0,085 до 0,15 мм.
Каждая из приведенных формул учитывает лишь один из видов сопротивления и применяется для сравнительно узкого класса крупности частиц.
Если d 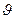
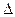 > 36μ , то Pd > PS , т.е. динамическое сопротивление больше силы сопротивления вязкости. В этом случае применяется формула Риттингера. При Pd < PS применяется формула Стокса. Этот вывод вытекает из соотношения двух сил сопротивления
> 36μ , то Pd > PS , т.е. динамическое сопротивление больше силы сопротивления вязкости. В этом случае применяется формула Риттингера. При Pd < PS применяется формула Стокса. Этот вывод вытекает из соотношения двух сил сопротивления
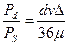 (78)
(78)
При равенстве этих сил dvΔ/36μ = 1 или dvΔ/μ = 36. Это отношение называется параметром или критерием Рейнольдса, обозначается Re и характеризует преобладание того или иного вида сопротивления. Если Re >36, то Pd > PS при Re< 36, Pd < PS .
Экспериментальные исследования показали, что формула Риттингера справедлива при
Re > 1000 и размере частиц более 2 мм, когда наблюдается турбулентный режим движения, а формула Стокса при Re < 1 и размере частиц не более 0,1 мм при ламинарном режиме движения частиц.
Между критерием Рейнольдса и сопротивлением, испытываемым частицей при падении в среде, существует зависимость, выведенная экспериментально Рейлеем и названная коэффициентом сопротивления 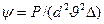 . Зависимость между критерием Рейнольдса Re и коэффициентом сопротивления
. Зависимость между критерием Рейнольдса Re и коэффициентом сопротивления 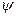 может быть представлена в виде диаграммы Рейлея ( рис.72), по которой можно судить о постепенном переходе от одного режима движения к другому.
может быть представлена в виде диаграммы Рейлея ( рис.72), по которой можно судить о постепенном переходе от одного режима движения к другому.

Рис.72. Диаграмма Рейлея
.В.Лященко, используя критерий Рейнольдса и коэффициент среды, предложил новый параметр, названный параметром Лященко.
Из формулы, определяющей критерий Рейнольдса, следует
v2d2 = 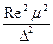 ,
,
а из формулы сопротивления среды v2d2 = 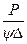
Тогда Re2μ/Δ= Р/ 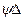 , откуда Re2 ψ = РΔ/μ2 , где Re2 ψ – параметр Лященко.
, откуда Re2 ψ = РΔ/μ2 , где Re2 ψ – параметр Лященко.
Расчет конечной скорости падения частиц по этому параметру производится следующим образом. Если частица падает в воде с постоянной конечной скоростью, то сила сопротивления среды уравновешивается силой тяжести частицы, т.е.
Р = G0 и Re2 ψ = 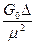 (79)
(79)
Определив по формуле (74) параметр Лященко, по диаграмме, представленной на рис. 73, находится значение параметра Рейнольдса. По формуле
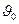 = Reμ/dΔ, см/с (80)
= Reμ/dΔ, см/с (80)
определяется конечная скорость падения частицы.

Рис. 73. Диаграмма зависимости параметра Лященко Re2ψ от числа Рейнольдса
Практически все минеральные частицы после дробления и измельчения имеют не шарообразную форму, а округлую, плоскую, продолговатую и др. Поэтому скорости падения частиц различной формы будут отличаться от скорости падения частиц, вычисленных по теоретическим формулам для шарообразных частиц. Установлено, что скорость падения частиц неправильной формы значительно меньше теоретической ,однако они подчиняются тем же законам, что и падение частиц шарообразной формы и оличаются лишь значением поправочного коэффициента, который определяется для любого минерала в зависимости от его диаметра, плотности, формы и шероховатости поверхности.
Например, для определения коэффициента в формуле Риттингера сначала определяется эквивалентный диаметр частицы, т.е диаметр частицы, которая имеет такой же объем, что и объем шара одинакового диаметра с частицей.
Коэффициент KR определяется по формуле (74)
KR = 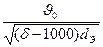 ,
,
Где dЭ – эквивалентный диаметр зерна.
Подобным образом экспериментально были определены коэффициенты КR для расчета скоростей падения минеральных частиц различной формы. Для частиц пластинчатой формы этот коэффициент равен 22,7, для продолговатой – 33,4, для угловатой – 35,8, для округлой – 42,2.
В настоящее время расчет конечных скоростей падения частиц осуществляется на компьютере.
При падении в среде частиц различной крупности и плотности крупные зерна легкого минерала будут падать с такой же скоростью, с какой падают мелкие зерна тяжелого минерала, т.е. эти зерна будут иметь одну и ту же конечную скорость падения. Минеральные частицы, имеющие различную крупность и плотность, но падающие всреде с одинаковой скоростью, называются равнопадающими.
Например, скорость падения частицы кварца, имеющей плотность 2650 кг/м3 и крупность 10 мм в воде будет равна
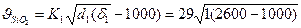 ≈ 37 см/с
≈ 37 см/с
С этой же скоростью будет падать частица галенита плотностью 7650 кг/м3, размер которой можно определить по формуле
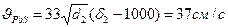 ,
,
Отсюда
d2 = 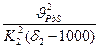 ≈ 0,2 см = 2 мм
≈ 0,2 см = 2 мм 
Следовательно, с одинаковой скоростью будут падать частицы кварца диаметром 10 мм и частицы галенита диаметром 2 мм. Таки частицы будут называться равнопадающими. Отношение диаметров равнопадающих легких и тяжелых частиц называется коэффициентом равнопадаемости е, т.е. е = 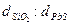 = 10 : 2 = 5
= 10 : 2 = 5
Коэффициент равнопадаемости для минеральных частиц различной крупностив общем виде определяется по формулам конечных скоростей падения.
По формуле Риттингера
е = 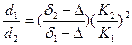
Незначительной разницей между К1 и К2 можно пренебречь, тогда коэффициент равнопадаемости будет равен
е1 = 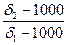 (81)
(81)
Таким образом, коэффициент равнопадаемости прямо пропорционален отношению диаметрам частиц и обратно пропорционален отношению плотностей минералов минус плотность среды.
Для минеральных зерен, конечная скорость которых подчиняется закону Стокса, коэффициент равнопадаемости будет
е2 = 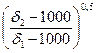 (82)
(82)
Для минеральных зерен промежуточной крупности в соответствии с формулой Алена коэффициент равнопадаемости определяется по формуле
е3 = 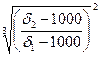 (83)
(83)
В зависимости от крупности частиц коэффициенты изменяются, например, для кварца и галенита они будут соответственно равны е1 ≈ 4 ; е2 ≈ 3,7 и е3 ≈ 2,4.
Рассмотрим процесс разделения рудного материала на равнопадающие зерна методов гидравлической классификации. Эта классификация проводится в гидравлических классификаторах, имеющих несколько камер. Получение в каждой из камер равнопадающих частиц обеспечивается скоростью восходящей струи воды по максимальной граничной частице легкого минерала. Крупность граничных частиц легкого и тяжелого минерала в каждой камере определяется с помощью коэффициентов равнопадаемости.
При классификации смеси частиц кварца и галенита крупностью минус 10 мм в соответствии с коэффициентом равнопадаемости в первый класс выпадут частицы, скорость падения которых может быть определена по формуле Риттингера. Используя значение коэффициента равнопадаемости, равного 4, размер частиц галенита, которые падают с той же скоростью, что и частицы кварца крупностью 10 мм, будет равен
е1 = d1/d2 ; или 4 = 10/d2 , откуда d2 = 2,5 мм
Во втором классе
е1 = d2 /d3 или 4 = 2,5 /d3 , d3 = 0,62 мм.
Для третьего класса крупность разделяемых частиц при падении соответствует формуле Алена с коэффициентом равнопадаемости 3,7. Тогда е3 = d3 / d4 ; 3,7 = 0,62 / d4 , откуда d4 = 0, 16 мм.
Для мелких частиц применяется формула Стокса с коэффициентом равнопадаемости 2,4. Тогда е2 = d4 /d5 ; 2,4 = 0,16/d5 , откуда d5 = 0,07 мм и т.д.
Таким образом, для классификации по равнопадаемости должны быть приняты скорости восходящей струи воды в каждой камере, равные скорости падения крупного зерна легкого минерала. В первой камере для частицы кварца крупностью 10 мм эта скорость должна быть равна
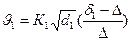 ≈ 29
≈ 29 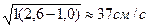
Во второй камере скорость восходящей струи воды должна быть равна скорости падения частиц кварца крупностью 2,5 мм и т.д.
В результате гидравлической классификации в камерах выделяются равнопадающие частицы кварца и галенита следующей крупности:
Дата добавления: 2020-11-18; просмотров: 1124;











