Основные формулы и законы
· Первый постулат Бора (постулат стационарных состояний):
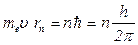 (
( 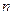 = 1, 2, 3,…),
= 1, 2, 3,…),
где 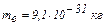 – масса электрона;
– масса электрона; 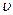 – скорость электрона на
– скорость электрона на 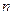 -й орбите, радиус которой равен
-й орбите, радиус которой равен 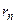 ;
;
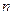 – номер стационарного состояния;
– номер стационарного состояния; 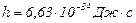 – постоянная Планка.
– постоянная Планка.
· Второй постулат Бора (правило частот)

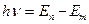 ,
,
где 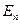 ,
, 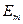 – энергии стационарных состояний атома соответственно до и после излучения (поглощения);
– энергии стационарных состояний атома соответственно до и после излучения (поглощения); 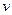 – частота излученного (поглощенного) кванта энергии.
– частота излученного (поглощенного) кванта энергии.
· Обобщенная формула Бальмера, описывающая серии линий в спектре атома водорода:
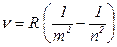 ,
,
где 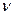 – частота спектральных линий в спектре атома водорода;
– частота спектральных линий в спектре атома водорода;
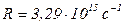 - постоянная Ридберга;
- постоянная Ридберга;  – целое число, определяет серию линий в спектре атома водорода:
– целое число, определяет серию линий в спектре атома водорода:  = 1 – серия Лаймана (расположена в ультрафиолетовой части);
= 1 – серия Лаймана (расположена в ультрафиолетовой части);
 = 2 – серия Бальмера (расположена в видимой части спектра);
= 2 – серия Бальмера (расположена в видимой части спектра);
 = 3 – серия Пашена;
= 3 – серия Пашена;
 = 4 – серия Брэкета;
= 4 – серия Брэкета;
 = 5 – серия Пфунда; расположены в инфракрасной
= 5 – серия Пфунда; расположены в инфракрасной
 = 6 – серия Хэмфри. части спектра
= 6 – серия Хэмфри. части спектра
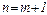 – определяет отдельные линии соответствующей серии
– определяет отдельные линии соответствующей серии  .
.
· Радиус 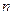 -й орбиты электрона в атоме водорода
-й орбиты электрона в атоме водорода
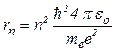 ,
,
где 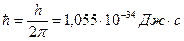 – постоянная Планка;
– постоянная Планка;
 – электрическая постоянная;
– электрическая постоянная; 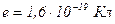 – заряд электрона;
– заряд электрона; 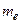 – масса электрона.
– масса электрона.
· Энергия 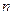 -го стационарного состояния атома водорода:
-го стационарного состояния атома водорода:
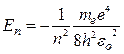 ,
,
где 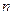 – номер стационарной орбиты.
– номер стационарной орбиты.
· Энергия электрона в атоме водорода
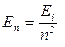 ,
,
где 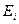 – энергия ионизации атома водорода.
– энергия ионизации атома водорода.
· Потенциал ионизации:
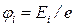 .
.
· Потенциал возбуждения:
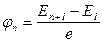 .
.
· Длина волны де Бройля
 ,
,
где 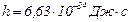 – постоянная Планка;
– постоянная Планка; 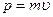 – импульс частицы (
– импульс частицы (  – масса частицы;
– масса частицы; 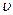 – её скорость).
– её скорость).
· Связь импульса частицы 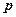 с ее кинетической энергией
с ее кинетической энергией 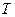 :
:
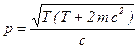 ,
,
где  – масса покоя частицы. При малых скоростях
– масса покоя частицы. При малых скоростях  .
.
Соотношение неопределенностей Гейзенберга: 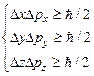
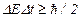 ,
,
где 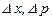 ,
, 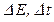 – соответственно неопределенности координаты, импульса, энергии и времени,
– соответственно неопределенности координаты, импульса, энергии и времени,  .
.
· Нестационарное уравнение Шредингера:
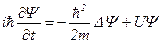 .
.
· Уравнение Шредингера для стационарных состояний:
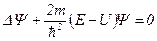 ,
,
где 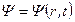 – волновая функция микрочастицы;
– волновая функция микрочастицы; 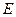 – полная энергия микрочастицы;
– полная энергия микрочастицы; 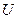 =
=  – потенциальная энергия частицы;
– потенциальная энергия частицы; 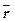 – пространственная координата (
– пространственная координата ( 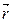 =
= 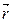
 ); t – время, ∆=
); t – время, ∆= 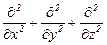 – оператор Лапласа (записан в декартовых координатах);
– оператор Лапласа (записан в декартовых координатах);  – масса микрочастицы;
– масса микрочастицы; 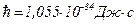 – постоянная Планка;
– постоянная Планка;  =
= 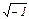 – мнимая единица.
– мнимая единица.
· Одномерное уравнение Шредингера для стационарных состояний:
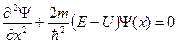 .
.
· Условие нормировки волновой функции:
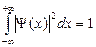
 .
.
· Плотность вероятности:
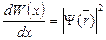

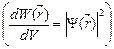 ,
,
где 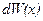 – вероятность того, что частица может быть обнаружена вблизи точки с координатой
– вероятность того, что частица может быть обнаружена вблизи точки с координатой 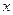 на участке
на участке  .
.
· Вероятность обнаружения частицы в интервале от 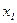 до
до 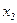 :
:
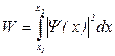 .
.
· Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика шириной 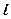 (0 ≥
(0 ≥ 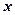 ≥
≥ 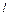 ):
):

 (собственная нормированная волновая функция),
(собственная нормированная волновая функция),
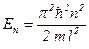 (собственное значение энергии),
(собственное значение энергии),
где 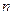 – главное квантовое число (
– главное квантовое число ( 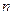 = 1, 2, 3,…). В области 0≥
= 1, 2, 3,…). В области 0≥ 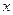 ≥
≥ 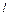
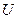 = ∞ и
= ∞ и 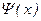 = 0.
= 0.
Дата добавления: 2020-10-25; просмотров: 461;











