Примеры решения задач
Задача 1. Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи силой I = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию В в точке А, отстоящей от одного проводника на расстоянии r1=5 см и от другого – на расстоянии r2 = 12 см.
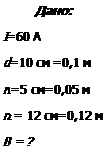
 Решение:
Решение:
Для нахождения магнитной индукции В в точке А определим направления векторов индукции  и
и 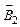 полей (по правилу «правого винта»), создаваемых каждым проводником в отдельности, и сложим их геометрически, т.е.
полей (по правилу «правого винта»), создаваемых каждым проводником в отдельности, и сложим их геометрически, т.е. 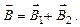
 Абсолютное значение индукции найдем по теореме косинусов:
Абсолютное значение индукции найдем по теореме косинусов:

Учтя, что 
Получаем: 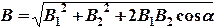 (1)
(1)
Значения индукции В1 и В2 выражаются соответственно через силу тока I и расстояния r1 и r2 от провода до точки, индукцию в которой мы вычисляем:
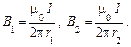
Подставив В1 и В2 в формулу (1) и вынеся 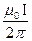 за знак корня, получим
за знак корня, получим
 (2)
(2)
Проверяем наименования: 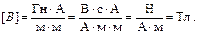
Вычислим угол 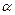 . Заметим, что
. Заметим, что 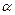 =ÐDAC. Поэтому по теореме косинусов запишем d 2= r12 + r22 – 2r1r2cos
=ÐDAC. Поэтому по теореме косинусов запишем d 2= r12 + r22 – 2r1r2cos 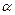 , где d – расстояние между проводами. Отсюда
, где d – расстояние между проводами. Отсюда 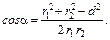
Подставив данные, вычислим значение косинуса:
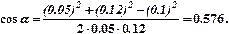
Подставив в формулу (2) значения 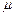 0, I, r1, r2 и cos
0, I, r1, r2 и cos 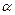 , найдем
, найдем

Ответ: 
Задача 2. По двум параллельным прямым проводникам длиной l = 2м каждый, находящимся в вакууме на расстоянии r = 10 см друг от друга, в противоположных направлениях текут токи I1 = 50A и I2 = 100A. Определить силу взаимодействия проводников между собой.

Решение
Согласно закону Ампера, на каждый элемент длины проводника dl с током I2 действует в магнитном поле, создаваемом током I1, сила
dF1 = I2B1dl (1)
(eё направление определено по правилу левой руки и указано на рисунке).
Аналогичные рассуждения (ток I1 находится в магнитном поле, создаваемом током I2) приводят к выражению
dF2 = I1B2dl . (2)
Модули магнитных индукций  определяются соотношениями:
определяются соотношениями: 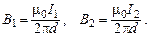

|
Подставив эти выражения в (1) и (2), получим, что по модулю
 (3)
(3)
(направления сил указаны на рисунке).
Проинтегрировав выражение (3), найдем искомую силу взаимодействия: 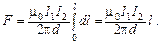
Проверим наименования:
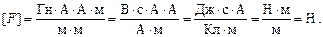
Вычисляя, получаем
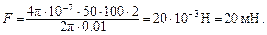
Ответ: 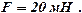
Задача 3. В однородном магнитном поле с индукцией В=0,1Тл равномерно вращается рамка, содержащая N=1000 витков, с частотой n=10с-1. Площадь S рамки равна 150 см2. Определить мгновенное значение ЭДС индукции ei, соответствующее углу поворота рамки на 300.
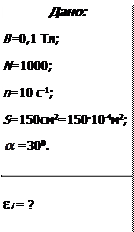 Решение
Решение
Мгновенное значение ЭДС индукции ei определяется основным уравнением электромагнитной индукции Фарадея-Максвелла
ei = – dY/dt , (1)
где Y=NФ – потокосцепление, N – число витков, пронизываемых магнитным потоком Ф.
Подставив выражение для потокосцепления Y в формулу(1), получим ei 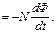 (2)
(2)
При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, изменяется по закону
Ф = BS cos 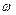 t , (3)
t , (3)
где В – магнитная индукция; S – площадь рамки; 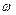 – круговая частота.
– круговая частота.
Решив совместно уравнения (1)–(3), найдем мгновенное значение ЭДС индукции
ei = 2  NBS sin 300.
NBS sin 300.
Проверим наименования:
ei 
Произведя вычисления, получим
ei = 2  ·10·1000·0,1·150·10-4·sin 300 = 47,1 B.
·10·1000·0,1·150·10-4·sin 300 = 47,1 B.
Задача 4. Электрон, пройдя ускоряющую разность потенциалов U=400 В, попал в однородное магнитное поле с индукцией В=1,5 мТл. Определить: 1) радиус R кривизны траектории; 2) частоту  вращения электрона в магнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.
вращения электрона в магнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.
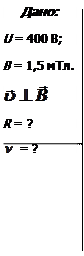 Решение
Решение
1. На движущийся в магнитном поле электрон действует сила Лоренца:
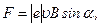
(Действием силы тяжести можно пренебречь.)
Вектор силы Лоренца перпендикулярен вектору скорости и, следовательно, по второму закону Ньютона сила Лоренца является центростремительной силой, т.е. 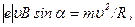 (1)
(1)
где e, u, m – заряд, скорость, масса электрона; В – индукция магнитного поля; R – радиус кривизны траектории; 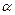 – угол между направлениями вектора скорости
– угол между направлениями вектора скорости 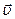 и индукции
и индукции  (в нашем случае
(в нашем случае 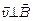
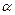 = 900, sin
= 900, sin 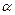 = 1).
= 1).
Из формулы (1) найдем
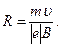 (2)
(2)
Электрон, пройдя ускоряющую разность потенциалов U, получает энергию 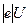 ,которая переходитв кинетическую энергию
,которая переходитв кинетическую энергию  , т.е.
, т.е. 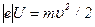 . Отсюда
. Отсюда  .
.
Подставив это выражение в формулу (2), получим выражение для радиуса кривизны:
 (3)
(3)
Подставляем числа в выражение (3):
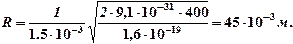
Проверим наименования:

2. Для определения частоты вращения воспользуемся формулой, связывающей частоту со скоростью и радиусом кривизны траектории,  Подставив R из выражения (2) в эту формулу, получим
Подставив R из выражения (2) в эту формулу, получим  Производим вычисления:
Производим вычисления:
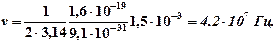
Проверим наименования
 .
.
Ответ: 

Задача 5. Электрон, имея скорость u=2 Мм/с, влетел в однородное магнитное поле с индукцией В=30 мТл под углом 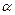 =300 к направлению линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон.
=300 к направлению линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон.
 Решение
Решение
Известно, что на заряженную частицу, влетевшую в магнитное поле, действует сила Лоренца, перпендикулярная векторам магнитной индукции  и скорости
и скорости 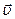 частицы:
частицы:
F = quB sin 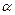 , (1)
, (1)
где q – заряд частицы. В случае, если частицей является электрон, формулу (1) можно записать в виде
F=|e|uB sin 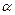 .
.

|
Так как вектор силы Лоренца перпендикулярен вектору скорости, то модуль скорости не будет изменяться под действием этой силы. Но при постоянной скорости, как это следует из формулы (1), останется постоянным и значение силы Лоренца. Из механики известно, что постоянная сила, перпендикулярная скорости, вызывает движение по окружности. Следовательно, электрон, влетевший в магнитное поле, будет двигаться по окружности в плоскости, перпендикулярной линиям индукции, со скоростью, равной поперечной составляющей uz скорости (рис.); одновременно он будет двигаться и вдоль поля со скоростью ux: uz=u sin 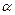 , ux = u cos
, ux = u cos 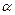 . В результате одновременного участия в движениях по окружности и по прямой электрон будет двигаться по винтовой линии. Радиус окружности, по которой движется электрон, найдем следующим образом.
. В результате одновременного участия в движениях по окружности и по прямой электрон будет двигаться по винтовой линии. Радиус окружности, по которой движется электрон, найдем следующим образом.
Сила Лоренца F сообщает электрону нормальное ускорение аn. По второму закону Ньютона F=mаn, где F=|e|uzB и 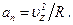 Тогда
Тогда 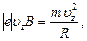 откуда после сокращения на uz находим радиус винтовой линии:
откуда после сокращения на uz находим радиус винтовой линии:
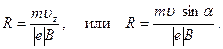
Проверим наименования

Подставив значения величин m, u, e, B и 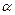 и произведя вычисления, получим R = 0,19 мм.
и произведя вычисления, получим R = 0,19 мм.
Шаг винтовой линии равен пути, пройденному электроном вдоль поля со скоростью ux за время, которое понадобиться электрону для того, чтобы совершить один оборот, h=uxT, где T=2 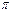 R/uz, или h=2
R/uz, или h=2 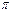 Ru cos
Ru cos 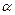 /(u sin
/(u sin 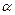 )=2
)=2 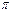 R ctg
R ctg 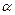 .
.
Проверим наименования

Подставив в эту формулу значения величин 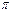 , R и
, R и 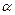 и вычислив, получим
и вычислив, получим
h = 2,06 мм.
Ответ: h = 2,06 мм.
Дата добавления: 2020-10-25; просмотров: 627;











