Электромагнетизм. Основные формулы
• Сила взаимодействия между двумя прямолинейными параллельными бесконечно длинными проводниками с токами 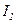 и
и  , приходящаяся на единицу длины
, приходящаяся на единицу длины
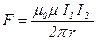 ,
,
где  – расстояние между проводниками,
– расстояние между проводниками,  – магнитная постоянная,
– магнитная постоянная,  – магнитная проницаемость изотропной среды (для вакуума
– магнитная проницаемость изотропной среды (для вакуума  ).
).
• Связь магнитной индукции  с напряженностью
с напряженностью  магнитного поля
магнитного поля

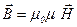 .
.
• Принцип суперпозиции магнитных полей

 ,
,  ,
,
где 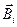 (
( 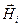 ) – магнитная индукция (напряжённость), создаваемая каждым током или движущимся зарядом в отдельности.
) – магнитная индукция (напряжённость), создаваемая каждым током или движущимся зарядом в отдельности.
• Магнитная индукция поля, создаваемая бесконечно длинным прямолинейным проводником с током,
 ,
,
где  – расстояние от проводника с током до точки, в которой определяется магнитная индукция.
– расстояние от проводника с током до точки, в которой определяется магнитная индукция.
• Магнитная индукция поля, создаваемого прямолинейным проводником с током конечной длины

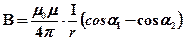 ,
,
где 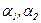 – углы между элементом тока и радиус-вектором, проведенным из рассматриваемой точки к концам проводника (рис).
– углы между элементом тока и радиус-вектором, проведенным из рассматриваемой точки к концам проводника (рис).
• Магнитная индукция поля в центре кругового проводника с током
 ,
,
где 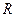 – радиус кругового витка.
– радиус кругового витка.
• Магнитная индукция поля на оси кругового проводника с током
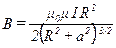 ,
,
где 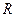 – радиус кругового витка,
– радиус кругового витка, 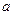 – расстояние от центра витка до точки, в которой определяется магнитная индукция.
– расстояние от центра витка до точки, в которой определяется магнитная индукция.
• Магнитная индукция поля внутри тороида
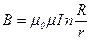 ,
,
где  – число витков на единицу длины,
– число витков на единицу длины, 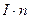 – число ампер-витков,
– число ампер-витков, 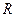 – радиус тороида,
– радиус тороида,  – радиус витка.
– радиус витка.
• Магнитная индукция поля бесконечно длинного соленоида и внутри тороида, радиус которого значительно больше радиуса витка,
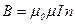 .
.
• Магнитная индукция поля на оси соленоида конечной длины
 ,
, 
где 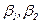 – углы между осью катушки и радиус-вектором, проведенным из данной точки к концам катушки.
– углы между осью катушки и радиус-вектором, проведенным из данной точки к концам катушки.
• Сила Ампера, действующая на элемент 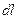 проводника с током
проводника с током 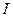 в магнитном поле,
в магнитном поле,
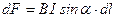 ,
, 
где 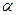 – угол между направлениями тока и магнитной индукции поля.
– угол между направлениями тока и магнитной индукции поля.
• Магнитный момент контура с током


где  – площадь контура,
– площадь контура, 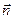 – единичный вектор нормали (положительный) к плоскости контура.
– единичный вектор нормали (положительный) к плоскости контура.
• Вращающий момент сил, действующий на контур с током, помещенный в однородное магнитное поле,
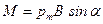 ,
,
где 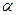 – угол между направлением нормали к плоскости контура и магнитной индукцией поля.
– угол между направлением нормали к плоскости контура и магнитной индукцией поля.
• Магнитный поток через площадку 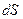
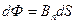 ,
,
где 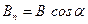 ,
, 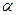 – угол между направлениями вектора магнитной индукции и нормалью к площадке
– угол между направлениями вектора магнитной индукции и нормалью к площадке 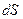 .
.
• Магнитный поток неоднородного поля через произвольную поверхность.
 ,
,
где интегрирование ведется по всей поверхности.
• Магнитный поток однородного поля через плоскую поверхность площадью 
 .
.
• Работа перемещения проводника с током в магнитном поле
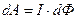 ,
,
где 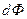 – поток магнитной индукции, пересеченный проводником при его движении.
– поток магнитной индукции, пересеченный проводником при его движении.
• Работа перемещения контура с током в магнитном поле
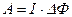 ,
,
где 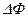 – изменение магнитного потока через поверхность, ограниченную контуром при его движении.
– изменение магнитного потока через поверхность, ограниченную контуром при его движении.
• Сила Лоренца, действующая на движущуюся заряженную частицу в магнитном поле,
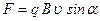 ,
,
где 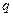 – заряд частицы,
– заряд частицы,  – скорость частицы,
– скорость частицы, 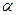 – угол между направлениями скорости частицы и магнитной индукции поля.
– угол между направлениями скорости частицы и магнитной индукции поля.
• Радиус окружности и период вращения частицы, влетевшей в магнитное поле под углом 90º к силовым линиям индукции,
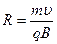 ,
, 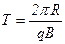 ,
, 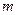 – масса частицы,
– масса частицы, 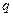 - заряд частицы.
- заряд частицы.
• Шаг винтовой траектории, по которой движется заряженная частица, влетевшая в магнитное поле под углом  к силовым линиям магнитного поля
к силовым линиям магнитного поля
 .
.
• ЭДС индукции, возникающая в контуре при изменении магнитного потока 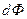 (закон Фараденя)
(закон Фараденя)

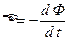 , или
, или  ,
,
где 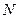 – общее число витков в контуре.
– общее число витков в контуре.
• Разность потенциалов на концах проводника, движущегося в магнитном поле,
 ,
,
где  – скорость движения проводника,
– скорость движения проводника, 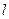 – длина проводника,
– длина проводника, 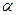 – угол между направлениями скорости движения проводника и магнитной индукцией поля.
– угол между направлениями скорости движения проводника и магнитной индукцией поля.
• ЭДС индукции, возникающая в рамке, содержащей 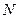 витков площадью
витков площадью  , при вращении рамки с угловой скоростью
, при вращении рамки с угловой скоростью 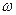 в однородном магнитном поле
в однородном магнитном поле
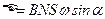 .
.
• Заряд, протекающий в контуре при изменении потока, пронизывающего поверхность, ограниченную контуром
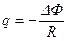 .
.
• ЭДС самоиндукции
 ,
,
где  – индуктивность контура.
– индуктивность контура.
• Индуктивность соленоида
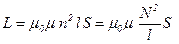 ,
,
где  – площадь поперечного сечения соленоида,
– площадь поперечного сечения соленоида, 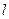 – длина соленоида,
– длина соленоида, 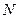 – полное число витков.
– полное число витков.
• Энергия магнитного поля контура с током
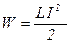 .
.
• Объемная плотность энергии магнитного поля

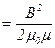 .
.
Дата добавления: 2020-10-25; просмотров: 474;











