Контрольные задания

5.1. При изотермическом расширении 2 г азота ( 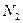) при температуре 280 К объём увеличился в два раза. Определите совершённую газом работу, изменение внутренней энергии и количество теплоты, полученное газом.

5.2. Азот ( 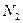) массой 0,1 кг изобарно нагрет от температуры 200 К до температуры 400 К. Определите работу, совершённую газом, полученную им теплоту и изменение внутренней энергии.

5.3. Водород ( 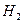) массой 6,5 г при температуре 300 К и постоянном давлении расширяется вдвое за счет притока тепла извне. Определите работу расширения, изменение внутренней энергии газа и количество теплоты, полученное газом.

5.4. 2 кмоля углекислого газа ( 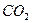) нагреваются при постоянном давлении на 50 К. Найдите изменение его внутренней энергии, работу расширения и количество теплоты, полученное газом.

5.5. При адиабатном расширении двух моль кислорода ( 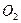), находящегося при нормальных условиях, объём увеличился в 3 раза. Определите изменение внутренней энергии газа и работу расширения газа.

5.6. Азот ( 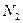), находившийся при температуре 400 К, подвергли адиабатному расширению, в результате которого его объем увеличился в 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определите массу азота.

5.7. Газ расширяется адиабатно и при этом его объём увеличивается вдвое, а температура падает в 1,32 раза. Найдите число степеней свободы этого газа.

5.8. Два моля двухатомного идеального газа нагревают при постоянном объеме до температуры 289 К. Определите количество теплоты, которое необходимо сообщить газу, чтобы увеличить его давление в 3 раза.

5.9. Работа расширения некоторого двухатомного идеального газа составляет 2 кДж. Определите количество подведенной к газу теплоты, если процесс протекал изобарно.

5.10. Определите количество теплоты, которое надо сообщить кислороду ( 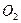) объёмом 50 л при изохорном нагревании, чтобы давление повысилось на 0,5 МПа.

Электростатика

Основные формулы

· Закон Кулона:

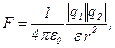
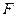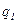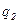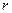где – модуль силы взаимодействия двух точечных зарядов и ; – расстояние между зарядами; 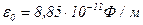- электрическая постоянная; 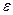-диэлектрическая проницаемость среды, в которой находятся заряды (для вакуума ).

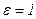· Напряженность и потенциал электростатического поля:

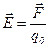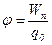, , или ,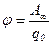

где 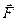– сила, действующая на точечный положительный заряд 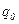, помещенный в данную точку поля; 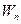– потенциальная энергия заряда 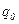; – работа по перемещению заряда 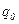из данной точки поля в бесконечность.

· Напряженность и потенциал электростатического поля, создаваемого точечным зарядом 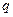на расстоянии 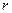от него

; .

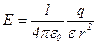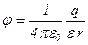· Поток вектора напряженности через площадку :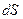

,

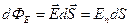где 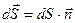– вектор, модуль которого равен 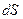, а направление совпадает с нормалью 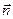к площадке; 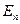– составляющая вектора 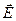по направлению нормали 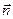к площадке.

· Поток вектора напряженности через произвольную поверхность :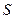

.

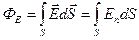· Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции (наложения) электростатических полей):

; ,

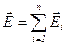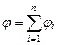где 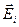, 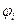– соответственно напряженность и потенциал поля, создаваемого зарядом 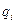, 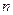– число зарядов, создающих поле.

· Связь между напряженностью и потенциалом электростатического поля:

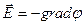, или ,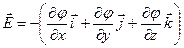

где 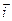, , 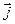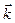– единичные векторы координатных осей.

· В случае поля, обладающего центральной или осевой симметрией:

.

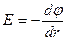· Для однородного поля (поля плоского конденсатора):

,

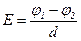где 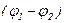– разность потенциалов между пластинами конденсатора, 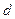– расстояние между ними.

· Электрический момент диполя (дипольный момент):

,

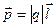где 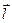– плечо диполя (векторная величина, направленная от отрицательного заряда к положительному).

· Линейная, поверхностная и объемная плотность зарядов, т.е. заряд, приходящийся соответственно на единицу длины, площади и объема:

; ; .

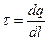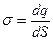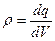· Теорема Гаусса для электростатического поля в вакууме:

,

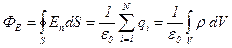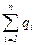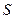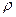где – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности ; – число зарядов; – объемная плотность зарядов.

· Напряженность поля, создаваемая равномерно заряженной бесконечной плоскостью:

.

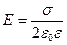· Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом 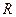с зарядом 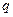на расстоянии 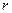от центра сферы:

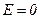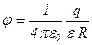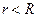; при (внутри сферы);

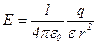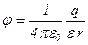; при 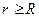(вне сферы).

· Напряженность поля, создаваемого равномерно заряженной бесконечной цилиндрической поверхностью радиусом 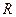на расстоянии 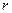от оси цилиндра:

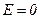при 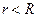(внутри цилиндра);

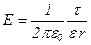при 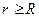(вне цилиндра).

· Работа, совершаемая силами электростатического поля при перемещении заряда 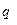из точки 1(потенциал 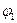) в точку 2 (потенциал ):

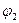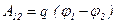, или ,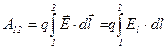

где 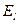– проекция вектора 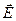на направление элементарного перемещения .

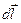· Вектор поляризации диэлектрика:

,

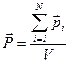где 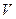– объем диэлектрика; 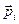– дипольный момент 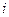-й молекулы, – число молекул.

· Связь между вектором поляризации и напряженностью электростатического поля в той же точке внутри диэлектрика:

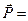æ _,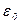

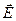где æ – диэлектрическая восприимчивость вещества.

· Связь диэлектрической проницаемости 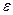с диэлектрической восприимчивостью æ:

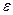= 1 + æ.

· Связь между напряженностью 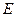поля в диэлектрике и напряженностью 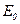внешнего поля:

.

· Связь между векторами электрического смещения и напряженности электростатического поля:

.

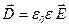· Связь между векторам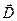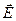и , и :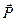

.

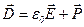· Теорема Гаусса для электростатического поля в диэлектрике:

,

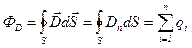где 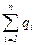– алгебраическая сумма заключенных внутри замкнутой поверхности 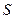свободных электрических зарядов; 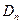– составляющая вектора 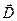по направлению нормали 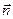к площадке ; 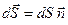– вектор, модуль которого равен 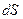, а направление совпадает с нормалью 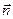к площадке. Интегрирование ведется по всей поверхности.

· Электроемкость уединенного проводника и конденсатора:

, ,

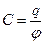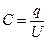где 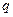– заряд, сообщенный проводнику; 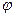– потенциал проводника;
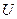– разность потенциалов между пластинами конденсатора.

· Электроемкость плоского конденсатора:

,

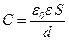где 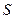– площадь пластины конденсатора; 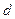– расстояние между пластинами.

· Электроемкость батареи конденсаторов: при последовательном (а) и параллельном (б) соединениях:

а) 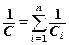, б) ,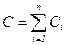

где 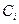– электроемкость 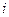-го конденсатора; 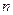– число конденсаторов.

· Энергия уединенного заряженного проводника:

.

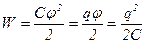· Потенциальная энергия системы точечных зарядов:

,

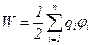где 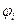– потенциал, создаваемый в той точке, где находится заряд 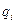, всеми зарядами, кроме 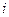-го, 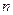- число зарядов.

· Энергия заряженного конденсатора:

,

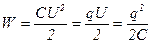где 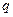– заряд конденсатора; 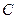– его электроёмкость; 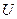– разность потенциалов между обкладками.

· Сила притяжения между двумя разноименно заряженными обкладками плоского конденсатора:

.

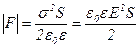· Энергия электростатического поля плоского конденсатора:

,

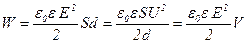где 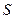– площадь одной пластины; 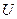– разность потенциалов между пластинами; 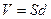– объем области между пластинами конденсатора.

· Объемная плотность энергии электростатического поля:

,

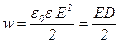где 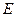– напряжённость поля, 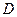– электрическое смещение.