Примеры решения задач. Какова сила натяжения шнура во время движения?
Задача 1. На шнуре, перекинутом через неподвижный блок, подвешены грузы массами 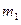 и
и 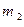 (
( 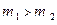 ). Считаем нить и блок невесомыми и пренебрегаем трением в блоке. С каким ускорением движутся грузы? Какова сила натяжения шнура во время движения?
). Считаем нить и блок невесомыми и пренебрегаем трением в блоке. С каким ускорением движутся грузы? Какова сила натяжения шнура во время движения?
Дано: Решение:
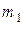 , , 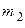 ; ( ; ( 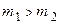 ). ). |
 Делаем рисунок, расставляем силы, действующие на каждое тело: Делаем рисунок, расставляем силы, действующие на каждое тело: 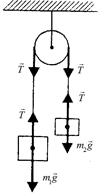 Рис.2.1 Рис.2.1 |
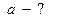 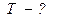 |
Записываем второй закон Ньютона для каждого тела в векторной форме:
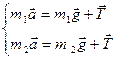
Поскольку 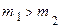 , считаем, что тело массой
, считаем, что тело массой 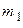 движется вниз, а тело массой
движется вниз, а тело массой 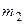 - вверх. Ось
- вверх. Ось 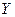 совпадает с направлением ускорения. Записываем второй закон Ньютона для каждого тела в проекции на направление оси
совпадает с направлением ускорения. Записываем второй закон Ньютона для каждого тела в проекции на направление оси 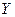 :
:
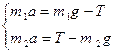
Складывая почленно эти уравнения, получаем:
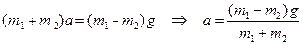 .
.
Подставляя это выражение в одно из уравнений системы, получаем  выражение для силы натяжения:
выражение для силы натяжения:
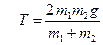 .
.
Задача 2. В установке (см. рис.2.2) угол наклонной плоскости с горизонтом 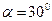 , массы тел
, массы тел 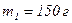 и
и 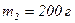 . Считая нить и блок невесомыми, определите ускорение, с которым движутся тела, и силу натяжения нити, если тело
. Считая нить и блок невесомыми, определите ускорение, с которым движутся тела, и силу натяжения нити, если тело 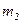 опускается. Коэффициент трения тела
опускается. Коэффициент трения тела 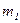 о плоскость равен 0,1.
о плоскость равен 0,1.
Дано: Решение:
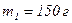 ; ; 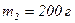 ; ; 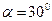 ; ; 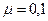 . . |
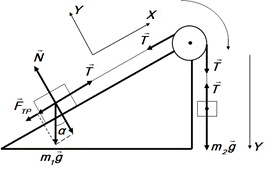
Рис.2.2 |
||
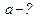 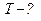 |
|||
Записываем второй закон Ньютона для каждого тела в векторной форме: 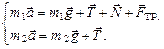 |
Для каждого тела устанавливаем оси координат и записываем второй закон Ньютона для каждого тела в проекциях на направления 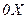 и
и 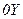 :
:
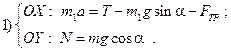
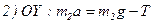 .
.
Учитывая, что 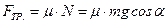 , получаем систему:
, получаем систему:
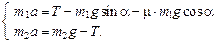
Складываем почленно эти уравнения:
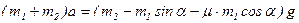 .
.
Отсюда получаем выражение для ускорения:
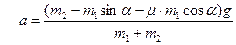 .
.
Подставляем числа:
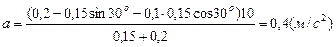 .
.
Из уравнения 2) выражаем силу натяжения: 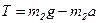 .
.
Подставляем числа: 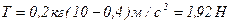 .
.
Ответ: 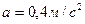 ;
; 
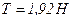 .
.
Задача 3. Движущееся тело массой 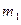 ударяется о неподвижное тело массой
ударяется о неподвижное тело массой 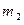 . Считая удар упругим и центральным, определите, какую часть своей первоначальной кинетической энергии первое тело передает второму при ударе. Задачу решите сначала в общем виде, а затем рассмотрите случаи: 1)
. Считая удар упругим и центральным, определите, какую часть своей первоначальной кинетической энергии первое тело передает второму при ударе. Задачу решите сначала в общем виде, а затем рассмотрите случаи: 1) 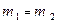 ; 2)
; 2) 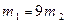 .
.
Дано: 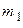 , , 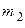 , , 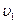 , , 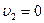 ; 1) ; 1) 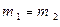 ; 2) ; 2) 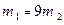 . . |
Решение: Пусть скорость первого тела до удара 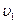 . Скорость второго тела до удара . Скорость второго тела до удара 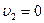 . Кинетическая энергия первого тела до удара . Кинетическая энергия первого тела до удара 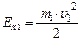 . Предположим, что скорость второго тела после удара равна . Предположим, что скорость второго тела после удара равна 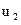 . Тогда кинетическая энергия второго тела после удара . Тогда кинетическая энергия второго тела после удара 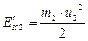 , а отношение энергий , а отношение энергий |
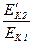 - ? - ? |
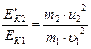 . (1)
. (1)
Для определения скорости второго тела после удара запишем закон сохранения импульса в проекции на направление движения и закон сохранения механической энергии, полагая, что система тел замкнута и в ней действуют только консервативные силы.
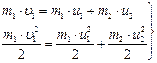 (2)
(2)
Преобразуем систему (2) к виду
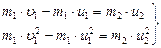 (3)
(3)
Разделив одно на другое выражения системы (3), получим 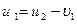 , а после подстановки скорости
, а после подстановки скорости 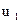 в первую формулу системы (3) получим
в первую формулу системы (3) получим
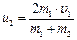 . (4)
. (4)
Отношение энергий (1) приобретает вид
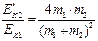 .
.
1) Если 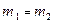 , то
, то 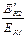 =1. При равенстве масс первое тело полностью отдает энергию второму, т.е. первое тело остановится, а второе начнет двигаться со скоростью первого тела.
=1. При равенстве масс первое тело полностью отдает энергию второму, т.е. первое тело остановится, а второе начнет двигаться со скоростью первого тела.
2) Если 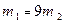 , то
, то 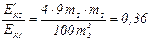 .
.
Ответ: 1) 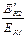 =1; 2)
=1; 2) 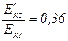 .
.
Дата добавления: 2020-10-25; просмотров: 724;











