Контрольные задания
1.1. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. Какой путь пройдет тело: 1) за первую 0,1 с своего движения, 2) за последнюю 0,1 с своего движения? Считать 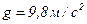 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.
1.2. Тело падает вертикально с высоты 19,6 м с нулевой начальной скоростью. За какое время тело пройдет: 1) первый 1 м своего пути, 2) последний 1 м своего пути? Считать 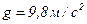 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.
1.3. С башни в горизонтальном направлении брошено тело с начальной скоростью 10 м/с. Пренебрегая сопротивлением воздуха, определите для момента времени 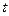 = 2 с после начала движения: 1) скорость тела; 2) радиус кривизны траектории. Считать
= 2 с после начала движения: 1) скорость тела; 2) радиус кривизны траектории. Считать 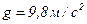 .
.
1.4. Камень брошен горизонтально со скоростью 5м/с. Определите нормальное и тангенциальное ускорения камня через 1 с после начала движения. Считать 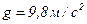 . Сопротивлением воздуха пренебречь.
. Сопротивлением воздуха пренебречь.
1.5. Материальная точка начинает двигаться по окружности радиусом 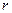 = 2,5 см с постоянным тангенциальным ускорением
= 2,5 см с постоянным тангенциальным ускорением 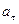 = 0,5 см/с2. Определите: 1) момент времени, при котором вектор ускорения
= 0,5 см/с2. Определите: 1) момент времени, при котором вектор ускорения 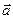 образует с вектором скорости
образует с вектором скорости 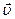 угол 45°; 2) путь, пройденный за это время движущейся точкой.
угол 45°; 2) путь, пройденный за это время движущейся точкой.
1.6. Зависимость пройденного телом пути от времени задаётся уравнением 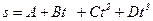 , где
, где 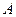 =0,1м,
=0,1м, 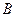 =0,1м/с,
=0,1м/с, 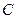 =0,14м/с2,
=0,14м/с2, 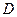 =0,01м/с3. 1) Через сколько времени после начала движения ускорение тела будет равно 1м/с2? 2) Чему равно среднее ускорение тела за этот промежуток времени?
=0,01м/с3. 1) Через сколько времени после начала движения ускорение тела будет равно 1м/с2? 2) Чему равно среднее ускорение тела за этот промежуток времени?
1.7. Зависимость пройденного телом пути от времени задаётся уравнением 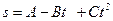 , где
, где 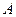 =5м,
=5м, 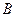 =4м/с,
=4м/с, 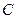 =1м/с2. Запишите выражения для скорости и ускорения. Определите для момента времени
=1м/с2. Запишите выражения для скорости и ускорения. Определите для момента времени 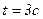 после начала движения пройденный путь, скорость и ускорение.
после начала движения пройденный путь, скорость и ускорение.
1.8. Зависимость пройденного телом пути 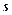 от времени
от времени 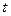 выражается уравнением
выражается уравнением 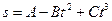 (
( 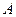 = 2 м/с,
= 2 м/с, 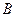 = 3 м/с2,
= 3 м/с2, 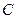 = 4 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени
= 4 м/с3). Запишите выражения для скорости и ускорения. Определите для момента времени 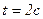 после начала движения пройденный путь, скорость и ускорение.
после начала движения пройденный путь, скорость и ускорение.
1.9. Нормальное ускорение точки, движущейся по окружности радиусом 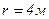 , задается уравнением
, задается уравнением 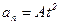 , где
, где 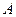 = 4 м/с4. Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время
= 4 м/с4. Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время 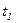 = 5 с после начала движения; 3) полное ускорение для момента времени
= 5 с после начала движения; 3) полное ускорение для момента времени 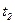 = 1 с.
= 1 с.
1.10. Кинематические уравнения движения двух материальных точек имеют вид 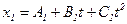 и
и 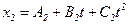 , где
, где 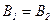 ,
, 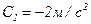 ,
, 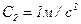 . Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения
. Определите: 1) момент времени, для которого скорости этих точек будут равны; 2) ускорения 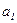 и
и 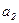 для этого момента.
для этого момента.
1.11. Диск радиусом 10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 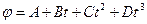 (
( 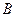 = 1 рад/с,
= 1 рад/с, 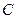 = 1 рад/с2,
= 1 рад/с2, 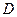 = 1 рад/с3). Определите для точек на ободе диска к концу второй секунды после начала движения тангенциальное, нормальное и полное ускорения.
= 1 рад/с3). Определите для точек на ободе диска к концу второй секунды после начала движения тангенциальное, нормальное и полное ускорения.
1.12. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 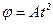 (
( 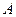 =0,5 рад/с2). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения.
=0,5 рад/с2). Определите к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное, нормальное и полное ускорения.
1.13. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 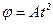 (
( 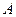 =0,1рад/с2). Определите полное ускорение точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки 0,4 м/с.
=0,1рад/с2). Определите полное ускорение точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки 0,4 м/с.
1.14. Диск радиусом 0,2 м вращается вокруг неподвижной оси так, что зависимость угловой скорости от времени задается уравнением 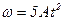 , где
, где 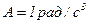 . Определите для точек на ободе диска к концу первой секунды после начала движения полное ускорение и число оборотов, сделанных диском за первую минуту движения.
. Определите для точек на ободе диска к концу первой секунды после начала движения полное ускорение и число оборотов, сделанных диском за первую минуту движения.
1.15. Диск радиусом 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением 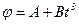 (
( 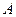 = 2 рад,
= 2 рад, 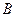 = 4 рад/с3). Определите для точек на ободе колеса: 1) нормальное ускорение в момент времени 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота, при котором полное ускорение составляет с радиусом колеса 45°.
= 4 рад/с3). Определите для точек на ободе колеса: 1) нормальное ускорение в момент времени 2 с; 2) тангенциальное ускорение для этого же момента; 3) угол поворота, при котором полное ускорение составляет с радиусом колеса 45°.
1.16. Якорь электродвигателя, имеющий частоту вращения 50 с-1, после выключения тока, сделав 628 оборотов, остановился. Определите угловое ускорение якоря.
1.17. Колесо автомобиля вращается равноускоренно. За время 2 мин оно изменило частоту вращения от 60 до 240 мин-1. Определите: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время.
1.18. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найдите угловое ускорение колеса.
1.19. Колесо спустя 1 мин после начала вращения приобретает скорость, соответствующую частоте 720 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных колесом за эту минуту. Движение считать равноускоренным.
1.20. Колесо, вращаясь равнозамедленно, при торможении уменьшило частоту вращения за 1 мин с 300 об/мин до 180 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных за это время.
3. Динамика материальной точки и поступательного
движения твердого тела
Основные формулы
· Импульс материальной точки:

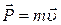 ,
,
где 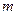 -масса материальной точки,
-масса материальной точки, 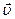 - скорость движения.
- скорость движения.
· Второй закон Ньютона (основное уравнение динамики материальной точки):
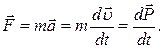
· Это же уравнение в проекциях на касательную и нормаль к траектории движения точки:
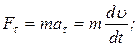
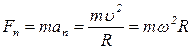 ,
,
где 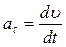 – тангенциальное (касательное) ускорение,
– тангенциальное (касательное) ускорение,
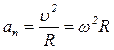 – нормальное (центростремительное) ускорение.
– нормальное (центростремительное) ускорение.
· Сила трения скольжения:
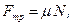
где 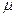 – коэффициент трения скольжения;
– коэффициент трения скольжения; 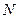 – сила нормального давления.
– сила нормального давления.
· Сила упругости:
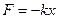 ,
,
где 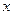 - величина деформации;
- величина деформации; 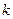 - коэффициент жесткости.
- коэффициент жесткости.
· Сила гравитационного притяжения двух материальных точек:
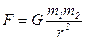 ,
,
где 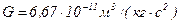 – гравитационная постоянная,
– гравитационная постоянная,
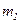 и
и 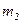 – массы взаимодействующих точек,
– массы взаимодействующих точек, 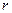 – расстояние между точками.
– расстояние между точками.
· Закон сохранения импульса для замкнутой системы:
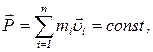
где 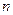 - число материальных точек (или тел), входящих в систему.
- число материальных точек (или тел), входящих в систему.
· Работа, совершаемая телом
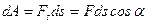 ,
,
где 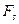 — проекция силы на направление перемещения;
— проекция силы на направление перемещения; 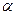 — угол между направлениями силы и перемещения.
— угол между направлениями силы и перемещения.
· Работа, совершаемая переменной силой, на пути 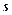 :
:
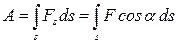
· Средняя мощность за промежуток времени 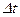 :
:
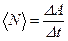 ,
,
где 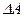 – работа за промежуток времени
– работа за промежуток времени 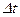 .
.
· Мгновенная мощность:
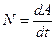 , или
, или 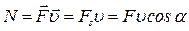 .
.
· Кинетическая энергия движущегося со скоростью 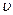 тела
тела
массой 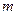 :
:
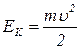 .
.
· Потенциальная энергия тела массой 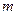 , поднятого над поверхностью земли на высоту
, поднятого над поверхностью земли на высоту 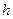 :
:
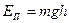 ,
,
где 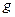 – ускорение свободного падения.
– ускорение свободного падения.
· Потенциальная энергия упруго деформированного тела:
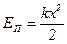 .
.
· Потенциальная энергия гравитационного взаимодействия:
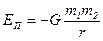 .
.
· Закон сохранения механической энергии (для консервативной системы):
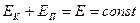 .
.
Дата добавления: 2020-10-25; просмотров: 643;











