Робота електричного поля по переміщенню заряду. Потенціал
При переміщенні пробного зарядуq в електростатичному полі електричні сили здійснюють роботу (рис. 3.11). Ця робота при малому переміщенні Δl становить:
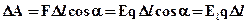 . (3.11)
. (3.11)
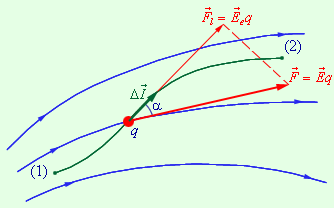
Рисунок 3.11.
Розглянемо роботу сил електростатичного поля по переміщенню точкового заряду.
 На рисунку 3.12 зображені силові лінії кулонівського поля точкового заряду Qі дві різні траєкторії переміщення пробного заряду q з початкової точки (1) в кінцеву точку (2). На одній з траєкторій виділено мале переміщення Δl. Елементарна робота ΔA кулонівських сил на цьому переміщенні дорівнює:
На рисунку 3.12 зображені силові лінії кулонівського поля точкового заряду Qі дві різні траєкторії переміщення пробного заряду q з початкової точки (1) в кінцеву точку (2). На одній з траєкторій виділено мале переміщення Δl. Елементарна робота ΔA кулонівських сил на цьому переміщенні дорівнює:
. (3.12)

Рисунок 3.12.
 Якщо вираз (3.12) проінтегрувати на інтервалі від r = r1 до r = r2, отримаємо повну роботу:
Якщо вираз (3.12) проінтегрувати на інтервалі від r = r1 до r = r2, отримаємо повну роботу:
. (3.13)
Отриманий результат не залежить від форми траєкторії. На траєкторіях I і II, зображених на рисунку 3.12, роботи кулонівських сил однакові. Якщо на одній з траєкторій змінити напрям переміщення заряду q на протилежне, то робота змінить знак. Звідси витікає, що на замкнутій траєкторії робота кулонівських сил дорівнює нулю.
Отже електростатичне поле має важливу властивість:
Робота сил електростатичного поля при переміщенні заряду з однієї точки поля в іншу не залежить від форми траєкторії, а визначається тільки положенням початкової і кінцевої точок і величиною заряду.
Наслідком незалежності роботи від форми траєкторії є наступне твердження:
Робота сил електростатичного поля при переміщенні заряду по будь-якій замкнутій траєкторії дорівнює нулю.
Силові поля, що мають цю властивість, називають потенціальними або консервативними.
В тому випадку, коли електростатичне поле створюється сукупністю точкових зарядів Qi, то при переміщенні пробного заряду q робота результуючого поля A відповідно до принципу суперпозиції складатиметься з робіт Ai кулонівських полів точкових зарядів:
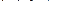 .
.
Оскільки кожен член суми Ai не залежить від форми траєкторії, то і повна робота A результуючого поля не залежить від шляху і визначається тільки положенням початкової і кінцевої точок.
Властивість потенціальності електростатичного поля дозволяє ввести поняття потенціальної енергії заряду в електричному полі.
Для цього в просторі вибирається деяка точка (0), і потенціальна енергія заряду q, поміщеного в цю точку, приймається рівною нулю.
Потенціальна енергія заряду q, поміщеного в будь-яку точку (1) простору, відносно фіксованої точки (0) дорівнює роботі A10, яку виконає електричне поле при переміщенні заряду q з точки (1) в точку (0):
Wp1 = A10.
(В електростатиці енергію прийнято означати буквою W, оскільки буквою E позначають напруженість поля.)
Так само, як і в механіці, потенціальна енергія визначена з точністю до сталої величини, залежної від вибору опорної точки (0). Така неоднозначність у визначенні потенціальної енергії не призводить до яких-небудь непорозумінь, оскільки фізичний зміст має не сама енергія, а різниця її значень в двох точках простору.
Робота, що здійснюється електричним полем при переміщенні точкового заряду q з точки (1) в точку (2), дорівнює різниці значень потенціальної енергії в цих точках і не залежить від шляху переміщення заряду і від вибору точки (0).
A12 = A10 + A02 = A10 - A20 = Wp1 - Wp2.(3.14)
 Фізичну величину, рівну відношенню потенціальної енергії електричного заряду в електростатичному полі до величини цього заряду, називають потенціалом φ електричного поля :
Фізичну величину, рівну відношенню потенціальної енергії електричного заряду в електростатичному полі до величини цього заряду, називають потенціалом φ електричного поля :
. (3.15)
Потенціал φ є енергетичною характеристикою електростатичного поля.
Робота A12 по переміщенню електричного заряду q з початкової точки (1) в кінцеву точку (2) дорівнює добутку заряду на різницю потенціалів (φ1 - φ2) початкової і кінцевої точок
A12 = Wp1 - Wp2 = qφ1 - qφ2 = q(φ1 - φ2).(3.16)
У Міжнародній системі одиниць (СІ) одиницею потенціалу являється вольт (В).
1 В = 1 Дж / 1 Кл.
У багатьох завданнях електростатики при обчисленні потенціалів за опорну точку (0) зручно прийняти нескінченно віддалену. В цьому випадку поняття потенціалу може бути визначене таким чином:
 Потенціал поля в заданій точці простору дорівнює роботі, яку здійснюють електричні сили пр переміщенні одиничного позитивного заряду з цієї точки в безкінченність.
Потенціал поля в заданій точці простору дорівнює роботі, яку здійснюють електричні сили пр переміщенні одиничного позитивного заряду з цієї точки в безкінченність.
Для наочного представлення електричного поля разом з силовими лініями використовують еквіпотенціальні поверхні.
Поверхня, в усіх точках якої потенціал електричного поля має однакові значення, називається еквіпотенціальною поверхнею або поверхнею рівного потенціалу.
Силові лінії електричного поля завжди перпендикулярні еквіпотенціальним поверхням.
На рисунку 3.13 представлені картини силових ліній і еквіпотенціальних поверхонь деяких простих електростатичних полів.
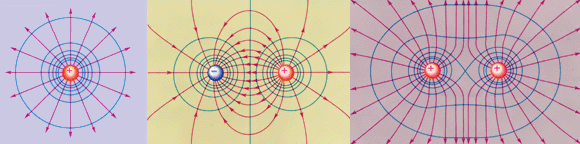
Рисунок 3.13.
Еквіпотенціальні поверхні (сині лінії) і силові лінії (червоні лінії) простих електричних полів : a - точковий заряд; b - електричний диполь; c - два рівні позитивні заряди.
У разі однорідного поля еквіпотенціальні поверхні є системою паралельних площин.
Якщо пробний заряд q переміщується на відстань Δr уздовж силової лінії з точки (1) в точку (2), то елементарна робота сил поля дорівнює:
ΔA12 = qEΔr= q(φ1 – φ2) = – qΔφ,

З відси слідує, що (3.17)
Вираз (3.17) в скалярній і векторній формі виражає зв'язок між напруженістю поля і потенціалом.
Потенціал φ поля точкового заряду Q на відстані r від нього відносно нескінченно віддаленої точки обчислюється таким чином:

. (3.18)
Як випливає з теореми Гауса, ця ж формула виражає потенціал поля рівномірно зарядженої кулі (чи сфери) при r ≥ R, де R - радіус кулі.
З принципу суперпозиції напруженості електричного поля, слідує принцип суперпозиції для потенціалів:
φ = φ1 + φ2 + φ3 + ..
Дата добавления: 2020-10-25; просмотров: 974;











