Корпускулярно-волновой дуализм материи. Соотношение неопределенностей. Предмет квантовой механики

В первой трети 20-го века в физике произошла революция, оказавшая огромное влияние на последующее развитие всего естествознания. Одним из основных результатов этой революции явилось создание теории относительности (см. главу 3), вторым - создание квантовой физики и ее ядра - квантовой механики. Важнейший вклад в разработку квантовой механики внесли М. Планк (нем.), А. Эйнштейн (нем.), Н. Бор (дат.), Л. де Бройль (фр.), Э. Шрёдингер (австр.), В. Гейзенберг (нем.), В. Паули (нем.), П. Дирак (англ.) и др.

Впервые квантовые представления были введены в 1900 г. М. Планком в работе, посвященной тепловому излучению тел (Нобелевская премия 1918 г.). Существовавшая к тому времени теория теплового излучения, основанная на классической электродинамике и статистической физике, не могла объяснить свойства и установленные на опыте законы этого излучения. Планк разрешил эту проблему и получил прекрасно согласующиеся с опытом результаты, предположив, что свет испускается не непрерывно, как это предполагается в классической теории излучения, а дискретными порциями энергии - квантами. Величина кванта энергии зависит от частоты 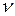света и рассчитывается по формуле Планка

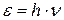, (9.1)

где h=6.63·10^-34 Дж·с - постоянная Планка, иногда называемая квантом действия.

Квантовая гипотеза Планка получила развитие в работе А. Эйнштейна 1905 года (Нобелевская премия 1921 г.), в которой была дана теория фотоэффекта, то есть выбивания электронов из вещества под действием света. Развивая идею Планка, Эйнштейн предположил, что свет не только испускается и поглощается, но и распространяется квантами, то есть что дискретность присуща не процессу излучения и поглощения, а самому свету. По Эйнштейну свет состоит из отдельных квазичастиц («как бы частиц»), названных фотонами. Энергия фотона определяется формулой Планка (9.1).

Экспериментальное подтверждение квантовой природы света получил в 1922 г. А. Комптон (амер., Нобелевская премия 1927 г.) в опытах по рассеянию рентгеновского излучения веществом, содержащем слабо связанные (почти свободные) электроны. Комптон обнаружил, что длина волны излучения при рассеянии увеличивается, что не могла объяснить классическая теория рассеяния волн. Однако этот эффект (эффект Комптона) вполне объясним, если рассматривать рассеяние света как результат абсолютно упругого соударения двух частиц: фотона и электрона. При таком соударении должны выполняться законы сохранения энергии и импульса, то есть фотон, наряду с энергией, обладает и импульсом.

Поскольку фотон движется со скоростью света, то его движение должно описываться специальной теорией относительности (см. подраздел 3.2). Как отмечалось в 3.2, двигаться со скоростью света могут только частицы с нулевой массой покоя. Следовательно, масса покоя фотона 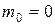и существовать он может, только двигаясь со скоростью света. Замедлить свое движение или, тем более, остановиться он не может. Но фотон обладает релятивистской массой (массой движения), равной согласно формуле (3.13)

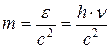, (9.2)

и релятивистским импульсом, равным в соответствии с (3.12), (9.2), (8.2) и (8.5)

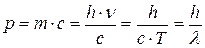. (9.3)

Используя формулы (9.1)-(9.3) в законах сохранения энергии и импульса применительно к упругому соударению фотона и электрона, Комптон смог объяснить закономерности наблюдавшегося им эффекта.

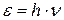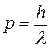Этот эксперимент и ряд других доказали, что свет наряду с волновыми свойствами, проявляющимися, например, в явлениях интерференции и дифракции, обладает и корпускулярными свойствами: он как бы состоит из частиц - фотонов. Такая двойственность природы света получила название корпускулярно-волнового дуализма света. Дуализм содержится уже в формулах (9.1) и (9.3): и , не позволяющих выбрать одну из двух концепций (корпускулярную или волновую, иначе говоря, континуальную) для описания свойств света. Энергия 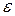и импульс p - характеристики частицы, частота 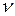и длина волны 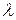- характеристики волны. Возникло формальное противоречие: для объяснения одних явлений нужно было считать, что свет имеет волновую природу, а для объяснения других - корпускулярную. Разрешение этого противоречия и привело к созданию физических основ квантовой механики.

В 1924 г. Л. де Бройль (Нобелевская премия 1929 г.) выдвинул гипотезу о том, что корпускулярно-волновой дуализм присущ не только свету, но и вообще всей материи. Согласно де Бройлю, каждой частице независимо от ее природы следует поставить в соответствие волну, длина которой 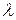связана с импульсом p частицы соотношением, аналогичным соотношению (9.3):

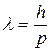. (9.4)

Эта формула была названа формулой де Бройля, а волны, соответствующие частицам, - волнами де Бройля.

Почему мы не замечаем наличия волновых свойств у окружающих нас макроскопических предметов? Для ответа на этот вопрос рассмотрим очень маленький макрообъект - пылинку массой m=1нг=10^-12 кг, движущуюся с малой скоростью 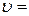0.001 мм/с=10^-6 м/с. Её импульс 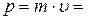10^-18 кг·м/с, а длина волны де Бройля, как следует из формулы (9.4), равна 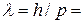6.63·10^-16 м, что намного меньше размеров атома (~10^-10 м). Увеличение массы или скорости тела ведет к дальнейшему уменьшению длины волны де Бройля. Следовательно, для макрообъектов длина волны де Бройля чрезвычайно мала, обнаружить волновые свойства таких объектов практически невозможно, и их можно не учитывать. Рассмотрим теперь микрообъект, например электрон массой m=9.1·10^-31 кг, движущийся с вполне обычной для электрона скоростью 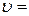10⁶ м/с. Для него длина волны де Бройля 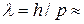7·10^-10 м, что соизмеримо с размерами атома или межатомным расстоянием в молекуле или в кристаллической решетке. Поэтому при изучении движения микрообъектов – элементарных частиц в атомах, атомных ядрах, молекулах, в кристаллической решетке волновые свойства учитывать необходимо.

То, что не только фотоны, но и все «обыкновенные» частицы (электроны, протоны и др.) обладают волновыми свойствами, должно, в частности, проявляться в дифракции частиц. В 1927 г. К. Дэвиссон и Л. Джермер (амер., Нобелевская премия 1937 г.) впервые наблюдали дифракцию электронов, использовав в качестве дифракционной решетки кристаллическую решетку металла (никеля). Позднее волновые свойства были обнаружены и у других частиц. Справедливость гипотезы де Бройля и формулы (9.4) была убедительно подтверждена множеством экспериментов.

Наличие у микрочастиц волновых свойств делает невозможным применение в микромире многих понятий классической физики. Так, в классической механике состояние частицы характеризуют ее координаты и ее импульс или скорость (см. подраздел 5.2). При этом считается очевидным, что координаты частицы и ее импульс могут быть в принципе определены одновременно сколь угодно точно. Оказывается, что для микрочастиц это неверно в принципе: координаты частицы x, y, z и соответствующие проекции ее импульса 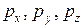не могут иметь одновременно определенные значения. Для того, чтобы понять это парадоксальное утверждение, рассмотрим мысленный эксперимент Гейзенберга, схема которого представлена на рисунке 9.1.

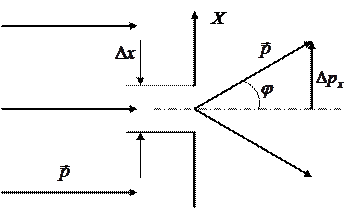
Рисунок 9.1 - Схема мысленного эксперимента к выводу соотношения неопределенностей.

Пусть перпендикулярно оси OX движется поток частиц с импульсами 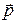. Поскольку по условию импульс 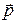перпендикулярен оси OX, то проекция на ось OX импульса каждой частицы вполне определена: 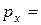0, но координата x отдельно взятой частицы может принимать произвольное значение: 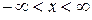(полная неопределенность координаты x). Совместим с осью OX экран с щелью шириной 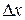(щель перпендикулярна плоскости рисунка 9.1). При прохождении частицы сквозь щель неопределенность координаты x частицы уменьшается от бесконечности до 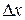, но вследствие дифракции (огибания краев препятствия частицами из-за наличия у них волновых свойств) направление движения отдельно взятой частицы становится неопределенным и возникает неопределенность проекции импульса 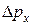. Найдя по формуле де Бройля (9.4) длину волны, соответствующей частице, с помощью теории волн можно определить угол дифракции 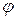и показать, что неопределенности координаты 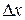и проекции импульса 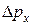частицы связаны соотношением

.

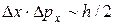Более строгий расчет приводит к соотношению

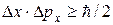, (9.5)

где 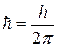=1.05·10^-34 Дж·с - постоянная Планка, деленная на .

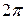Соотношение (9.5) было получено в 1927 г. В. Гейзенбергом (Нобелевская премия 1932 г.) и называется соотношением неопределенностей Гейзенберга.

Из (9.5) следует, что повышение точности определения координаты x частицы, то есть уменьшение неопределенности координаты 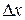, с неизбежностью ведет к увеличению неопределенности проекции импульса 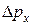, то есть уменьшению точности определения проекции импульса 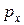. Одновременно точно определить x и 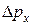нельзя, так как при этом 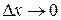и , и 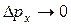, и неравенство (9.5) нарушается.

Аналогичное (9.5) соотношение существует для координаты y (или z) и соответствующей проекции импульса 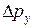(или 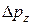). Кроме того, оказывается, что нельзя определить точно энергию E частицы в каком-либо состоянии и при этом точно знать время 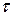пребывания частицы в этом состоянии. Неопределенности этих величин также связаны соотношением неопределенностей

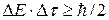. (9.6)

Вышеописанный мысленный эксперимент и соотношение (9.5) убеждают нас в том, что принятый в классической механике способ описания состояния частицы путем задания ее координат и импульса принципиально неприменим к микрочастицам.

Соотношения неопределенностей Гейзенберга (9.5), (9.6) являются математическими выражениями одного из принципиальных положений квантовой механики - принципа дополнительности, сформулированного Н. Бором. Согласно этому принципу, получение экспериментальных данных об одних физических величинах, описывающих микрообъект (элементарную частицу, атом, молекулу), неизбежно связано с потерей информации о некоторых других величинах, дополнительных к первым. Такими взаимно дополнительными величинами, как следует из соотношений неопределенностей, являются, например, координаты частицы и ее импульс (или скорость), энергия некоторого состояния и время пребывания в этом состоянии. Другими парами взаимно дополнительных величин являются кинетическая и потенциальная энергии, напряженность электрического поля и число фотонов и др.

Принцип дополнительности пытались объяснить влиянием измерительного прибора, всегда являющегося макроскопическим объектом, на состояние микрообъекта. Так, в вышеописанном мысленном эксперименте помещение экрана с щелью на пути потока частиц вызвало появление у них неопределенности импульса. Отсюда следовал вывод, что неизбежное влияние наблюдателя и измерительных инструментов на исследуемый объект делает принципиально невозможным получение объективной информации об объекте.

Однако современная квантовая теория измерений считает принцип дополнительности не выражением невозможности получения полной информации об объекте, а отражением объективных свойств самих квантовых систем. То есть принцип дополнительности говорит не о технической невозможности одновременного измерения взаимно дополнительных величин, а о том, что у этих величин на самом деле нет одновременно определенных значений.

Где проходит граница между классической механикой и механикой, учитывающей волновые свойства частиц? Волновые свойства частиц необходимо учитывать, если длина волны, соответствующей частице, соизмерима с размерами системы, структуры, в которой находится данная частица. Учет волновых свойств совершенно необходим при изучении движения электронов в атомах, молекулах и в кристаллической решетке, движения протонов и нейтронов в ядрах, при решении других задач, относящихся к физике микромира. В то же время, при изучении движения микрочастиц в макроскопических системах зачастую, как, например, при изучении движения электронов в электронно-лучевой трубке (кинескопе), волновые свойства частиц роли не играют, и они могут рассматриваться как материальные точки.

Раздел физики, изучающий движение и взаимодействие частиц с учетом их волновых свойств, называется квантовой механикой. Квантовая механика – механика микромира.

Квантовая механика подразделяется на нерелятивистскую, изучающую движения частиц со скоростями, много меньшими скорости света, и релятивистскую, изучающую движения с околосветовыми скоростями.

Квантовая механика не отрицает классическую механику, но ограничивает область ее применения. Как требует принцип соответствия (см. подраздел 3.2), эта новая теория включает в себя старую как предельный случай. Результаты квантовой механики совпадают с классическими, если длина волны, соответствующей рассматриваемому телу, пренебрежимо мала ( 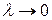). Объектом изучения классической механики остались движения макроскопических тел со сравнительно малыми скоростями.