Функция и ее статистический смысл. Принцип суперпозиции в квантовой механике

Важнейшим для понимания сути квантовой механики является вопрос об описании состояния микрочастиц. Способ описания состояния частицы, принятый в классической механике и заключающийся в задании координат и импульса (или скорости) частицы, в данном случае не годится, поскольку не учитывает волновые свойства микрочастицы. Решение данной проблемы связано с выяснением физического смысла волн де Бройля.

Рассмотрим мысленный эксперимент по распространению света (рисунок 9.2), то есть потока фотонов - частиц, сочетающих в себе корпускулярные и волновые свойства. Пусть на пути светового пучка находится полупрозрачная пластинка, отражающая, например, 30% и пропускающая 70% световой энергии. Что происходит с фотонами при попадании на пластинку? Отдельный фотон не может отразиться на 30%, а на 70% пройти сквозь пластинку. Не может он и разделиться на два фотона: «отраженный», забирающий 30% энергии, и «прошедший», обладающий 70% энергии падающего фотона. 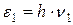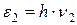Разделение фотона невозможно, так как энергии и «отраженного» и «прошедшего» фотонов, а, стало быть, частоты и длины волн отраженного и прошедшего света будут иными, чем у падающего, чего в действительности нет. Итак, фотон либо полностью отражается, либо полностью проходит. Зная коэффициент отражения пластинки, приходим к заключению, что 30% падающих фотонов отражаются, а 70% проходят сквозь пластинку. Получается парадоксальный с точки зрения классической механики результат: совершенно одинаковые частицы в одинаковых условиях ведут себя по-разному: либо отражаются, либо проходят сквозь пластинку. Мы приходим к важнейшему для понимания сути квантовой механики выводу: движение микрочастиц не имеет строго предопределенного, детерминированного характера, оно, напротив, имеет вероятностный характер. Так, в рассмотренном примере, если говорить об одном отдельно взятом фотоне, то заранее предсказать, отразится он от пластинки или пройдет сквозь нее, невозможно. Однако можно сказать, что вероятность отражения составляет 30%, а прохождения - 70%.

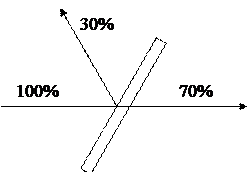
Рисунок 9.2 - Прохождение света через полупрозрачную пластинку.

Анализ вышеописанного мысленного эксперимента и других, в том числе реальных, экспериментов по дифракции, интерференции микрочастиц ведет к следующему статистическому (вероятностному) истолкованию физической природы волн де Бройля. Волна де Бройля является «волной вероятности» в том смысле, что ее интенсивность в каждой точке пространства является мерой вероятности обнаружения частицы в данной точке. Интенсивность же волны, как известно из теории волн, пропорциональна квадрату ее амплитуды.

В квантовой механике для описания состояния частицы используется так называемая волновая функция 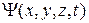или 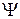-функция («пси-функция»). При этом определение дается не самой волновой функции, а квадрату ее модуля. Это делается следующим образом. Обозначим через dP вероятность того, что частица в момент времени t находится в бесконечно малом (элементарном) объеме dV пространства, окружающем точку с координатами x, y, z. Квадрат модуля 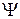-функции по определению есть отношение вероятности к объему 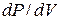, то есть плотность вероятности 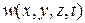нахождения частицы в объеме dV:

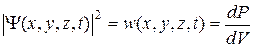. (9.7)

Из (9.7) следует, что вероятность 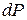равна произведению объема dV на квадрат модуля 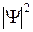волновой функции:

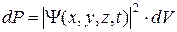. (9.8)

Такое статистическое толкование волновой функции, предложенное в 1826 г. М. Борном (нем.-англ., Нобелевская премия 1954 г.) лежит в основе квантовомеханического описания состояния микрочастиц.

Итак, дать квантовомеханическое описание состояния частицы означает определить ее волновую функцию, описывающую с помощью соотношения (9.8) вероятность нахождения частицы в каждом элементарном объеме пространства. Такое описание принципиально отличается от классического своим вероятностным характером.

В силу этого теряет смысл классическое определение траектории как совокупности точек пространства, проходимых частицей при ее движении. В квантовой механике под траекторией понимают совокупность точек, в которых вероятность нахождения частицы максимальна.

Принцип механического детерминизма и вообще механистическая парадигма в квантовой механике неприменимы.

Представление о мире, как огромном механизме, каждая «деталь» которого движется по строго предопределенной траектории, в котором нет места случайностям, флуктуациям, явлениям вероятностного характера, было поколеблено статистической физикой и окончательно отвергнуто квантовой механикой. Движение (развитие) в системах из большого числа частиц, изучаемое статистической физикой, и движение в микромире, изучаемое квантовой механикой, имеют вероятностный характер, но подчиняются статистическим закономерностям.

Выражением этих закономерностей является открытое в 1926 г. Э. Шрёдингером (Нобелевская премия 1933 г.) уравнение для расчета волновой функции 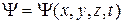микрочастицы, движущейся во внешнем силовом поле:

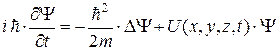, (9.9)

где 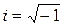- мнимая единица, 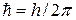, m - масса частицы, 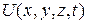- традиционное для квантовой физики обозначение потенциальной энергии частицы в точке с координатами x, y, z в момент t, 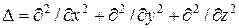- оператор Лапласа.

Уравнение Шрёдингера (9.9) применимо для расчета волновых функций частиц, движущихся гораздо медленнее света, поэтому является основным уравнением нерелятивистской квантовой механики. В 1928 г. П. Дирак (Нобелевская премия 1933 г.) предложил другое уравнение, описывающее движение микрочастиц с околосветовыми скоростями и являющееся основным уравнением релятивистской квантовой механики.

Подчеркнем, что уравнения Шрёдингера и Дирака, подобно законам Ньютона, отражают базовые, основные закономерности природы, не сводящиеся к каким-то еще более основным. Поэтому уравнения Шредингера и Дирака, как и законы Ньютона, были именно открыты, а не выведены из других уравнений и законов. Справедливость этих уравнений доказывается проверкой на опыте выводов и результатов, следующих из этих уравнений.

Если известна волновая функция частицы, то по несложным правилам, установленным в квантовой механике, могут быть найдены основные механические характеристики ее движения: импульс, момент импульса, кинетическая и потенциальная энергия.

Во многих случаях уравнение (9.9) имеет не единственное решение, а несколько или даже бесконечно много решений, то есть имеется несколько (бесконечно много) различных 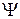-функций, удовлетворяющих уравнению (9.9). Это означает, что частица может находиться не в одном, а в различных состояниях, каждому из которых соответствует своя волновая функция 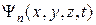, где n - номер состояния.

В квантовой механике важную роль играет принцип суперпозиции (см. подраздел 5.2). Но если в классической физике принцип суперпозиции выполняется только при определенных условиях, то в квантовой физике - это фундаментальный принцип, один из основных постулатов, определяющих вместе с принципом неопределенности всю структуру теории. Принцип суперпозиции в квантовой физике гласит: если квантовомеханическая система может находиться в состояниях, описываемых волновыми функциями 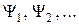, то она может также находиться и в состоянии, описываемом волновой функцией

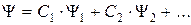, (9.10)

где 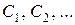- не зависящие от координат числа, квадрат модуля каждого из которых равен вероятности обнаружить в эксперименте частицу в состоянии с номером 1, 2 и т.д., соответственно.