Теория строения атомов Бора. Квантовая теория строения атомов. Спин микрочастиц

Параллельно развитию представлений о корпускулярно-волновом дуализме материи в физике развивалось другое направление, также способствовавшее созданию квантовой механики. Речь идет о теории строения атомов. В результате опытов Э. Резерфорда (англ., Нобелевская премия по химии 1908 г.) по рассеянию 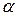-частиц атомами металлической пленки (1911 г.) в физике была принята планетарная модель строения атома. Согласно этой модели, в центре атома находится положительно заряженное ядро, в котором сосредоточена почти вся масса атома; вокруг ядра по орбитам вращаются отрицательно заряженные электроны. Однако эта модель противоречила классической физике. Согласно классической электродинамике, вращающийся по орбите электрон должен излучать электромагнитную волну и, следовательно, терять энергию; в результате электрон должен за малое время упасть на ядро, чего в действительности не происходит.

Пытаясь разрешить это противоречие, Н. Бор (Нобелевская премия 1922 г.) в 1913 г. создал свою теорию строения простейших (водородоподобных) атомов и ионов, имеющих единственный электрон, в которой он идею Планка о квантовании энергии попытался применить в атомной физике. Он постулировал, что существуют определенные, так называемые стационарные орбиты, двигаясь по которым вокруг ядра, электрон не излучает и не поглощает энергии. Каждой из стационарных орбит соответствует определенное значение энергии движущегося по орбите электрона 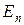(n=1, 2, 3, ... - номер орбиты). По второму постулату Бора при скачкообразном (квантовом) переходе электрона с одной орбиты на другую испускается или поглощается квант энергии. Если энергия 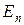на орбите номер n, с которой переходит электрон, больше энергии 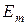на орбите номер m, на которую электрон переходит, то испускается квант с энергией

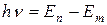, (9.11)

если энергия 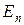на исходной орбите меньше энергии 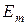электрона на конечной орбите, то для перехода требуется поглощение кванта энергии

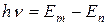. (9.12)

По условию квантования орбит, предложенному Бором, стационарными являются те орбиты, при движении по которым момент импульса 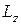электрона относительно оси его вращения по орбите (о моменте импульса см. подраздел 6.2) принимает значения, кратные постоянной Планка :

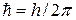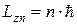, (9.13)

где n=1, 2, ... - номер орбиты.

На основе этих постулатов Бор рассчитал значения энергии 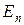(n=1, 2, ...), которые может иметь электрон в простейших атомах и ионах, частоты и длины волн, испускаемых при различных переходах в таких атомах и ионах. Расчетные значения длин волн отлично соответствовали данным экспериментов по изучению спектров излучения атомов и ионов.

Принципиально важным моментом теории Бора является идея о квантованности таких физических величин как энергия, момент импульса. Если в классической механике энергия и момент импульса тела, вращающегося вокруг оси, в принципе могут изменяться непрерывно и принимать любые значения от нуля до очень больших величин, то в квантовой механике эти же величины для электрона, вращающегося вокруг ядра, могут принимать только некоторые, «разрешенные» значения, каждое из которых соответствует движению по определенной орбите. Такие величины, которые могут принимать только определенные дискретные разрешенные значения, называются квантованными, а совокупность этих разрешенных значений называется спектром значений данной величины. Например, набор разрешенных значений энергии 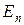образует энергетический спектр электрона в атоме.

Теория Бора была внутренне противоречива, поскольку сочетала в себе элементы новой теории (квантование орбит, испускание и поглощение квантов энергии) с приемами классической механики (электрон рассматривался как материальная точка, движущаяся по траектории вокруг ядра под действием силы электрического притяжения). Полностью непротиворечивую теорию строения атомов можно создать только путем последовательного применения квантовой механики.

Для этого необходимо с помощью уравнения Шредингера, используя в нем формулу (6.21) потенциальной энергии взаимодействия электрона и ядра, определить волновые функции электронов, движущихся в электрическом поле положительно заряженного ядра. Эта задача точно решается только для водородоподобных атомов и ионов, у которых вокруг ядра движется единственный электрон (атом H, ионы He⁺, Li²⁺). Для более сложных атомов и ионов с двумя и более электронами получены приближенные решения.

Основные результаты квантовой теории строения атомов таковы.

Одноэлектронный атом может находиться в определенных квантовых состояниях, каждому из которых соответствует своя 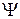-функция, то есть свое пространственное распределение плотности вероятности нахождения электрона. Состояние электрона, то есть вид 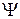-функции, определяется тремя целочисленными параметрами, называемыми квантовыми числами. Главное квантовое число n принимает значения 1, 2, 3 ... , орбитальное квантовое число l при заданном значении n принимает значения 0, 1, ... 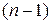, магнитное квантовое число m при заданном значении l принимает значения .

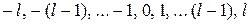Для одноэлектронных атомов и ионов их энергия в каждом из возможных состояний определяется только главным квантовым числом. Эти разрешенные значения энергии таковы:

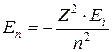, (9.14)

где Z - порядковый номер элемента в таблице Менделеева, 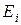=13.6 эВ - энергия ионизации атома водорода (1 эВ = 1.6·10^-19 Дж - электрон-вольт), смысл знака «-» в выражении для энергии объяснен в подразделе 6.3.

Орбитальное квантовое число l определяет численное значение орбитального момента импульса электрона:

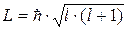, (9.15)

а магнитное число m определяет проекцию вектора орбитального момента импульса на некоторое направление в пространстве (ось OZ), то есть момент импульса относительно оси OZ:

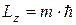. (9.16)

Некоторые расхождения теории и эксперимента привели к выводу, что электрон, кроме момента импульса, обусловленного вращением по орбите, должен обладать собственным моментом импульса, названным спином (от англ. spindle - веретено). Аналогично Земле, вращающейся по орбите вокруг Солнца и при этом вращающейся вокруг собственной оси, электрон также движется вокруг ядра и при этом как бы вращается вокруг собственной оси.

Подобно орбитальному моменту импульса, проекция спина 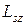на ось OZ также может принимать не любые, а только разрешенные значения:

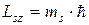, (9.17)

где 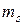- магнитное спиновое квантовое число, которое для электрона может принимать только два значения 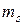= 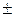1/2.

Таким образом, состояние электрона в атоме можно охарактеризовать, задав значения четырех квантовых чисел: .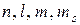

В многоэлектронных атомах состояние каждого из электронов также характеризует набор значений четырех квантовых чисел 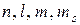, причем значения, которые могут принимать эти квантовые числа, определяются теми же правилами, что и для одноэлектронного атома.

Отметим, что представление о спине частиц как вращении вокруг собственной оси является упрощенным, используемым лишь для пояснения этого понятия. В действительности спин - собственный момент импульса частицы - является специфическим свойством микрочастиц, не имеющим прямых аналогий в макромире. Кроме электрона спином обладают многие другие частицы, в том числе – фотоны. Численное значение проекции спина микрочастицы 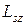может быть равно нулю, целому (1, 2, 3) или полуцелому (1/2, 3/2) числу квантов действия .

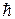Электроны и другие частицы с полуцелым спином относятся к классу частиц, называемых фермионами. Для фермионов справедлив принцип В. Паули, установленный в 1924-25 гг. (Нобелевская премия 1945 г.): в любой квантовой системе, например - в атоме, не может быть двух и более фермионов, находящихся в одинаковых состояниях, определяемых набором одинаковых значений всех четырех квантовых чисел.

С помощью принципа Паули объясняется распределение электронов по состояниям в многоэлектронных атомах, а тем самым объясняются химические свойства атомов, о чем будет рассказано в главах, посвященных основам химии.