Теория обнаружения сигналов
Классическая психофизика столкнулась с феноменом, который она не могла объяснить – феноменом ложной тревоги. Он состоит в том, что испытуемый дает ответ, что есть сигнал, когда после предупредительного сигнала раздражитель не подается. Исследователи не знали, что делать с этими ложными тревогами. Они пытались использовать испытуемых, дающих мало ложных тревог, просто исключали их из обработки.
Однако развитие радиолокации потребовало созданияе такой теории, которая учитывала бы ложные тревоги. Одна из таких теорий – теория обнаружения сигналов. Она была разработана в статистической радиотехнике и теории связи. Ее применили также и в области психологии, благодаря исследованиям целого ряда ученых, прежде всего, американских психологов — Таннера и Светса(W. Tanner, J. Swets). В соответствии с этой теорией сигнал всегда наблюдается на фоне шума. Шум возникает внутри самой сенсорной системы и создается внешними источниками. В зрительной системе шум возникает из–за собственного свечения сетчатки, в слуховой – из–за движении мышц при дыхании. Таким образом, сенсорная система вынуждена выделять сигнал из сенсорного шума. Величина шума воспринимаемая сенсорной системой, постоянно меняется, вызывая изменения сенсорного эффекта.
Обозначим зависимость плотности вероятности того или иного сенсорного эффекта (p), вызываемого шумом, от величины шума как функцию f (xn). Эта функция имеет нормальный вид (см. рис. 1).
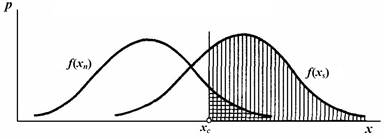
Рис. 1. Зависимость плотности вероятности сенсорного эффекта (p) от величины сенсорного эффекта (x), вызванного только шумом f (xn)и вызванного совместным действием сигнала и шумаf (xs).
Если испытуемому предъявлять сигнал постоянной интенсивности, то вызванный им сенсорный эффект будет суммироваться с сенсорным эффектом от шума. Соответственно, функция плотности вероятности появления сенсорного эффекта той или иной величины от этого сигнала будет описываться той же функцией f (xn), но смещенной по оси «х» вправо на величину сигнала. Обозначим эту функцию как f (xs). Из рисунка видно, что кривые этих двух функций перекрываются. На этом участке сенсорный эффект одной и той же величины может быть вызван в результате действия как сигнала вместе с шумом, так и одного только шума. Наблюдатель должен решить, результатом чего является наблюдаемый сенсорный эффект – результатом действия сигнала вместе с шумом или результатом действие одного только шума. Для решения этой задачи он выбирает для себя критерий – некоторое значение сенсорного эффекта (xс). Если наблюдаемый эффект выше критерия, он решает, что сигнал есть, а если ниже критерия – что сигнала нет, есть только шум. Возможны четыре варианта сочетания ситуации наличия или отсутствия сигнала с ответами наблюдателя:
1. Y/s – испытуемый говорит «да», когда есть сигнал (попадание, обнаружение).
2. N/s – испытуемый говорит «нет», когда есть сигнал (пропуск сигнала).
3. Y/n – испытуемый говорит «да», когда нет сигнала (ложная тревога).
4. Nn – испытуемый говорит «нет», когда нет сигнала (покой).
Каждый из вариантов характеризуется своей условной вероятностью Р:
1. Ys – P(Ys), 2. Ns – P(Ns), 3. Yn – P(Yn), 4. Nn – P(Nn).
Эти условные вероятности зависят от положения критерия xс на оси абсцисс. При стремлении снизить количество ложных тревог необходимо сместить xс вправо по оси абсцисс. Одновременно это приведет к увеличению числа пропусков и уменьшению числа обнаружений. Стремление к полному обнаружению сигнала приведет к увеличению ложных тревог.
Выбор критерия xс зависит от субъективной значимости каждого из четырех исходов. Если ни один из исходов не важнее, чем остальные исходы, то xс будет соответствовать точке пересечения кривых f (xn) и f (xs). Если наблюдателю надо избежать пропусков, то надо уменьшить xс, если нежелательны ложные тревоги, то надо увеличить xс. Оптимальное значение xс определяется из следующей формулы:
| b = | f (xs) | xc | = | P (n) | • | V (Nn) – C (Yn) | , |
| f (xn) | xc | P (s) | V (Ys) – C (Ns) |
Здесь: b - соотношение между уровнем сигнала и уровнем шума,
P (n) – априорные вероятности появления шума,
P (s) – априорные вероятности появления сигнала в смеси с шумом,
V (Nn) –премия за покой,
V (Ys) – премия за обнаружение сигнала,
C (Yn) – штраф за ложную тревогу,
C (Ns) – штраф за пропуск сигнала.
Критерии определенные по данной формуле обеспечивают наблюдателю величину наибольшего выигрыша. Американские психологи Таннер и Светс провели опыты в области слухового и зрительного обнаружения сигнала. До начала опыта испытуемым сообщались значения P(N) и P(S). Начисление премий и штрафов производилось с помощью платежной матрицы, которую показывали испытуемым:
| Ответ испытуемого | |||
| Да | Нет | ||
| Сигнал был? | Да | V (Ys) | C (Ns) |
| Нет | C (Yn) | V (Nn) |
Штрафы и премии оплачивались реальными деньгами. Эти опыты подтвердили теоретически предсказанные результаты.
Критерий напоминает сенсорный порог, но отличается от порога тем, что наблюдатель может изменять его произвольно, а порог изменять нельзя. Следовательно, критерий нельзя использовать для характеристики чувствительности сенсорной системы.
Из рисунка видно, чем меньше перекрываются кривые, тем меньше вероятность ошибки. А перекрытие кривых зависит от соответствующих средних значений mn и ms и размаха изменчивости величины сенсорного эффекта вокруг этих средних. Изменчивость сенсорных эффектов характеризуется дисперсией s2. Отсюда показателем возможности обнаружения может служить величина d’, которая вычисляется по формуле:
d’ = (ms - mn)/ s,
где: ms – математическое ожидание сенсорных эффектов, вызываемых действием сигнала + шум;
mn – математическое ожидание сенсорных эффектов, вызываемых шумом:
s - стандартное отклонение;
s2 - дисперсия.
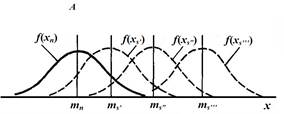
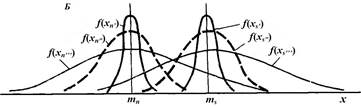 Рис. 4. Зависимость области перекрытия кривых распределения от интенсивности сигнала (А) и дисперсии (Б)
Рис. 4. Зависимость области перекрытия кривых распределения от интенсивности сигнала (А) и дисперсии (Б)
Таким образом, возможность обнаружения сигнала на фоне шума зависит не только от принятого критерия, но и от свойств шума и сигнала.
Зависимость результатов наблюдения от этих свойств выражается с помощью кривых рабочей характеристики приемника (РХП).
РХП отражает зависимость вероятности обнаружения сигнала от вероятности ложных тревог.
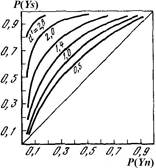
Рис. 6. Кривые РХП при разных значениях d'(по Светсу, Таннеру, Бердсоллу, 1964)
Кривая РХП получается изменением величины критерия xс. При уменьшении величины xс вероятности P (Yn) и P (Ys) увеличиваются приближаясь к 1. Когда значения xс очень маленькие любой сенсорный эффект принимается как сигнал. При больших значениях критерия вероятности P (Yn) и P (Ys)стремятся к нулю и почти каждый сенсорный эффект принимается за шум. Кривая РХП отражает изменение критерия при постоянной величине d'. Но при изменении свойств сигнала и шума величина d' меняется и получается семейство РХП.
Дата добавления: 2016-07-27; просмотров: 4853;











