Оценка для дисперсии случайной величины
В качестве оценки для дисперсии рассмотрим следующую величину:
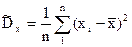 .
.
Оценку (5.2.8) принято называть выборочной дисперсией. Проверим ее на состоятельность и несмещенность. Преобразуем выражение (5.2.8) к другому виду:
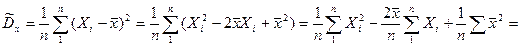
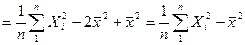 .
.
Первый член в выражении представляет собой среднее арифметическое n наблюдаемых значений случайной величины X2, значит он сходится по вероятности к MX2. Второй член 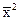 сходится по вероятности к
сходится по вероятности к 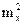 . Следовательно, правая часть сходится по вероятности к величине
. Следовательно, правая часть сходится по вероятности к величине 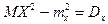 , что означает, что оценка состоятельная.
, что означает, что оценка состоятельная.
Теперь проверим, является ли выборочная дисперсия несмещенной оценкой:
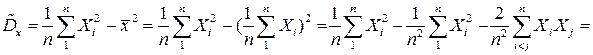
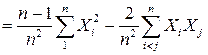 .
.
Так как дисперсия 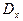 не зависит от того, в какой точке выбрать начало координат, выберем его в точке
не зависит от того, в какой точке выбрать начало координат, выберем его в точке 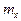 ; затем найдем математическое ожидание величины
; затем найдем математическое ожидание величины 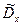 . Имеем
. Имеем 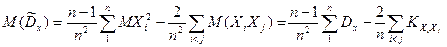 .
.
В силу независимости случайных величин  ,
, 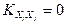 , и, следовательно,
, и, следовательно,
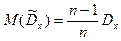 .
.
Очевидно, что выборочная дисперсия является смещенной оценкой. Однако, если умножить величину 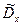 на
на 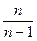 , то мы получим для дисперсии
, то мы получим для дисперсии 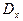 оценку, обладающую свойством несмещенности, ибо
оценку, обладающую свойством несмещенности, ибо
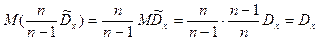 .
.
Эту оценку принято называть «исправленной» выборочной дисперсией и определять формулой
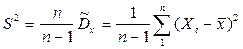 .
.
Величину  называют «исправленным» средним квадратическим отклонением. Так как множитель
называют «исправленным» средним квадратическим отклонением. Так как множитель 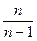 стремится к 1 при
стремится к 1 при 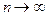 , то оценка будет также, как и
, то оценка будет также, как и 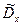 , состоятельной.
, состоятельной.
Если имеем интервальное выборочное распределение, нетрудно убедиться, что формулы для выборочной средней выборочной дисперсии и «исправленной» выборочной дисперсии можно переписать в виде
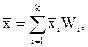
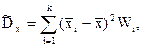
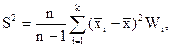
здесь 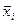 – среднее значение случайной величины X на интервале
– среднее значение случайной величины X на интервале 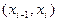 , т.е.
, т.е. 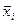 =(xi-1+xi)/2.
=(xi-1+xi)/2.
Задача. Имеется статистический ряд для случайной величины X.
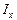
| 0-2 | 2-4 | 4-6 | 6-8 | 8-10 |
| nx |
Найти выборочную среднюю, выборочную дисперсию, «исправленную» выборочную дисперсию, «исправленное» среднее квадратическое отклонение.
Решение. Для удобства вычислений составим таблицу.
| 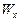
| 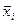 Wi Wi
| 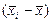
| 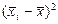
| 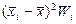
|
| 0,12 | 0,12 | -4,08 | 16,65 | 1,988 | |
| 0,16 | 0,48 | -2,08 | 4,33 | 0,693 | |
| 0,40 | 2,00 | -0,08 | 0,01 | 0,04 | |
| 0,20 | 1,40 | 1,92 | 3,69 | 0,738 | |
| 0,12 | 1,08 | 3,92 | 15,37 | 1,844 | |
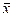 =5,08 =5,08
| 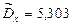
|
Значения 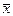 и
и 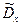 получены из таблицы Имеем
получены из таблицы Имеем 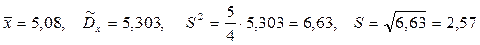 .
.
Интервальные оценки. Доверительный интервал.
Нахождение доверительных интервалов для математического ожидания и дисперсии нормального распределения случайной величины
В ряде задач требуется не только найти с помощью статистических данных точечную оценку 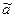 для параметра
для параметра 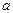 распределения, но и оценить ее точность и надежность, так как в силу случайности
распределения, но и оценить ее точность и надежность, так как в силу случайности 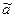 приближенная замена
приближенная замена 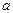 на
на 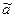 может привести к серьезным ошибкам. Для точности оценки в математической статистике используют доверительные интервалы.
может привести к серьезным ошибкам. Для точности оценки в математической статистике используют доверительные интервалы.
Пусть для параметра 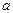 распределения случайной величины Х получена несмещенная оценка
распределения случайной величины Х получена несмещенная оценка 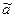 . Задаем достаточно высокую вероятность
. Задаем достаточно высокую вероятность 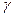 (например,
(например, 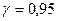 ) и находим такое значение e > 0, для которого
) и находим такое значение e > 0, для которого
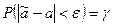 .
.
Равенство можно переписать в другом виде
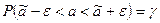 .
.
Последнее равенство можно истолковать следующим образом: неизвестное значение параметра а с вероятностью 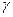 попадает в интервал
попадает в интервал 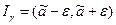 .
.
Но так как неизвестное значение параметра 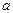 является неслучайной величиной, оценка
является неслучайной величиной, оценка 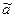 этого параметра – случайной, то равенство можно истолковать более точно следующим образом: интервал
этого параметра – случайной, то равенство можно истолковать более точно следующим образом: интервал 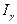 с высокой вероятностью
с высокой вероятностью 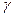 покрывает неизвестный параметр
покрывает неизвестный параметр 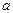 .
.
Интервал 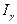 называется доверительным интервалом; центр его находится в точке
называется доверительным интервалом; центр его находится в точке 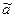 , радиус его e. Вероятность
, радиус его e. Вероятность 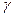 называется доверительной вероятностью или надежностью.
называется доверительной вероятностью или надежностью.
Итак, доверительный интервал 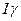 – это интервал с центром в точке
– это интервал с центром в точке 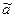 и радиусом e, который с высокой вероятностью (надежностью) покрывает неизвестный параметр
и радиусом e, который с высокой вероятностью (надежностью) покрывает неизвестный параметр 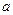 . Найти доверительный интервал – это значит по статистическим данным найти центр интервала
. Найти доверительный интервал – это значит по статистическим данным найти центр интервала 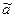 и радиус его e> 0.
и радиус его e> 0.
Дата добавления: 2016-07-27; просмотров: 5430;











