Раздел 3.2 .Модель идеального вытеснения.

Рассмотрим теперь модель аппарата полного, или идеального вытеснения.

В отличие от предыдущей модели, основным постулатом этой модели является допущение о том, что в направлении потока жидкость не перемешивается, в то время как в поперечном направлении жидкость перемешана полностью. При таких допущениях жидкость в аппарате движется подобно поршню, при этом каждый последующий слой вытесняется предыдущим. Поэтому эту модель называют еще моделью поршневого потока. В англоязычной литературе эта модель называется plug flow model. Схема аппарата представлена на рис.3.2.1.

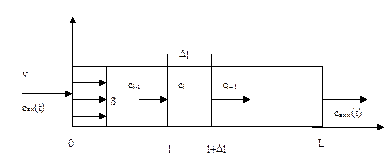
Рис.3.2.1 Схема аппарата идеального вытеснения.

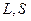– длина и площадь поперечного сечения аппарата,

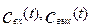- концентрация на входе и выходе из аппарата,

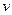- объемный расход смеси на входе и выходе из аппарата.

Выделим в аппарате элементарный объем 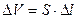и составим для него уравнение материального баланса, обозначив концентрацию в элементарном объеме через с_j, концентрацию на входе в слой через с_j-1, а концентрацию на выходе из объема через с_j+1. Накопление массы в рассматриваемом объеме будет равно интегралу от разности потоков, входящих и выходящих из рассматриваемого объема:

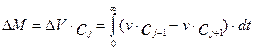(3.2.1)

Продифференцируем обе части уравнения (3.2.1) по времени и разделим на величину рассматриваемого объема 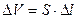. И рассмотрев предел уравнения при Dl®0, получим уравнение модели идеального вытеснения в следующем виде:

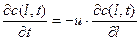(3.2.2)

Где 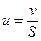- линейная скорость, м/с.

Эта модель представляет собой дифференциальное уравнение в частных производных, потому что переменная величина 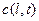изменяется в пространстве и времени. В уравнение (3.2.2) введем безразмерную пространственную координату x следующим образом: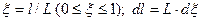

Полученное значение производной поставим в уравнение (3.2.2) и получим математическую модель в следующем виде:

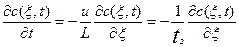(3.2.3)

Где 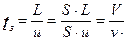- время пребывания смеси в аппарате.

Определим передаточную функцию аппарат идеального вытеснения. Для этого преобразуем уравнение (3.2.3) по Лапласу, считая x и t независимыми переменными, получим передаточную функцию модели аппарата идеального вытеснения в следующем виде:

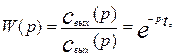(3.2.4)

Найдем реакцию модели на импульсное возмущение, т.е.

С – кривую, используя соотношение (3.1.23):

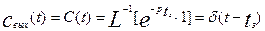(3.2.5)

Из этой формулы видно, что выходной сигнал будет повторять входной, но сдвинут на величину t_з. Аналогично можно найти выражение для F – кривой:

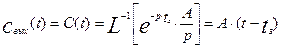(3.2.6.

На рисунках 3.2.2 и 3.2.3. показаны графики С- кривой и F – кривой:

Рис.3.2.2. Кривые отклика аппарата идеального вытеснения на импульсное возмущение, а) – изменение входной концентрации, б) изменение выходной концентрации, t_з – время пребывания смеси в аппарате

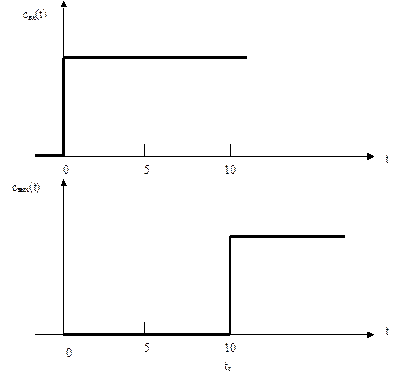
Рис.3.2.6. Кривые отклика аппарата идеального вытеснения на ступенчатое возмущение, а) – изменение входной концентрации, б) изменение выходной концентрации, t_з – время пребывания смеси в аппарате

Модель аппарата идеального вытеснения может быть использована для описания работы аппаратов, работающих по принципу вытеснения – колонные и трубчатые аппараты, теплообменники. Применение модели к описанию потоков в технологических аппаратах связывают с величиной отношения длины аппарата к его диаметру. При L/d >20 (d- диаметр аппарата) и числе Рейнольдса

Re>2300 продольное перемешивание незначительно, а турбулентное движение обеспечивает равномерно распределение концентрации по поперечному сечению аппарата. Таким образом, в этих условиях выполняются основные допущения, лежащие в основе модели идеального вытеснения.