Классификация резьб. Профиль и основные параметры метрической резьбы.
Резьбовые соединения предназначены для:
1) крепления деталей (крепежные резьбы),
2) преобразования вращательного движения в поступательное (кинематические резьбы),
3) обеспечения герметичности (трубные и арматурные резьбы),
4) решения специальных задач (специальные резьбы).
Все эти типы резьб встречаются в авиационной ракетно-космической технике. На трубных и арматурных резьбах базируется стендовое ракетно-космическое оборудование. Кинематические резьбы используются в станках, в головках различных измерительных приборов. Специальные резьбы – для телескопов, окуляров подводных лодок (окулярные резьбы), для решения трудных резьб в буровых вышках, т.е. для решения специальных задач.
В основном мы будем рассматривать крепежные резьбы, как наиболее распространенные, но надо сказать, что принципы, заложенные в стандартизацию крепежных резьб годны и для других случаев.
В зависимости от формы профиля различают:
1. треугольные,
2. трапециидальные,
3. прямоугольные,
4. круглые резьбы.
Кроме того, профиль резьбы может быть как симметричным, так и несимметричным (силовые резьбы).
В зависимости от расположения поверхности резьбы различают цилиндрические и конические резьбы, а также внутренние (гайка), наружные (болт) резьбы, от направления вращения резьбы делятся на правые и левые, от числа заходов - одно- и многозаходные резьбы.
Общим требованием для всех типов резьб является обеспечение долговечности и свинчиваемости, без подгонки независимо изготовленных резьбовых деталей.
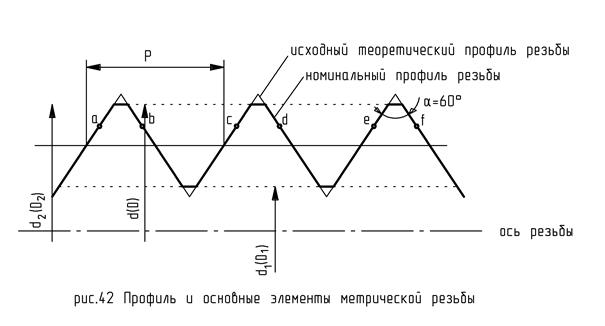
Профиль и основные элементы метрической резьбы регламентируются ГОСТом 9150-81.
Исходный теоретический профиль такой резьбы характеризуется тремя параметрами.
1) Средний диаметр болта (наружной резьбы) d2 и гайки (внутренней резьбы) D2.
Средний диаметр – диаметр воображаемого цилиндра, соосного с резьбой, образующая которого в любой осевой плоскости делится боковыми сторонами витков резьбовой поверхности на равные части.
Изобразим ось резьбы и виртуальную цилиндрическую поверхность с диаметром d2 (D2), которая разделена на равные отрезки пока еще виртуальными витками резьбы (ab=bc=cd=….). Для построения исходного теоретического профиля необходимо взять угол в 60° и опускать его до тех пор, пока он не пересечется с соответствующими точками. Таким образом, мы получим исходный теоретический профиль резьбы (рис. 44).
2) Шаг резьбы Р – расстояние между параллельными сторонами двух соседних витков резьбы, измеренное в направлении оси резьбы.
3) 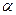 - угол профиля резьбы. Это угол между боковыми сторонами осевого профиля резьбы (для метрической резьбы
- угол профиля резьбы. Это угол между боковыми сторонами осевого профиля резьбы (для метрической резьбы 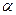 = 60º), в осевом сечении - сечения витков, соответствующие равносторонним треугольникам.
= 60º), в осевом сечении - сечения витков, соответствующие равносторонним треугольникам.
Так же кроме шага осевые размеры резьбы характеризуются ходом резьбы. Многозаходные резьбы применяются в случае соединения тонкостенных деталей, когда радиальный размер резьбы должен быть ограничен. Изобразим исходный теоретический профиль однозаходной резьбы. Для того чтобы передать примерно такие же усилия, уберем впадины и симметрично им создаем выступы. Резьба будет обладать большей прочностью при тех же осевых усилиях.
Номинальный профиль резьбы помимо указанных характеризуется дополнительно еще двумя параметрами:
4) d1 (D1) – внутренний диаметр резьбы,
5) d (D) – наружный диаметр резьбы.
Происходит подрезка теоретического профиля резьбы и номинальный профиль будет выглядеть следующим образом (рис. 42 и у этого профиля дополнительно появляются еще два диаметра.
Наружный диаметр резьбы – диаметр воображаемого цилиндра, описывающего номинальную резьбовую поверхность.
Внутренний диаметр резьбы (d1, D1) – диаметр воображаемого цилиндра вписанного в номинальную резьбовую поверхность.
Номинальная резьбовая поверхности является общей для сопрягаемых резьбовых деталей.
Осевое сечение номинальной резьбовой поверхности называется номинальным профилем.
В зависимости от соотношения между наружным диаметром резьбы и шагом различают резьбы с крупным и мелким шагом.
Если это соотношение:
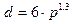 ,
,
то говорят о резьбах с крупным шагом, который в обозначении на чертежах не приводится. Указание шага необходимо для резьб с мелким шагом.
Рассмотрим обозначение резьбы:
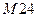
М – обозначает метрическую резьбу (α=60°);
24 – наружный диаметр d = D = 24мм.
Обозначение следует читать следующим образом: метрическая резьба с наружным диаметром 24 с крупным шагом. Если необходимо числовое значение шага, то следует посмотреть в соответствующий ГОСТ. Иногда для решения специальных задач используются резьбы с мелкими шагами и для их нарезания применяются специальные инструменты.
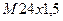
Резьба метрическая с наружным диаметром 24мм и с мелким шагом - 1,5мм.
При использовании резьб с мелким шагом увеличивается нагрузка на резьбу при меньших радиальных размерах. Это один из путей увеличения нагрузки резьбы при уменьшении радиальных габаритов, другой – увеличение заходности резьбы.
Прежде чем перейти к назначению полей допуска и посадок резьбы необходимо понять, что поскольку резьба является сложной фасонной поверхностью, характеризующейся 5 параметрами, то, по большому счету, на все параметры нужно назначить поля допуска. Особенно тяжело это сделать для шага и угла, поскольку данные параметры особенно сложно контролировать, а значит и выдерживать, поэтому в резьбовых соединениях отказались от обычной схемы назначения полей допуска. Также все параметры связаны между собой геометрически, поэтому невозможно назначать поля допуска соответствующие этим параметрам независимо друг от друга. И мы имеем право задавать поля допуска не на все эти параметры. Эти соображения и приводят нас к понятию компенсации.
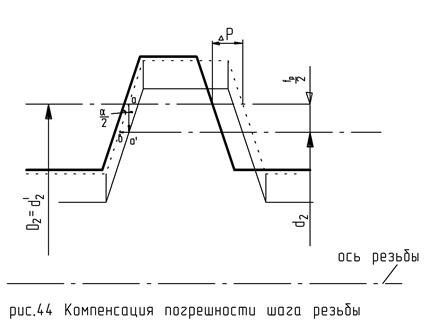
Поля допуска резьбовых деталей назначают только для диаметров, а неточности изготовления по шагу ΔΡ и по углу Δα компенсируют за счет изменения среднего диаметра резьбы. Соответственно 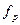 - компенсация среднего диаметра по шагу и
- компенсация среднего диаметра по шагу и 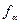 - компенсация среднего диаметра по углу α.
- компенсация среднего диаметра по углу α.
Возникает вопрос, почему мы назначаем компенсации именно по среднему диаметру резьбы, а не по наружному или внутреннему. Дело в том, что во всех резьбовых соединениях, а они бывают переходными, с натягом, с зазором (чаще с зазором), плотность свинчивания определяется только поверхностью соответствующих витков. По наружному или внутреннему диаметру во всех этих резьбах назначается зазор. Характер соединения определяется контактом по боковым поверхностям витков. И даже если в резьбовом соединении применяется посадка с натягом, по внутреннему или наружному диаметру будет зазор, поэтому компенсация назначается по среднему диаметру. По нему же назначаются и все поля допуска.
Разберемся, почему возникает погрешность изготовления по углу и шагу. При изготовлении резьбы на станке задается число оборотов и подача, и резцом нарезается резьба, также можно использовать и другие инструменты (метчики, плашки). В любом случае нарезающий инструмент изготовлен с погрешностью, погрешность имеет и ходовой винт станка и обороты станка. Погрешность может накапливаться по длине резьбы или возникать только в определенных местах. Погрешность угла профиля образуется из-за неточности угла режущего клина.
Рассмотрим пример диаметральной компенсации по среднему диаметру погрешности угла профиля α.
Пусть имеется идеальная гайка с идеальным углом профиля 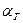 и некоторым средним диаметром
и некоторым средним диаметром 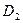 . Представим, что с идеальной гайкой мы хотим свинтить болт с таким же средним диаметром, но с погрешностью по углу профиля (рис. 46). Из рисунка видно, что если у болта такой же средний диаметр, то его профиль будет пересекаться с профилем гайки. Ясно, что свинчивание таких деталей невозможно, следовательно, должно произойти либо смятие поверхности (искажение профиля), либо отсутствие свинчивания.
. Представим, что с идеальной гайкой мы хотим свинтить болт с таким же средним диаметром, но с погрешностью по углу профиля (рис. 46). Из рисунка видно, что если у болта такой же средний диаметр, то его профиль будет пересекаться с профилем гайки. Ясно, что свинчивание таких деталей невозможно, следовательно, должно произойти либо смятие поверхности (искажение профиля), либо отсутствие свинчивания.
Компенсация проходит следующим образом, возможны два пути – уменьшение среднего диаметра болта, или увеличение среднего диаметра гайки, рассмотрим второй путь. Точку пересечения поднимем на величину диаметральной компенсации среднего диаметра. Но следует помнить о том, что с противоположной стороны, ниже оси, должна произойти такая же компенсация, поэтому компенсацию запишем, как 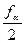 . На эту величину и поднимется вверх профиль гайки.
. На эту величину и поднимется вверх профиль гайки.
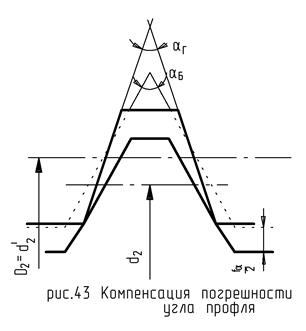
В результате этой компенсации получим профиль гайки.
Величина компенсации вычисляется из чисто геометрических соображений и приблизительно равна:
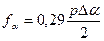 .
.
Таким образом, если с идеальной гайкой необходимо свинтить боль, имеющий только погрешность угла профиля , то при равных средних диаметрах:
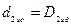
необходимо увеличить средний диаметр гайки на величину соответствующей диаметральной компенсации. 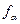 .
.
Тогда кажущийся средний диаметр такого болта:
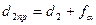 - приведенный диаметр.
- приведенный диаметр.
Аналогичным образом вводится и компенсация шага, и в общем случае приведенный диаметр болта вычисляется следующим образом:
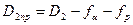 .
.
Его необходимо свинчивать с гайкой не такого же, а меньшего диаметра
Если мы изготовили болт, у которого все размеры, кроме угла, выдержаны идеально и самым точным образом измерили его средний диаметр, то его необходимо свинчивать с гайкой не такого же диаметра, а увеличенного диаметра. Несмотря на то, что геометрический диаметр болта 10 мм, то за счет компенсации для свинчивания ему необходимо 10,1 мм. Таким образом, действительный диаметр болта всегда будет больше замеренного, гайки – меньше замеренного.
Тогда при назначении допусков на средний диаметр необходимо учитывать эти компенсации, т.е. допуск должен быть увеличен на их величину.
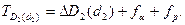
Лекция №13
Дата добавления: 2016-07-27; просмотров: 4199;











