Классификация автоколебательных систем

Любая автоколебательная система состоит из некоторого накопителя колебательной энергии (например, резонансный контур) и системы обратной связи (системы управления), которая обеспечивает подкачку энергии в систему от внешнего источника, так скажем, "в такт". По отношению накопителя к подкачке автоколебательные системы делятся на два широких класса:

1. Осцилляторные системы. В них накопитель энергии является высокодобротным контуром, а добавка энергии от внешнего источника за период колебаний много меньше, чем запас колебательной энергии системы. Это можно объяснить просто. Нам известно, что подкачка должна компенсировать потери. В установившемся режиме подкачка энергии за период в точности равна потерям. Дадим определение добротности: это отношение накопленной энергии к потерям за период. Если добротность велика, то потери за период малы в сравнении с накопленной энергией, следовательно, в осцилляторной системе и подкачка мала в сравнении с накопленной энергией. При этом, если эта подкачка является малым возбуждением, то можно ожидать, что форма колебаний в осцилляторных системах близка к синусоидальной. В этом случае амплитуда и частота колебаний определяются характеристиками системы (характеристиками накопителя) и мало зависит от системы обратной связи.

2. Релаксационные системы. Накопитель является апериодической системой, а обмен энергией накопителя с внешним источником за период колебаний сравним с запасом энергии в накопителе. Форма колебаний далека от синусоиды и сильно зависит от свойств обратной связи (например, RC мультивибратор).

В качестве знакопеременного сопротивления в автоколебательных системах могут использоваться нелинейные двухполюсники. Нелинейность может быть двух видов: N-типа и S-типа (рис. 35, 36) в зависимости от вида ВАХ нелинейного двухполюсника. Причём, как видно из ВАХ, функции двузначные, поэтому двухполюсники N-типа удобно описывать функцией, где в качестве аргумента взято напряжение, т. е. i = j(u); а S-типа описывать функцией, аргументом в которой будет ток, т. е. u = y(i).

В случае параллельного подсоединения нелинейного двухполюсника с отрицательным дифференциальным сопротивлением к параллельному контуру необходимо использовать элемент с характеристикой N-типа, показанной на рис. 35, так как общим для всех элементов такой колебательной системы является напряжение u.

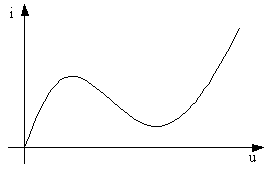Рис. 35. ВАХ нелинейного двухполюсника N-типа.

Рис. 36. ВАХ нелинейного двухполюсника S-типа.

Уравнение Кирхгофа для этой системы (рис. 37) имеет вид

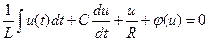
или после дифференцирования

,

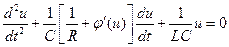(6.2)

где j'(u) = di/du - дифференциальная проводимость нелинейного элемента с падающей характеристикой, называемая также крутизной характеристики. Исследуем систему, которая описывается уравнением (6.2), на устойчивость. Для этого рассмотрим состояние равновесия u₀. Мы приложили малую амплитуду колебаний, и смотрим, будут ли они нарастать, или будут оставаться постоянными. В этой ситуации при очень малых амплитудах колебаний мы можем положить, что j'(u) » const. Характеристическое уравнение будет иметь вид

,

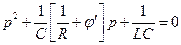решение которого

.

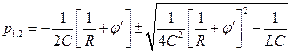Так как решение уравнения (6.2) имеет вид

,

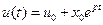то отсюда видно, что условие нарастания амплитуды колебаний следующее Re(p_1,2) > 0. Для этого нужно, чтобы, во-первых, j'(u₀) < 0 и, во-вторых, |j'(u)| > 1/R.

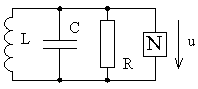Рис. 37. Схема колебательной системы с нелинейным активным элементом с характеристикой N-типа.

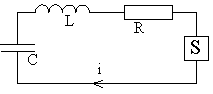Рис. 38. Схема колебательной системы с нелинейным активным элементом с характеристикой S-типа.

При последовательном соединении элементов (рис. 38) общим для всех элементов является ток i. Из правил Кирхгофа по аналогии, уже продифференцировав и разделив на L, получим уравнение движения в такой системе

.

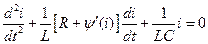(6.3)

Проверяя на устойчивость, мы получаем условие неустойчивости колебаний относительно некоторого состояния покоя i₀: y'(i₀) < 0, |y'(i₀)| > R.

Видно, что для обоих случаев первичные координаты разные (в (6.2) это напряжение u₀, в (6.3) это ток i₀), но на самом деле структура уравнений одна и та же, что в лишний раз подчёркивает изоморфизм процесса. Таким образом, уравнения (6.2) и (6.3) могут быть записаны в безразмерных обобщённых координатах и с безразмерным временем t = wt, где w² = 1/(LC) в одинаковой форме

.

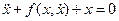(6.4)

Если функция 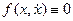, то это консервативная система (линейный осциллятор); если 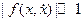, то система близка к консервативной (здесь функция в общем случае описывает и нелинейность и диссипацию). Соответственно, если система близка к линейной, т. е. имеет малую нелинейность и малую диссипацию, то она называется томпсоновской (автоколебательная система с одной степенью свободы и малыми нелинейностью и диссипацией). Малость диссипации определяется по сравнению с запасённой энергией, т. е. томпсоновская система - это частный случай осцилляторной системы.

Если, как обычно, положить 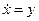, то уравнение фазовых траекторий для системы (6.4):

.

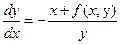(6.5)

Из физических определений известно, что если система является автоколебательной, то в ней должен существовать стационарный колебательный процесс, который на фазовой плоскости соответствует замкнутой фазовой траектории. Если автоколебания в системе устойчивы, то и замкнутая фазовая траектория также должна быть устойчива, т. е. к ней должны сходиться все фазовые траектории в близкой её окрестности. Подобные предельные фазовые траектории называют предельными циклами.

Уравнение энергетического баланса (6.1) на предельном цикле будет иметь вид

.

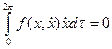Рассмотрим простейший случай, когда диссипация определяется только скоростью: f(x, y) = f(y). Пусть существует какая-то точка равновесия x = x₀, y = 0 (система, приведённая в точку равновесия с нулевой скоростью, в ней остаётся навсегда). В этой точке f(0) = 0. Вблизи равновесия функция f зависит только от y, тогда можно ожидать, что вблизи этой точки f(y) » f '(0)y. Для неустойчивости состояния покоя необходимо, чтобы f '(0)y < 0. В этом случае в системе происходит увеличение колебательной энергии. График -f(y) для автоколебательной системы с малыми потерями должен иметь вид, показанный на фазовой плоскости рис. 39.

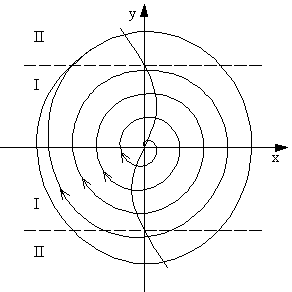Рис. 39.Фазовые траектории для томпсоновской системы.

При малых f(y) фазовые траектории напоминают окружности, а колебания в системе близки к гармоническим. Подобные автоколебательные системы принадлежат к системам томпсоновского типа. Следовательно, для томпсоновских автоколебательных систем характерна малость f(y) (|f(y)| << 1), что физически означает малую убыль и малое пополнение энергии за период колебаний в стационарном режиме. Начало координат является неустойчивой особой точкой типа фокус, и все траектории, выходящие из начала координат, через большее или меньшее число периодов колебаний (в зависимости от добротности накопительного элемента системы) приходит на предельный цикл.

В зависимости от знака f(y) вся фазовая плоскость делится на следующие области: I - инкрементная область, в которой вложение колебательной энергии превосходит потери; II - декрементные области, в которых потери превосходят вложения энергии (см. рис. 39).

Для автоколебательной системы, для которой функцию f(y) нельзя считать малой (|f(y)| ~ 1), фазовый портрет системы имеет вид, показанный на рис. 40. В такой системе колебания заметно отличаются от гармонических, процесс установления стационарных автоколебаний происходит значительно быстрее, чем в случае, показанном на рис. 39. Энергообмен в системе значительно больше, чем в системах томпсоновского типа, и выход на предельный цикл происходит примерно за период колебаний. Автоколебательная система такого типа занимает промежуточное положение между системами томпсоновского и релаксационного типов (она всё ещё осцилляторная, но уже не томпсоновская).

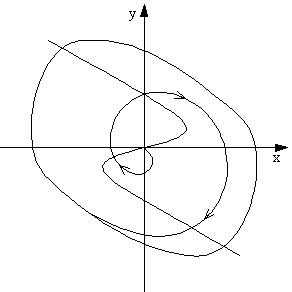Рис. 40. Вид фазовых траекторий для систем промежуточного типа.

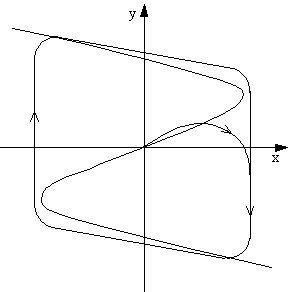Рис. 41. Вид фазовых траекторий для систем релаксационного типа.

Если мы построим на фазовой плоскости фазовые траектории для системы, у которой функция f(y) меняется в больших пределах (|f(y)| >> 1), то получим для данного вида f(y) фазовый портрет, показанный на рис. 41. Нелинейная функция f(y) такого вида соответствует автоколебательной системе релаксационного типа. Установление стационарных колебаний в подобных системах происходит практически за доли периода колебаний.

В общем случае для всех трёх систем процесс можно описать с помощью уравнения Ван дер Поля

.

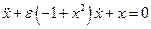(6.6)

Здесь, естественно, f(x, y) = - e(1 - x²)y. В томпсоновской системе e ~ 0.1, в промежуточной e ~ 1, в релаксационной e ~ 10.