Инерциальная нелинейность, стабилизация амплитуды

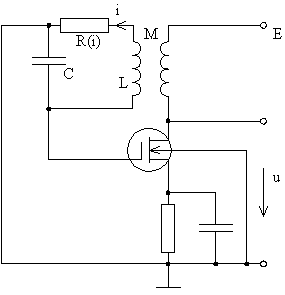Рис. 51. Генератор с термисторной стабилизацией амплитуды.

Существуют элементы, параметры которых зависят не от мгновенных значений координат, а от амплитудных значений. Такие элементы называются инерционными нелинейностями, так как они принимают соответствующие значения не сразу, а через определённое время, называемое постоянной времени того или иного элемента. Примером такой нелинейности может служить обычное сопротивление, значение которого неизбежно зависит от протекающего по нему току. В силу тепловой инерции температура, а следовательно, и сопротивление такого резисторного элемента не являются мгновенной функцией протекающего по нему тока. Эти инерционные нелинейные активные элементы называются термисторами. Рассмотрим пример, когда нелинейный элемент включен в цепь обратной связи (рис. 51). Схема

подобна схеме, изображённой на рис. 43, но теперь в резонансный контур включен термистор.

Пусть через термистор течёт синусоидальный ток i(t) = I₀cos(w₁t), тогда уравнение теплового баланса термистора принимает вид

,

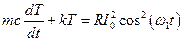(6.12)

где m - масса термистора, c - его удельная теплоёмкость, k - коэффициент теплопроводности. Решение этого уравнения имеет следующий вид:

,

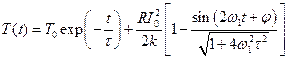(6.13)

где t = mc/k называется тепловой постоянной времени термистора, j - начальная фаза.

Из (6.13) следует, что в установившемся режиме (при t ® ¥) температуру термистора можно представить как сумму постоянной и переменной составляющих:

.

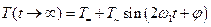Относительные пульсации температуры, т. е. отношение амплитуды переменной составляющей температуры к её постоянной составляющей, получаем из уравнения (6.13):

.

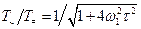Этими вариациями температуры можно пренебречь, если w₁ >> 1/t, тогда

.

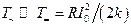Таким образом, температуру термистора можно считать практически постоянной и пропорциональной квадрату амплитуды тока через него. Следовательно, можно считать, что сопротивление термистора зависит от амплитуды тока, а не от его мгновенного значения.

Уравнение (6.8) для генератора с термисторной стабилизацией амплитуды принимает вид

,

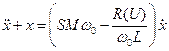(6.14)

где U - амплитуда установившихся колебаний. Соответственно, условие установившегося режима (6.9) можно переписать в виде:

.

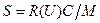(6.15)