Оцінки вартості потенціалу підприємства

Оцінка вартості потенціалу підприємства безпосередньо пов'язана з теорією зміни вартості грошей у часі, тому що:

• по-перше, існує певний часовий лаг між моментом вкладання коштів у підприємство як, об'єкт оцінки та моментом отримання доходів від користування ним як товаром;

• по-друге, існування такого часового лагу обумовлює необхідність урахування як інфляційних очікувань, так і ризику неотримання прогнозованих доходів.

Тому для нівелювання впливу фактору часу та забезпечення порівнянності вартісних показників, які прогнозуються на різні моменти часу, в теорії зміни вартості грошей застосовується часова оцінка грошових потоків. Процедура проведення такої оцінки ґрунтується на певних припущеннях:

• грошовий потік - це грошові суми, що виникають в певній хронологічній послідовності;

• грошовий потік, в якому всі суми розрізняються за величиною, називають звичайним грошовим потоком;

• грошовий потік, в якому всі суми рівновеликі та виникають через однакові проміжки часу, називають аннуітетом;

• грошовий потік може виникати наприкінці, на початку та в середині періоду;

• дохід, одержуваний на інвестований капітал, з господарського обороту не вилучається, а приєднується до основного капіталу;

• часова оцінка грошових потоків враховує ризики, пов'язані з інвестуванням;

• ризик - це вірогідність отримання в майбутньому доходу, що співпадає з прогнозною величиною;

• ставка доходу на інвестиції - це процентне співвідношення між чистим доходом і вкладеним капіталом.

Часова оцінка грошових потоків передбачає використання шести стандартних функцій складного процента, або шести функцій грошової одиниці:

1) майбутня вартість одиниці (складний процент);

2) поточна вартість одиниці (дисконтування);

3) поточна вартість аннуітета;

4) періодичний внесок на погашення кредиту;

5) майбутня вартість аннуітета;

6) періодичний внесок до фонду накопичення.

Для полегшення розрахунків в процесі оцінки грошових потоків із визначеними характеристиками (проценту ставка і період нарахування процентів) в оцінній практиці застосовують так звані фінансові таблиці (додаток 1).

1. Майбутня вартість одиниці (складний процент).

Розрахунки майбутньої вартості здійснюються за формулою:

FV = PV (l + r)ⁿ,

де FV - майбутня вартість;

PV - первинний внесок (поточна вартість);

r - процентна ставка (ставка дисконту);

n - число періодів нарахування процентів.

Множник (1 + r)ⁿ називають фактором майбутньої вартості або фактором накопичення. Його значення для різних г та п містяться в колонці 2 фінансових таблиць додатку 1.

Дана функція дозволяє визначити майбутню вартість суми, яку має інвестор сьогодні, виходячи із ставки процента, терміну накопичення та періодичності нарахування процентів, що передбачаються.

Логіка розрахунків майбутньої вартості наведена на рис. 5.1.

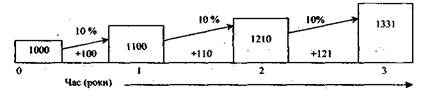
Рис. 5.1. Зростання основної суми за функцією майбутньої вартості

Таким чином, використання даної функції передбачає нарахування процентів не тільки на суму первинного внеску, але і на суму процентів, які накопичуються наприкінці кожного періоду. Це можливо тільки за умов реінвестування нарахованих процентів, що збільшує суму основного капіталу.

2. Поточна вартість одиниці (дисконтування).

Поточна вартість одиниці є зворотною величиною відносно майбутньої вартості, тому процес її визначення називають дисконтуванням, а її розрахунки для суми FV ведуться за формулою:

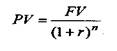
Величину 1/(1+r)ⁿ називають дисконтним множником або фактором поточної вартості. Його значення для різних r та n містяться в кол.3 фінансових таблиць додатку 1.

Дана функція надає можливість визначити теперішню вартість суми, якщо відома її майбутня величина, період, за який цю суму накопичено, та процента ставка. Графічна інтерпретація функції дисконтування наведена на рис. 5.2.

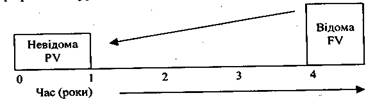Рис. 52. Поточна вартість одиниці

3. Поточна вартість аннуітету.

Оскільки аннуітет становить собою особливий грошовий потік, представлений однаковими сумами через однакові часові інтервали, то відносно інвестора він може бути як вихідним (наприклад, здійснення періодичних однакових платежів), так і вхідним грошовим потоком (наприклад, регулярні надходження фіксованих сум орендної плати).

Крім того, залежно від моменту здійснення першого аннуітетного платежу розрізняють звичайний та авансовий аннуітет. Звичайний аннуітет визначається як сума рівновеликих платежів, що здійснюються наприкінці періоду. Авансовий аннуітет має місце за умов часового збігу першого платежу з депонуванням основної суми внеску.

Графічна інтерпретація поточної вартості звичайного аннуітету наведена на рис. 5.3

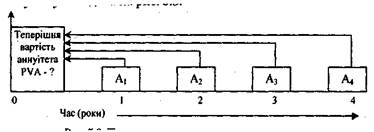5.3. Поточна вартість звичайного аннуітету

Формула для розрахунку звичайного аннуітету має вигляд:

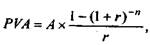
де PVA - поточна вартість аннуітету; А - платіж n-го періоду.

Множник 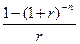називають дисконтним множником аннуітету, фактором поточної вартості аннуітету або фактором Інвуда. Його значення для різних r та n містяться в кол. 4 фінансових таблиць додатку 1.

Графічна інтерпретація поточної вартості авансового аннуітету наведена на рис. 5.4:

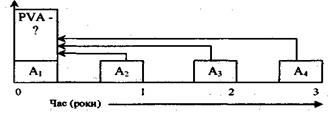Рис. 5.4. Поточна вартість авансового аннуітету

Для того, щоб розрахувати поточну вартість авансового аннуітету, необхідно дослідити рух грошового потоку. Оскільки перший платіж збігається за часом із депонуванням основної Суми внеску, то його майбутня вартість дорівнює теперішній і не потребує дисконтування для забезпечення порівнянності. Всі наступні аннуітетні платежі дисконтуються в звичайному порядку, проте період дисконтування завжди буде на одиницю менше. Тому фактор поточної вартості авансового аннуітету дорівнює фактору поточної вартості звичайного аннуітету для попереднього періоду, збільшеному на одиницю.

Формула для розрахунку авансового аннуітету має вигляд:

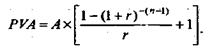
Зміни, що відбуваються у зовнішньому середовищі, а також розвиток внутрішнього потенціалу підприємства чинять суттєвий вплив на величину періодичного Грошового потоку доходів. Тому на практиці досить часто трапляються ситуації, коли за визначений розрахунковий період величина періодичних платежів змінюється, що вимагає застосування певних методичних прийомів розрахунку поточної вартості таких аннуітетних платежів.

4. Періодичний внесок на погашення позики (внесок на амортизацію одиниці)

Ця функція виступає зворотною відносно поточної вартості аннуітету і використовується для розрахунку фіксованої суми аннуітетного платежу, якщо відомі його поточна вартість, кількість внесків і ставка дисконту. Під амортизацією в даному Випадку розуміють процес погашення боргу за визначений період часу.

Графічна інтерпретація розрахунків періодичного внеску на погашення позики наведена на рис. 5.8.

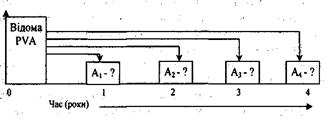Рис.5.8. Періодичний внесок на погашення позики

Розрахунок періодичного внеску на погашення позики (амортизацію одиниці) здійснюється за формулою: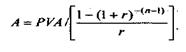

Множник 1/ [(1-(1+r)^-(ⁿ^-1))/r] називається фактором внеску на амортизацію одиниці або фактором внеску на погашення позики. Його значення для різних r та n містяться в кол. 5 фінансових таблиць додатку 1.

5. Майбутня вартість аннуітету (зростання одиниці за період)

Використання цієї функції доцільно за умов визначення майбутньої вартості суми, яку буде накопичено за рахунок надходження аниуітетних платежів при заданій процентній ставці (рис. 5.9).

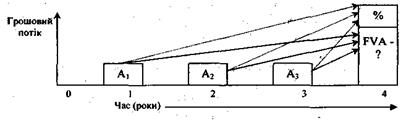Рис. 5.9 Майбутня вартість аннуітету

Розрахунок майбутньої вартості звичайного аннуітету здійснюється за формулою:

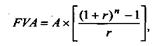
де FVA - майбутня вартість аннуітету.

Множник ((1+r)ⁿ - 1)/r називається фактором майбутньої вартості аннуітету. Його значення для різних r та n містяться в кол. 6 фінансових таблиць додатку 1.

Для авансового аянуітєту розрахункова формула майбутньої вартості має вигляд:

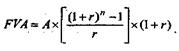
6. Періодичний внесок до фонду нагромадження (фактор фонду відшкодування).

Дана функція є зворотною відносно майбутньої вартості аннуітету та дозволяє визначити розмір грошового внеску, який .слід періодично депонувати на рахунок, щоб^-через певний часу мати необхідну суму .коштів, при заданій ставці дисконту (рис. 5.10).

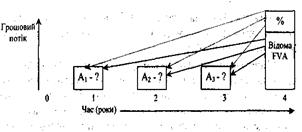Рис. 5.10. Періодичний внесок до фонду нагромадження

Формула для розрахунку періодичного внеску до фонду нагромадження має вигляд:

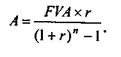
Множник r/((1+r)ⁿ - 1) називається фактором періодичного внеску до фонду нагромадження або фактором внеску до фонду відшкодування. Його значення для різних r та n містяться в кол. 7 фінансових таблиць додатку 1.

<1 2 345 6 7 >

Дата добавления: 2020-10-25; просмотров: 358;