Комплексный коэффициент передачи и частотные характеристики

Рассмотрим случай, когда на вход системы РА действует гармонический сигнал с амплитудой X_m и частотой w:

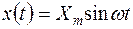. (3.22)

Сигнал на выходе системы при нулевых начальных условиях в соответствии с выражением (3.5) имеет вид

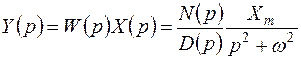, (3.23)

изображению (3.23) соответствует оригинал

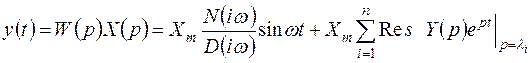. (3.24)

В устойчивой системе все полюсы имеют отрицательные вещественные части, поэтому в установившемся режиме выходной сигнал имеет вид

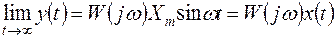, (3.25)

т.е. на выходе системы также получается гармонический сигнал, частота которого равна частоте входного сигнала.

Отношение гармонического сигнала на выходе в установившемся режиме к гармоническому сигналу на входе называют комплексным коэффициентом передачи или частотной характеристикой системы РА. Из выражения (3.25) следует, что

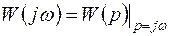. (3.26)

Частотная характеристика системы РА может быть представлена в виде

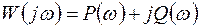, (3.27)

где 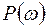– вещественная частотная характеристика; 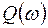– мнимая частотная характеристика.

Частотная характеристика системы РА в показательной форме имеет вид

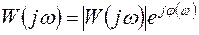, (3.28)

где 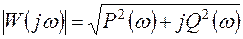– амплитудно-частотная характеристика; 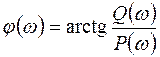– фазочастотная характеристика.

Амплитудно-частотная характеристика (АЧХ) определяет зависимость от частоты отношения амплитуды сигнала на выходе системы к амплитуде сигнала на входе. Фазочастотная характеристика (ФЧХ) устанавливает зависимость сдвига фаз между входным и выходным сигналами.

На плоскости комплексного переменного частотная характеристика изображается в виде вектора (рис. 3.3), который при изменении частоты от нуля до бесконечности описывает кривую, называемую амплитудно-фазовой характеристикой или годографом частотной характеристики системы РА.

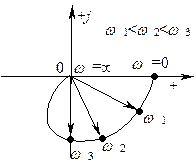
Рис. 3.3 - Годограф частотной характеристики системы РА

В инженерной практике применяют логарифмические амплитудно-частотные характеристики (ЛАЧХ). Логарифмическая АЧХ имеет зависимость

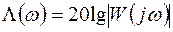. (3.29)

При построении ЛАЧХ (рис. 3.4) по оси ординат откладывают значение (3.29) в децибелах, а по оси абсцисс – частота w в логарифмическом масштабе.

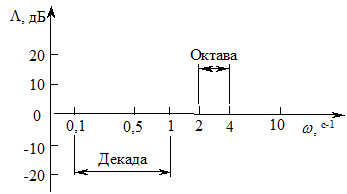
Рис. 3.4 - К описанию логарифмической частотной характеристики

При построении логарифмической ФЧХ по оси ординат откладывают ее значение в радианах, используя десятикратное изменение частоты, называемой изменением на декаду, а двукратное – изменением на октаву. В ряде случаев возможно пренебрежение кривизной ЛАЧХ на небольших участках частот, поэтому построение ЛАЧХ производится отрезками прямых линий – асимптотами. Основным достоинством ЛАЧХ является возможность их построения без вычислений.

Наиболее характерный вид имеют ЛАЧХ при следующих значениях модуля L(w) частотной передаточной функции:

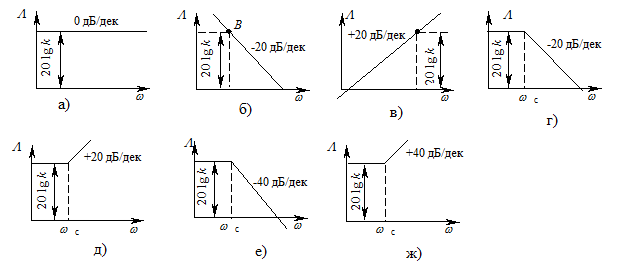Рис. 3.5 - Типовые асимптотические ЛАЧХ

а) L = k. В этом случае L = 20 lg k есть постоянная величина и ЛАЧХ представляет собой прямую, параллельную оси абсцисс (рис. 3.5, а);

б) 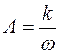. В этом случае L = 20 lg k – 20 lg w. При w = 1 имеем L = 20 lg k и на протяжении одной декады (с увеличением w в 10 раз) L уменьшается на 20 дБ. ЛАЧХ представляет собой прямую с наклоном –20 дБ/дек, проходящую через точку B с координатами [1; 20 lg k] (рис. 3.5, б).

в) L = kw. В этом случае L = 20 lg k + 20 lg w. При w = 1 имеем L = 20 lg k и на протяжении одной декады (с увеличением w в 10 раз) L увеличивается на 20 дБ. ЛАЧХ представляет собой прямую с наклоном +20 дБ/дек, проходящую через точку B с координатами [1; 20 lg k] (рис. 3.5, в).

г) 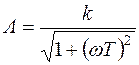. В этом случае L = 20 lg k –10 lg (1+w² T²). При малых частотах w²T² << 1 и L » 20 lg k. Это низкочастотная асимптота, параллельная оси абсцисс. При больших частотах w²T² >> 1 и L » 20 lg k –10 lg w T. Это высокочастотная асимптота с отрицательным наклоном 20 дБ/дек. Следовательно, асимптотическая ЛАЧХ образуется двумя асимптотами, которые сопрягаются при частоте 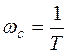(рис. 3.5, г), так как при этой частоте удовлетворяются уравнения обеих асимптот.

д) 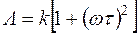. В этом случае L = 20 lg k +10 lg (1+w² t²). ЛАЧХ образуется двумя асимптотами, которые сопрягаются на частоте 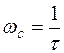, но высокочастотная асимптота имеет положительный наклон +20 дБ/дек (рис. 3.5, д).

е) 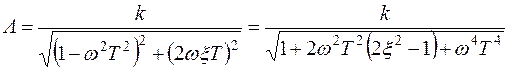, где x <1. В данном случае L = 20 lg k – 10 lg [1+2w² T² (2x² – 1) + +w⁴ T⁴]. На малых частотах L » 20 lg k и на высоких частотах L » 20 lg k –40 lg wT. Асимптотическая ЛАЧХ, как и в двух предыдущих случаях, составляется двумя асимптотами, которые сопрягаются при частоте w_с = 1/Т. Низкочастотная асимптота параллельна оси абсцисс, а высокочастотная имеет наклон минус 40 дБ/дек (рис. 3.5, е).

ж) 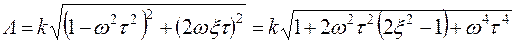, где x <1. В этом случае L = 20 lg k + 10 lg [1+2w² t² (2x² – 1) + w⁴ t⁴]. Асимптотическая ЛАЧХ составляется двумя асимптотами, которые сопрягаются при частоте w_с = 1/t. Низкочастотная асимптота L » 20 lg k параллельна оси абсцисс, а высокочастотная имеет наклон + 40 дБ/дек (рис. 3.5, ж).