Проблема моделирования элементов систем радиоавтоматики

Исходными уравнениями для анализа систем РА являются дифференциальные уравнения ее элементов, которые составляются на основании их принципов работы. В большинстве случаев эти уравнения оказываются нелинейными, что усложняет анализ систем. Поэтому всегда, когда это можно, стремятся провести линеаризацию характеристик нелинейных устройств. Линеаризацию производят по формуле Тейлора, в соответствии с которой разложение нелинейной функции двух аргументов имеет вид

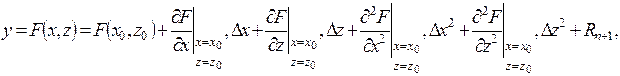(4.1)

где x₀, z₀ – постоянные установившихся значений, входных параметров переменных x и z; Dx, Dz – малые отклонения от установившихся значений x и z; R_n+1 – остаточный член.

При работе устройств в составе системы РА отклонения Dx и Dz малы, поэтому в выражении (4.1) можно ограничиться только первыми порядками отклонений этих переменных. В этом случае из (4.1) следует, что приращение выходного сигнала определяется как

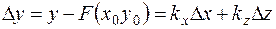, (4.2)

где 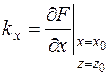; 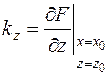– коэффициенты передачи.

Выражение (4.2) и является линеаризованным уравнением элементов систем РА. В общем случае это уравнение содержит не только отклонения переменных, но и их производные, т.е. в результате линеаризации получается дифференциальное уравнение, преобразование Лапласа которого определяет передаточную функцию линеаризованных элементов системы РА.

Далее рассматриваются уравнения основных устройств системы РА и определяются их передаточные функции.