Передаточная функция систем радиоавтоматики

Применив к дифференциальному уравнению (3.1) преобразование Лапласа, получим

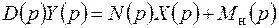, (3.3)

где ;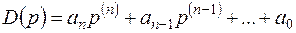

;

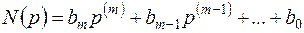Y(p) – преобразование Лапласа для выходного сигнала;

X(p) – преобразование Лапласа для входного сигнала системы;

M_н – многочлен, отображающий начальные условия.

Введя следующие обозначения, получим:

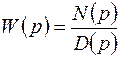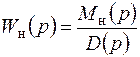; . (3.4)

Тогда выражение (3.3) примет вид

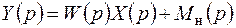. (3.5)

Это уравнение связывает изображение выходного сигнала системы. Функция W(p) характеризует динамические свойства системы РА, она не зависит от управляющего воздействия и полностью определяется параметрами системы a_i и b_i. Эту функцию называют передаточной, а W_н(p) – передаточной функцией относительно начального состояния системы РА.

При нулевых начальных условиях передаточная функция системы РА равна отношению изображения по Лапласу выходного сигнала к преобразованию Лапласа входного сигнала. Передаточная функция является дробно рациональной функцией относительно оператора преобразования Лапласа

. (3.6)

Степень полинома знаменателя передаточной функции определяет порядок системы РА. В реальных системах степень полинома числителя передаточной функции не превышает степени полинома знаменателя. Это условие называется физической реализуемостью системы РА; оно означает, что нельзя создать систему РА, передаточная функция которой не удовлетворяла бы этому условию.

Корни полинома числителя передаточной функции b_i называются нулями, а корни знаменателя l_i – полюсами системы РА. Так как коэффициенты передаточной функции – действительные числа, то невещественные нули и полюсы могут быть только комплексно-сопряженными величинами. При анализе систем РА нули и полюсы (особенности передаточной функции) удобно изображать точками на плоскости комплексного переменного p (рис. 3.1).

Рис. 3.1 - Расположение нулей и полюсов передаточной функции

на плоскости комплексного переменного

Если передаточная функция системы не содержит особенностей в правой части плоскости p, то систему называют минимально-фазовой, в противном случае ее считают неминимально-фазовой.