Типовые примеры и методы их решения

Пример 1.1.1. Предприниматель получил на полтора года кредит в размере 40 тыс. руб. с условием возврата 50 тыс. руб. Определите процентную ставку, учетную ставку и дисконт-фактор за полтора года. Чему равен индекс роста суммы кредита?

Решение. Полагая в формуле (1) (см. приложение 1) t = 1,5 года, РV =40 тыс. руб., FV = 50 тыс. руб., получим величину процентной ставки за полтора года:

r_1,5= 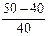= 0,25, или, что равносильно, r_1,5 = 25% .

Аналогичным образом учетную ставку и дисконт-фактор находим соответственно по формулам (2),(4):

d_l,5 = 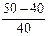= 0,2 или d_1,5 = 20%;

v_1,5 = 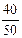=0,8 или v_1,.5 = 80%

Заметим, что величины d_{l. 5}, v_1..5 можно было найти, используя и другие соотношения. Например,

d_{l, 5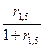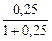}= _{= =0,2}

v_1.,5=1-d_1,5=1-0,2=0,8

Индекс роста В_1,5 суммы кредита показывает, во сколько раз возвращаемая сумма больше выданной:

B_1,5= 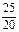=1,25.

Пример 1.1.2. Известно, что капитал, помещенный в банк, вырос за первый год в 1,4 раза, а за второй год вся сумма увеличилась в 1,2 раза. Определите индекс роста вклада и процентную ставку за два года. На сколько процентов увеличился капитал за все время?

Решение. Индекс роста капитала В_1,5 за два года находим перемножением индексов роста за каждый год:

B₂=1,4 ^. 1,2=1,68.

Следовательно, двухгодовая процентная ставка, показывающая, на сколько процентов увеличится капитал, составит:

r₂ = B₂– 1= 1,68 – 1=0,68.

Таким образом, капитал за два года увеличится на 68%.

Пример 1.1.3. Имеется два варианта вложения капитала на 3 года. Согласно первому варианту исходный капитал за первый год увеличится на 15%, за второй год вся сумма увеличится на 35%, а за третий год - еще на 10%. Для второго варианта рост капитала составит каждый год 20% от суммы предыдущего года. Какой вариант лучше?

Решение. Поскольку для первого варианта индексы роста капитала за каждый год равны 1,15; 1,35 и 1,1, то индекс роста за 3 года составит:

1,15 ^. 1,35 ^. 1,1 =1,70775 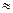1,708 .

Подобным образом находим индекс роста капитала за 3 года для второго варианта:

1,2 ^. 1,2 ^. 1,2 =1,728.

Так как согласно первому варианту за 3 года капитал увеличится на 70,8%, а согласно второму варианту - на 72,8%, то второй вариант вложения капитала лучше.

Заметим, что 70,8% и 72,8% представляют собой процентные ставки за 3 года.

Пример 1.1.4. Определите доходность в виде процентной ставки за предоставление потребительского кредита на следующих условиях: 45% стоимости покупок оплачивается сразу, а через год вносится оставшаяся часть стоимости покупок и 10% от стоимости покупок в качестве платы за кредит.

Решение. Воспользуемся формулой (1). Обозначим через Р стоимость покупок. Поскольку 45% стоимости покупок оплачивается сразу, то на один год кредит предоставляется в размере PV = 0,55P. Величина дохода за предоставленный кредит составит FV-PV = 0,1P . Поэтому

r₁= 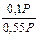=0,1818, или =18,18%.

Пример 1.1.5. Найдите с 90 тыс. руб.: а) 15% "со 100"; б) 15% "на100"; в) 15% "во 100".

Решение. Выражая 15% в десятичных дробях (т.е. получая 0,15), пользуемся последовательно формулами (6), (7), (8) при r=0,15 u Q=S=K=90 тыс. руб.:

a) 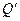= 90 ^. 0,15 =13,5 тыс. руб.;

6) 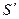= = 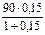11,739 тыс. руб.;

в) 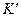= =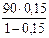15,882 тыс. руб.

Получили, что по отношению к одному числу проценты "на 100" меньше процентов "со 100", которые в свою очередь меньше процентов "во 100".

Для проверки найденных процентов "на 100" надо из данного числа (90 тыс. руб.) вычесть полученные проценты "на 100" (11,739 тыс. руб.), определив тем самым так называемое начальное число. Затем от начального числа найти проценты "со 100 ", которые должны совпадать с найденными согласно условию задачи процентами "на 100". Выполним эти действия:

90 – 11,739 = 78,261 тыс. руб.;

78,261^. 0,15= 11,739 тыс. руб.

Для проверки найденных процентов "во 100" надо к данному числу (90 тыс. руб.) прибавить полученные проценты "во 100" (15,882 тыс. руб.) и затем от найденной суммы (т.е. начального числа 105,882 тыс. руб.) найти проценты "со 100 ":

90 + 15,882 = 105,882 тыс. руб.;

105,882 ^. 0,5 = 15,882 тыс. руб.

Пример 1.1.6. Предприниматель реализовал партию товара за 80 тыс. руб., получив при этом 25% прибыли. Определите величину прибыли и себестоимость товара.

Решение. Поскольку 80 тыс. руб. представляют собой сумму себестоимости товара и процентов "со 700" этой себестоимости (прибыли), то величина прибыли определяется по формуле (7) вычисления процентов "на 100". Полагая S=80 тыс. руб., r = 0,25, находим:

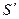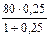= =16 тыс. руб.

Следовательно, себестоимость товара составляет 80 - 16 = 64 тыс.руб.

Пример 1.1.7. Предприниматель реализовал партию товара за 57 тыс. руб., получив при этом 5% убытка. Определите величину убытка и себестоимость товара.

Решение. Поскольку 57 тыс. руб. представляют собой разность себестоимости товара и процентов "со /00" этой себестоимости (убытка), то величина убытка определяется по формуле (8) вычисления процентов "во /00" при К = 57 тыс. руб. и r = 0,05:

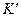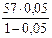= = 3 тыс. руб.

Следовательно, себестоимость товара составляет 57 + 3 = 60 тыс. руб.

Из разобранных двух последних примеров видно, что при применении формул вычисления процентов "на 100" или "во 100" (формулы (7) и (8)) вначале нужно определить, с каким капиталом (согласно условию задачи) имеем дело - с наращенным или уменьшенным, после чего решение задачи не представляет трудностей.